Betti cohomology provides a powerful tool to study the topological properties of spaces by linking algebraic invariants to geometric structures. It captures essential information about the number of holes or connected components, offering insight into the shape and connectivity of a space. Discover how Betti cohomology can deepen Your understanding of complex topological phenomena by exploring the full article.
Table of Comparison
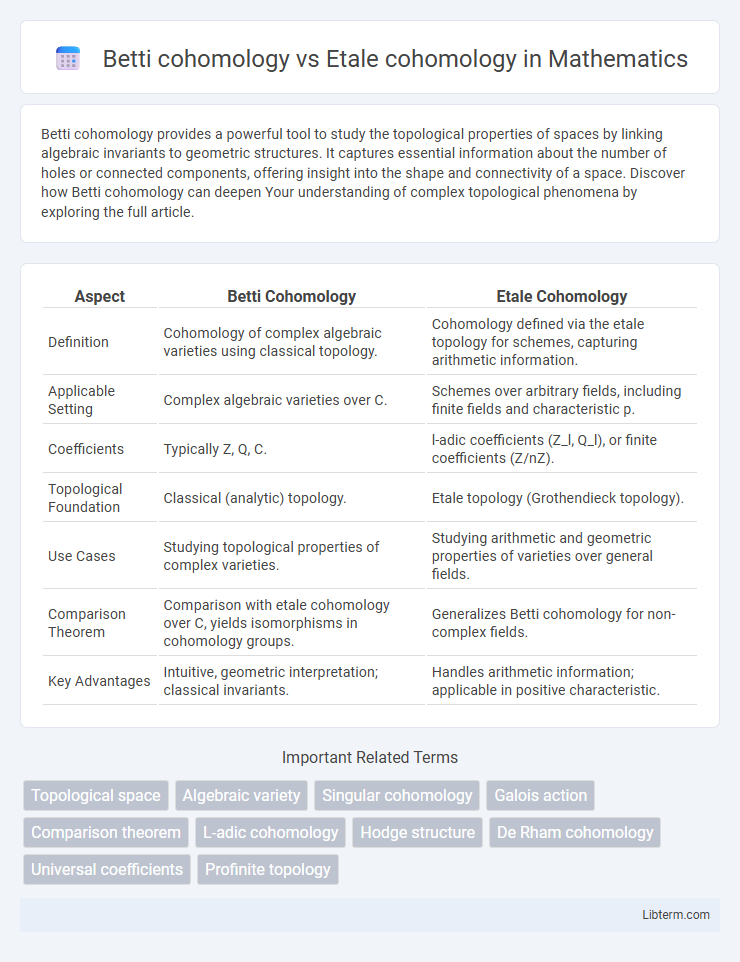
| Aspect | Betti Cohomology | Etale Cohomology |
|---|---|---|
| Definition | Cohomology of complex algebraic varieties using classical topology. | Cohomology defined via the etale topology for schemes, capturing arithmetic information. |
| Applicable Setting | Complex algebraic varieties over C. | Schemes over arbitrary fields, including finite fields and characteristic p. |
| Coefficients | Typically Z, Q, C. | l-adic coefficients (Z_l, Q_l), or finite coefficients (Z/nZ). |
| Topological Foundation | Classical (analytic) topology. | Etale topology (Grothendieck topology). |
| Use Cases | Studying topological properties of complex varieties. | Studying arithmetic and geometric properties of varieties over general fields. |
| Comparison Theorem | Comparison with etale cohomology over C, yields isomorphisms in cohomology groups. | Generalizes Betti cohomology for non-complex fields. |
| Key Advantages | Intuitive, geometric interpretation; classical invariants. | Handles arithmetic information; applicable in positive characteristic. |
Introduction to Betti and Étale Cohomology
Betti cohomology is a topological invariant derived from singular cohomology of complex algebraic varieties, capturing the shape and holes of complex manifolds using continuous maps to simplicial complexes. Etale cohomology, developed to overcome limitations of singular cohomology in algebraic geometry, uses the etale topology to study algebraic varieties over arbitrary fields, especially in characteristic p and arithmetic contexts. Both cohomologies provide tools for understanding algebraic structures, with Betti cohomology linking geometry over the complex numbers and etale cohomology enabling arithmetic and etale fundamental group analyses.
Historical Background and Motivations
Betti cohomology originated from the study of topological invariants of complex algebraic varieties, building on the work of Enrico Betti in the late 19th century who introduced Betti numbers to describe holes in topological spaces. Etale cohomology was developed by Alexander Grothendieck in the 1960s as a response to the limitations of classical cohomology theories over non-algebraically closed fields, aiming to define a cohomology theory that could handle arithmetic varieties and support the proof of the Weil conjectures. The motivation for etale cohomology was to create a tool analogous to singular cohomology but applicable in algebraic geometry, particularly over fields with nontrivial Galois groups, integrating both geometric and arithmetic information.
Fundamental Definitions and Concepts
Betti cohomology arises from the singular cohomology of complex algebraic varieties viewed as topological spaces, capturing topological invariants using continuous maps and simplicial complexes. Etale cohomology, defined via the etale topology on algebraic varieties, uses sheaf theory to handle fields lacking analytic structure, providing tools to study arithmetic properties through Galois actions. The fundamental distinction lies in Betti cohomology relying on classical topological methods, while etale cohomology extends these ideas algebraically to schemes, enabling insights into number theory and algebraic geometry.
Underlying Topologies: Classical vs. Étale
Betti cohomology is based on the classical topology of complex algebraic varieties, utilizing continuous maps and singular homology to capture topological information. Etale cohomology arises from the etale topology, a Grothendieck topology designed to handle algebraic varieties over arbitrary fields, allowing the study of algebraic structures via sheaves on the etale site. The fundamental difference lies in Betti cohomology's reliance on classical analytic spaces versus etale cohomology's use of a more flexible, algebraically defined etale topology, enabling insights into arithmetic and geometric properties beyond the complex case.
Comparison for Complex Algebraic Varieties
Betti cohomology and etale cohomology both serve as fundamental tools for studying complex algebraic varieties, with Betti cohomology arising from the classical topology of the associated complex analytic space, while etale cohomology provides a more algebraic and arithmetic framework applicable even over fields other than \(\mathbb{C}\). Betti cohomology groups \(H^n_{B}(X, \mathbb{Z})\) are computed using singular cohomology on the complex manifold \(X(\mathbb{C})\), capturing topological invariants, whereas etale cohomology groups \(H^n_{\text{et}}(X, \mathbb{Z}_\ell)\) involve limits over finite covers respecting the etale topology and link Galois actions to geometric structure. Comparison theorems such as the Artin comparison theorem establish isomorphisms \(H^n_B(X, \mathbb{Z}_\ell) \cong H^n_{\text{et}}(X, \mathbb{Z}_\ell)\) for complex varieties, enabling a translation between topological and algebraic data pivotal for understanding the interplay between geometric intuition and arithmetic properties.
Key Differences in Algebraic-Geometric Contexts
Betti cohomology, derived from the topological space of complex algebraic varieties, captures topological invariants using singular cohomology with classical topology, making it suitable for complex manifolds. Etale cohomology generalizes this concept over arbitrary fields by employing the etale topology, allowing for the study of algebraic varieties in a broader arithmetic and geometric context, including those over finite fields. Key differences include Betti cohomology's reliance on classical topology and complex points, while etale cohomology uses etale covers to manage algebraic and arithmetic properties, crucial for formulating Grothendieck's Weil conjectures and understanding Galois actions.
Role in the Weil Conjectures and Number Theory
Betti cohomology provides topological invariants of complex algebraic varieties, enabling the interpretation of geometric properties through singular cohomology with complex coefficients. Etale cohomology extends these concepts to schemes over finite fields, crucially providing l-adic cohomology groups that satisfy the necessary properties for proving the Weil Conjectures, including the analog of the Lefschetz fixed point formula and the rationality and integrality of zeta functions. In number theory, etale cohomology plays a foundational role in connecting algebraic geometry to Galois representations and in formulating deep results such as the proof of the Weil Conjectures by Deligne.
Applications in Modern Algebraic Geometry
Betti cohomology, based on classical topology, provides a powerful tool for studying the topological properties of complex algebraic varieties, enabling computations of invariants such as Betti numbers that classify their shape. Etale cohomology, adapted for algebraic varieties over arbitrary fields, plays a crucial role in arithmetic geometry and the proof of the Weil conjectures by offering a cohomology theory compatible with finite field extensions and Galois actions. Both theories intersect in the comparison theorem, allowing the transfer of topological intuition to arithmetic contexts and underpinning modern developments in the Langlands program and the study of motives.
Limitations and Challenges of Each Theory
Betti cohomology faces limitations in dealing with varieties over fields other than the complex numbers, restricting its applicability to analytic topology and complex algebraic geometry. Etale cohomology, while powerful for arithmetic and algebraic applications, encounters challenges such as complicated Galois actions and technical difficulties in defining coefficients, especially in characteristic p settings. Both theories struggle with computational complexity in higher dimensions and require sophisticated machinery to bridge topological and arithmetic information effectively.
Summary: Choosing Between Betti and Étale Cohomology
Betti cohomology applies naturally to complex algebraic varieties by leveraging their underlying topological spaces, providing insights aligned with classical topology. Etale cohomology extends cohomological methods to algebraic varieties over arbitrary fields, particularly useful for understanding arithmetic properties and Galois actions. Selecting between Betti and etale cohomology depends on the base field and geometric context: Betti cohomology is ideal for complex varieties, while etale cohomology is essential for arithmetic geometry and fields lacking complex embeddings.
Betti cohomology Infographic
 libterm.com
libterm.com