The infimum represents the greatest lower bound of a set in mathematical analysis, defining the highest value that is less than or equal to every element in the set. Understanding the infimum is crucial for grasping concepts related to limits, optimization, and order theory. Explore the rest of the article to deepen your knowledge of how the infimum applies in various mathematical contexts.
Table of Comparison
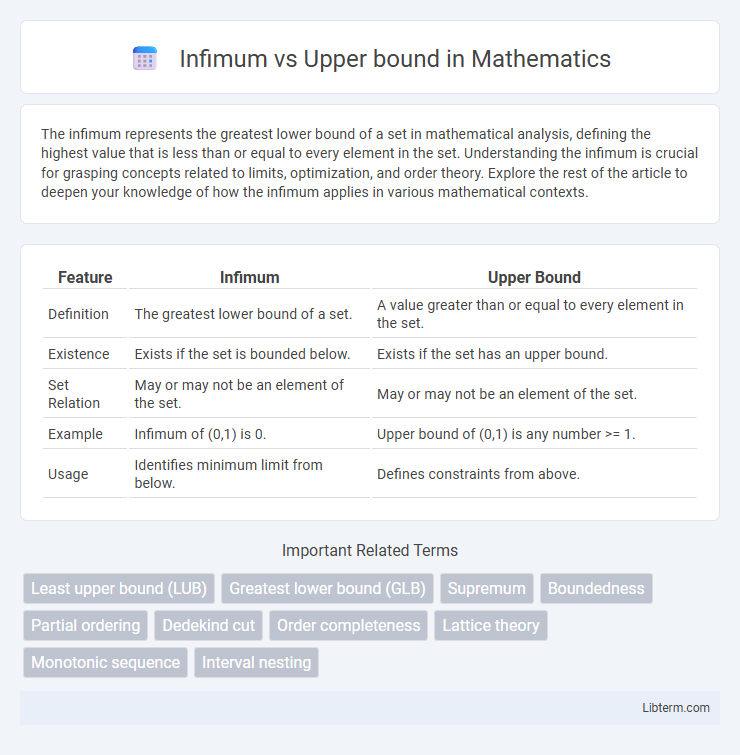
| Feature | Infimum | Upper Bound |
|---|---|---|
| Definition | The greatest lower bound of a set. | A value greater than or equal to every element in the set. |
| Existence | Exists if the set is bounded below. | Exists if the set has an upper bound. |
| Set Relation | May or may not be an element of the set. | May or may not be an element of the set. |
| Example | Infimum of (0,1) is 0. | Upper bound of (0,1) is any number >= 1. |
| Usage | Identifies minimum limit from below. | Defines constraints from above. |
Introduction to Infimum and Upper Bound
The infimum of a set is the greatest value that is less than or equal to every element in the set, often referred to as the greatest lower bound. An upper bound is any value greater than or equal to all elements within the set, representing a ceiling that contains the set from above. Understanding the relationship between infimum and upper bound is crucial in mathematical analysis, particularly in optimization and limit theory.
Key Definitions: Infimum and Upper Bound
The infimum of a set is the greatest element that is less than or equal to every element in the set, often referred to as the greatest lower bound. An upper bound of a set is any element that is greater than or equal to every element within that set, not necessarily the smallest such element. While the infimum identifies the maximal lower constraint, an upper bound may not be the least upper bound, which is known as the supremum.
Differences Between Infimum and Upper Bound
The infimum of a set is the greatest element that is less than or equal to all elements of the set, often referred to as the greatest lower bound. In contrast, an upper bound is any element that is greater than or equal to every element in the set, but it may not be the smallest such element. Unlike upper bounds, the infimum must be the maximal value among all lower bounds, highlighting a key difference in their roles within order theory.
Properties of the Infimum
The infimum of a set is the greatest lower bound, ensuring it is less than or equal to every element in the set while being the largest value with this property. It exists for any non-empty subset bounded below in an ordered set, often used in real analysis to define limits and continuity. Unlike an upper bound, which might not be the least, the infimum is unique and can belong to the set or lie outside it as the closest lower boundary.
Properties of Upper Bounds
An upper bound of a set in an ordered field is any element greater than or equal to every element in the set, ensuring the set is bounded above. Crucial properties include that the set of upper bounds is closed under taking greater elements, meaning if an element is an upper bound, any larger element is also an upper bound. The least upper bound, or supremum, is unique if it exists and serves as the smallest element in the set of all upper bounds, tightly bounding the set from above.
Examples Demonstrating Infimum
The infimum, or greatest lower bound, of a set such as \( S = \{ \frac{1}{n} : n \in \mathbb{N} \} \) is 0, even though 0 is not an element of \( S \). In contrast, an upper bound example can be seen with the set \( T = \{ x \in \mathbb{R} : x < 5 \} \) where 5 serves as the least upper bound or supremum, despite not belonging to \( T \). These examples highlight that the infimum and supremum may not be members of the set but still define critical bounds essential for analysis in real numbers.
Examples Demonstrating Upper Bound
An upper bound of a set is any value greater than or equal to every element in the set, such as 10 being an upper bound for the set {1, 5, 7}. For example, in the set of real numbers less than 5, the number 5 itself serves as an upper bound, while any number greater than 5, like 6 or 10, also qualifies as an upper bound. In contrast, the infimum is the greatest lower bound, which in this case for the set {1, 5, 7} would be 1, distinguishing the concept of upper bounds from infima.
Relation Between Infimum, Supremum, and Upper Bound
Infimum (greatest lower bound) and supremum (least upper bound) are closely tied to upper bounds within ordered sets; every supremum is an upper bound, but not every upper bound qualifies as a supremum. The infimum represents the highest value below all elements of a subset, whereas the supremum is the smallest value above or equal to all elements, making the supremum the minimal upper bound. Understanding the interplay between infimum, supremum, and upper bounds is essential in real analysis, lattice theory, and optimization problems to define limits and bounds precisely.
Importance of Infimum and Upper Bound in Analysis
The infimum represents the greatest lower bound of a set, ensuring precise characterization of limits and convergence in real analysis. The upper bound restricts values from above, crucial for defining boundedness and compactness in metric spaces. Together, these concepts underpin rigorous proofs and facilitate the understanding of function behavior and optimization problems.
Common Misconceptions and Clarifications
The infimum of a set is often mistaken for the minimum, but it represents the greatest lower bound, which may not be an element of the set, unlike the minimum that must belong to the set. An upper bound is any value greater than or equal to every element in the set, while the supremum is the least of those upper bounds, potentially not included in the set itself. Clarifying these distinctions helps avoid confusion between bounds as elements and bounds as limit points in real analysis and optimization contexts.
Infimum Infographic
 libterm.com
libterm.com