A Turing Machine is a theoretical computing model that manipulates symbols on a strip of tape according to a set of rules to simulate the logic of computer algorithms. It serves as the foundation for understanding computation, decidability, and complexity in computer science. Explore this article to deepen your knowledge about the principles and significance of Turing Machines.
Table of Comparison
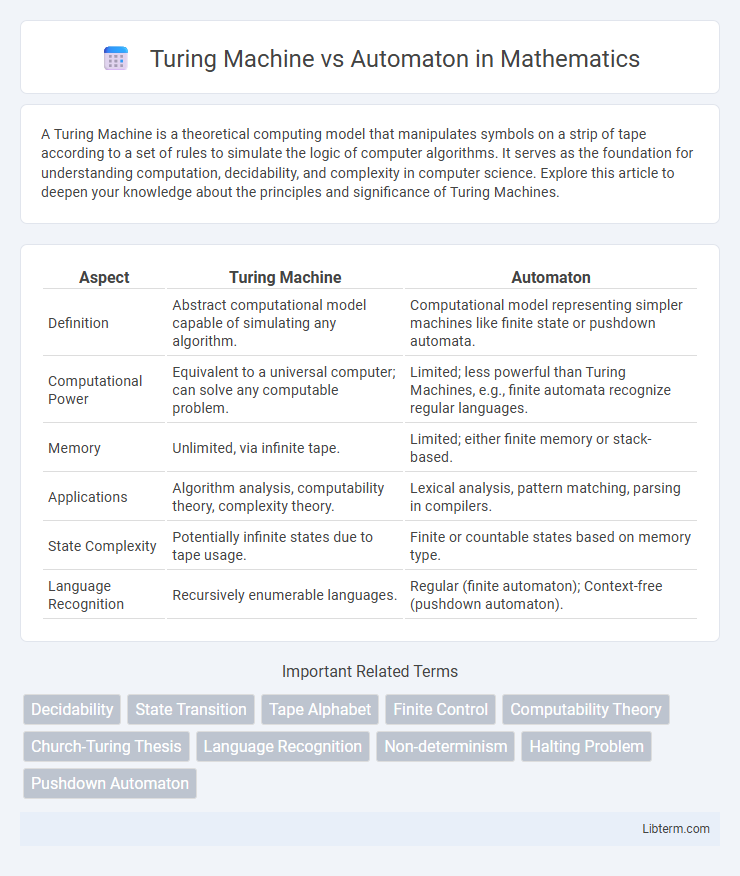
| Aspect | Turing Machine | Automaton |
|---|---|---|
| Definition | Abstract computational model capable of simulating any algorithm. | Computational model representing simpler machines like finite state or pushdown automata. |
| Computational Power | Equivalent to a universal computer; can solve any computable problem. | Limited; less powerful than Turing Machines, e.g., finite automata recognize regular languages. |
| Memory | Unlimited, via infinite tape. | Limited; either finite memory or stack-based. |
| Applications | Algorithm analysis, computability theory, complexity theory. | Lexical analysis, pattern matching, parsing in compilers. |
| State Complexity | Potentially infinite states due to tape usage. | Finite or countable states based on memory type. |
| Language Recognition | Recursively enumerable languages. | Regular (finite automaton); Context-free (pushdown automaton). |
Introduction to Turing Machines and Automata
Turing Machines and Automata serve as fundamental models in theoretical computer science for understanding computation and language recognition. A Turing Machine consists of an infinite tape, a tape head that reads and writes symbols, and states that dictate actions, enabling it to simulate any algorithmic process, thus representing the concept of algorithmic decidability. Automata, including finite automata and pushdown automata, are simpler machines used to recognize regular and context-free languages, respectively, emphasizing the hierarchy in computational power and language classes.
Historical Background of Computational Models
The historical background of computational models reveals that the Turing Machine, introduced by Alan Turing in 1936, formalized the concept of algorithmic computation and became foundational in computer science theory. Automata, conceptualized earlier through finite automata and pushdown automata, originated from efforts to understand language recognition and formal grammars in the 1950s and 1960s. Turing Machines extended these models by providing a more powerful abstract machine capable of simulating any algorithmic process, solidifying their role in defining computational limits.
Core Concepts: Turing Machine Explained
A Turing Machine is a theoretical computing model that manipulates symbols on an infinite tape according to a set of rules, providing a foundation for understanding algorithmic processes and computational limits. Unlike automata, which have finite states and memory, a Turing Machine features an infinite memory tape and a read-write head capable of moving bidirectionally, enabling it to solve a broader class of problems. The core concept centers on its ability to simulate any algorithm, establishing it as a universal model of computation in theoretical computer science.
Fundamental Principles of Automata
Automata operate based on finite state machines that transition between states according to input symbols, embodying the principles of determinism and nondeterminism. These models are characterized by their limited memory, using only the current state to determine behavior, which restricts them to recognizing regular languages. In contrast, Turing Machines possess an infinite tape serving as unbounded memory, enabling them to compute a broader class of languages, including recursively enumerable languages.
Types of Automata in Computation Theory
Types of automata in computation theory include finite automata, pushdown automata, and linear bounded automata, each varying in computational power and memory capacity. Finite automata recognize regular languages, pushdown automata handle context-free languages with a stack, and linear bounded automata operate within a bounded tape length to recognize context-sensitive languages. Turing machines surpass these automata by providing a model of computation with unlimited memory and the ability to simulate any algorithm.
Expressive Power: Turing Machine vs Automaton
Turing machines exhibit greater expressive power than automata, as they can simulate any algorithm and recognize recursively enumerable languages, while finite automata are limited to regular languages. Pushdown automata expand expressiveness by recognizing context-free languages, yet still fall short compared to Turing machines, which can handle context-sensitive and beyond. This difference stems from Turing machines' unlimited memory capacity and ability to perform arbitrary computations, unlike automata constrained by finite or stack-based memory.
Decidability and Computability Comparison
Turing machines provide a comprehensive framework for decidability and computability, capable of solving all problems that are algorithmically solvable, unlike automata which are limited to specific language classes such as regular or context-free languages. Decidability in Turing machines means a problem can be algorithmically decided with a yes or no answer in finite time, whereas automata are decidable only within their restricted language sets. Computability involves Turing machines being able to simulate any algorithm, while automata lack this power due to their structural limitations, highlighting the fundamental distinction in computational capabilities between the two models.
Real-World Applications of Turing Machines and Automata
Turing machines underpin modern computing by providing a theoretical framework for algorithm design, enabling advancements in software development, cryptography, and artificial intelligence. Automata theory is critical in designing lexical analyzers, parsers, and network protocols, as finite automata efficiently process regular languages and automate pattern recognition tasks. Both models drive innovations in compiler construction, natural language processing, and robotics, impacting real-world applications across diverse technological domains.
Limitations and Boundaries of Each Model
Turing machines exhibit superior computational power by simulating any algorithmic process, yet they operate under constraints such as infinite tape assumptions and undecidability problems like the halting problem. Automata, including finite automata and pushdown automata, have limited memory and computational abilities, restricting them to recognizing regular and context-free languages respectively, and cannot handle more complex language classes. These boundary distinctions highlight that automata are suitable for simpler pattern recognition tasks, whereas Turing machines underpin broader computational theory and universal problem-solving capabilities.
Conclusion: Choosing the Right Model for Computation
Turing machines offer universal computation capabilities, making them ideal for complex algorithmic problems and theoretical computer science tasks. Automata, such as finite automata and pushdown automata, provide efficient models for simpler language recognition tasks and are widely used in practical applications like lexical analysis and pattern matching. Selecting between a Turing machine and an automaton depends on the computational complexity, required memory, and specific problem constraints inherent to the task.
Turing Machine Infographic
 libterm.com
libterm.com