A normal operator in mathematics is a linear operator on a Hilbert space that commutes with its adjoint, meaning it satisfies the condition \(AA^* = A^*A\). These operators include important classes such as unitary, self-adjoint, and normal matrices, and they play a crucial role in spectral theory because they can be diagonalized by an orthonormal basis. Explore the rest of the article to deepen your understanding of normal operators and their applications in functional analysis.
Table of Comparison
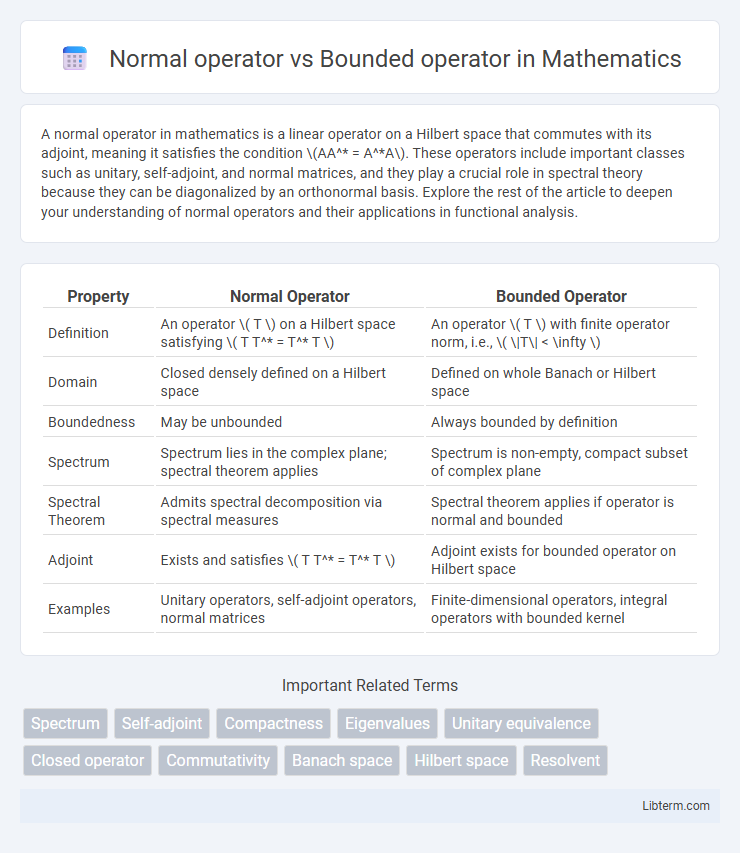
| Property | Normal Operator | Bounded Operator |
|---|---|---|
| Definition | An operator \( T \) on a Hilbert space satisfying \( T T^* = T^* T \) | An operator \( T \) with finite operator norm, i.e., \( \|T\| < \infty \) |
| Domain | Closed densely defined on a Hilbert space | Defined on whole Banach or Hilbert space |
| Boundedness | May be unbounded | Always bounded by definition |
| Spectrum | Spectrum lies in the complex plane; spectral theorem applies | Spectrum is non-empty, compact subset of complex plane |
| Spectral Theorem | Admits spectral decomposition via spectral measures | Spectral theorem applies if operator is normal and bounded |
| Adjoint | Exists and satisfies \( T T^* = T^* T \) | Adjoint exists for bounded operator on Hilbert space |
| Examples | Unitary operators, self-adjoint operators, normal matrices | Finite-dimensional operators, integral operators with bounded kernel |
Introduction to Operators in Functional Analysis
In functional analysis, a bounded operator is a linear operator between normed vector spaces that maps bounded sets to bounded sets, ensuring continuity and having a finite operator norm. A normal operator, defined on a Hilbert space, is a bounded operator that commutes with its adjoint, characterized by properties such as spectral theorem applicability and diagonalizability via unitary transformations. Understanding the distinction between bounded and normal operators is fundamental for studying operator spectra, functional calculus, and stability in infinite-dimensional spaces.
Defining Normal Operators
A normal operator on a Hilbert space is defined by the property that it commutes with its adjoint, meaning \( T T^* = T^* T \). This contrasts with bounded operators, which only require boundedness in norm but do not necessarily satisfy commutation relations. Normal operators encompass important classes such as unitary, self-adjoint, and normal matrices, enabling spectral theorem applications.
Understanding Bounded Operators
Bounded operators on a Hilbert space are linear operators with a finite operator norm, ensuring continuity and stability in function transformations. Normal operators are a special class of bounded operators that commute with their adjoints, meaning \( TT^* = T^*T \), enabling a spectral decomposition analogous to diagonalization. Understanding bounded operators is fundamental for studying operator theory, as their boundedness guarantees well-defined behavior under limits and enables powerful functional calculus tools.
Key Differences Between Normal and Bounded Operators
Normal operators on a Hilbert space satisfy the commutation relation \( AA^* = A^*A \), meaning they commute with their adjoints, while bounded operators are defined by having a finite operator norm \( \|A\| < \infty \). All normal operators are bounded, but not all bounded operators are normal, highlighting a key subset relationship. Normality implies diagonalizability via the spectral theorem, a property not guaranteed for general bounded operators.
Spectral Properties of Normal Operators
Normal operators on a Hilbert space satisfy the condition \( N^*N = NN^* \), ensuring they are diagonalizable by a unitary operator and have a spectral measure supported on their spectrum. Bounded operators, while continuous and defined on the whole space, do not necessarily exhibit commutativity with their adjoint, preventing a straightforward spectral decomposition. The spectral theorem for normal operators guarantees a spectral resolution via projection-valued measures, enabling functional calculus and precise analysis of their spectral properties, which is not generally applicable to arbitrary bounded operators.
Role of Boundedness in Operator Theory
Bounded operators play a crucial role in operator theory by ensuring continuity and stability within Hilbert spaces, which contrasts with normal operators where boundedness is a necessary condition for their spectral theorem application. The boundedness condition enables the use of functional calculus and facilitates the analysis of operator spectra, making bounded normal operators central to various mathematical and physical models. Unbounded operators, while important in quantum mechanics and differential operators, require more careful domain considerations, highlighting the foundational importance of boundedness in practical operator theory.
Examples of Normal and Bounded Operators
Normal operators on Hilbert spaces include unitary operators, such as the Fourier transform, and self-adjoint operators like Hermitian matrices, both exhibiting commutation with their adjoints. Bounded operators encompass all finite-dimensional linear transformations, such as matrices with finite norm, and integral operators with square-integrable kernels. Examples illustrate that while all normal operators are bounded, not all bounded operators satisfy the normality condition, highlighting differences in spectral properties and operational behavior.
Applications in Quantum Mechanics
Normal operators play a crucial role in quantum mechanics due to their spectral properties, enabling the diagonalization of observables like Hamiltonians, which represent energy measurements in a system. Bounded operators ensure the mathematical rigor and stability of quantum states by maintaining finite operator norms, essential for the well-defined evolution of quantum systems in Hilbert spaces. Applications involving normal and bounded operators facilitate the measurement postulates and unitary time evolution, underpinning core principles like superposition and eigenvalue spectra in quantum theory.
Importance in Hilbert and Banach Spaces
Normal operators on Hilbert spaces are crucial due to their spectral theorem, enabling diagonalization via orthonormal eigenbases, which simplifies functional calculus and quantum mechanics applications. Bounded operators, defined by norm constraints, ensure continuity and stability, essential for functional analysis in both Hilbert and Banach spaces, where unbounded operators pose domain and closure challenges. The distinction emphasizes the critical role of boundedness in operator theory, affecting spectral properties, norm topology, and the feasibility of extending operators in infinite-dimensional spaces.
Summary: Choosing the Right Operator
Normal operators maintain commutativity with their adjoints, ensuring spectral properties that facilitate diagonalization and stability in Hilbert spaces. Bounded operators guarantee continuity and a finite operator norm, essential for controlling behavior in functional analysis. Selecting between normal and bounded operators depends on the need for spectral decomposition versus operational continuity and norm constraints in the given mathematical context.
Normal operator Infographic
 libterm.com
libterm.com