Unlock the full potential of your digital marketing strategy with innovative techniques that drive engagement and boost conversions. By leveraging data-driven insights and tailoring content to your audience's preferences, you can significantly enhance your online presence. Explore the rest of this article to discover actionable tips that will transform your approach and deliver measurable results.
Table of Comparison
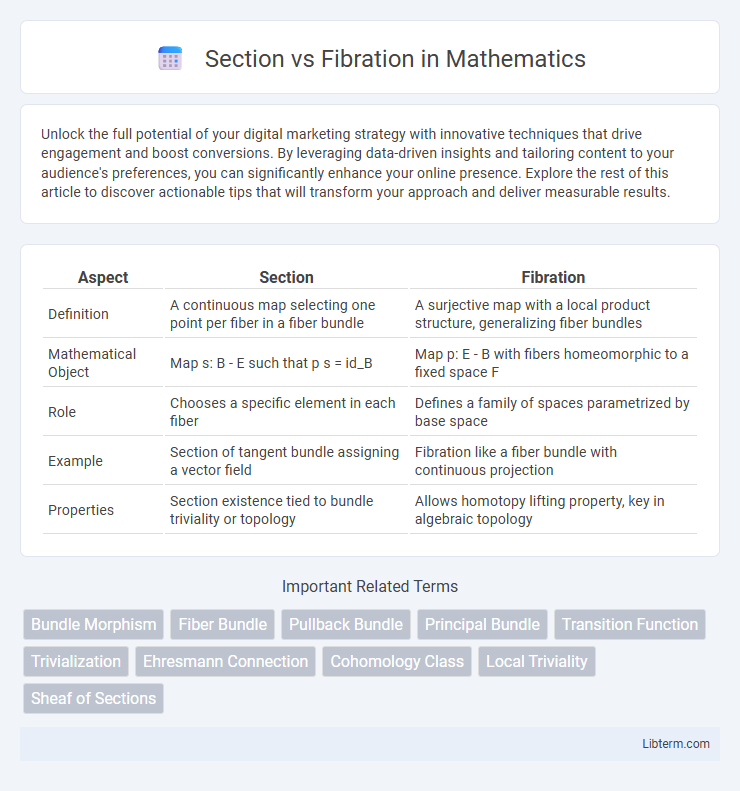
| Aspect | Section | Fibration |
|---|---|---|
| Definition | A continuous map selecting one point per fiber in a fiber bundle | A surjective map with a local product structure, generalizing fiber bundles |
| Mathematical Object | Map s: B - E such that p s = id_B | Map p: E - B with fibers homeomorphic to a fixed space F |
| Role | Chooses a specific element in each fiber | Defines a family of spaces parametrized by base space |
| Example | Section of tangent bundle assigning a vector field | Fibration like a fiber bundle with continuous projection |
| Properties | Section existence tied to bundle triviality or topology | Allows homotopy lifting property, key in algebraic topology |
Introduction to Sections and Fibrations
Sections and fibrations are fundamental concepts in topology and category theory, where a fibration is a special type of continuous map characterized by the homotopy lifting property, often used to study fiber bundles and their homotopy types. A section of a fibration is a continuous map that assigns to every point in the base space a point in the total space lying over it, effectively serving as a right inverse to the fibration map. Understanding sections helps in analyzing the structure of fibrations by providing a way to select canonical representatives in each fiber, which is crucial in obstruction theory and bundle classification.
Definitions: What is a Section?
A section is a continuous mapping from the base space of a fiber bundle to its total space, assigning each point in the base a point in the corresponding fiber. It serves as a right inverse to the bundle projection, ensuring the composition yields the identity on the base space. In contrast to fibrations, which emphasize the structural properties and homotopy lifting, sections provide explicit selections of fibers over each base point.
Understanding Fibrations: Key Concepts
Fibrations are continuous mappings between topological spaces that satisfy the homotopy lifting property, essential for studying fiber bundles and homotopy theory. A section is a continuous right inverse to a fibration, assigning each point in the base space a unique point in the fiber, thereby providing a global choice of elements within the fiber. Understanding fibrations involves analyzing the relationship between the base, total space, and fiber, with the section offering crucial insights into the structure and classification of these spaces.
Differences Between Sections and Fibrations
Sections are specific maps that select a single point in each fiber of a fibration, providing a continuous "choice" throughout the base space. Fibrations, however, refer to the overall structure consisting of a total space, base space, and fiber, along with a projection map satisfying the homotopy lifting property. The key difference lies in the role: sections pinpoint elements inside the fibers, while fibrations describe the entire fibered space topology and its projection.
The Role of Sections in Topology
Sections play a critical role in topology by providing continuous right inverses to fibrations, enabling the study of complex spaces via simpler base spaces and fibers. They allow the decomposition of a fibration into a product structure locally, facilitating the analysis of fiber bundles, classifying spaces, and homotopy lifting properties. The existence or obstruction of sections reveals essential topological invariants and can characterize fiber bundle triviality and cohomological features.
Importance of Fibrations in Mathematics
Fibrations play a crucial role in algebraic topology and category theory by providing a structured way to study spaces through continuous maps with homotopy lifting properties, enabling the analysis of complex topological objects via their fibers. Unlike sections, which are specific continuous selections of points from fibers, fibrations allow for a flexible and powerful framework to examine homotopy types and fiber bundles, making them essential in solving classification problems and understanding fiberwise phenomena. Their importance is underscored in applications ranging from homotopy theory and bundle theory to the study of spectral sequences and model categories.
Applications of Sections in Geometry
Sections serve as continuous selections of points in fiber bundles, enabling the construction of global properties and invariants in geometry. They facilitate the study of vector bundles, where smooth sections are used to define vector fields, connections, and characteristic classes. In differential geometry, sections help analyze curvature and topology by providing concrete realizations of abstract fiber structures.
Fibrations in Fiber Bundle Theory
Fibrations in fiber bundle theory represent continuous surjective maps that satisfy the homotopy lifting property, enabling the study of complex topological structures through their fibers. Unlike sections, which are right inverses selecting a specific point in each fiber, fibrations emphasize the global structure and relationships between the total space, base space, and fiber. Key examples include Serre fibrations and Hurewicz fibrations, which play crucial roles in algebraic topology and the classification of fiber bundles.
Examples Illustrating Sections and Fibrations
Sections in topology often arise from the projection map of a fiber bundle, such as the Hopf fibration \( S^3 \to S^2 \) where a section corresponds to a continuous selection of points from each fiber \( S^1 \). A classical example of a section is the Mobius strip as a bundle over \( S^1 \) with fiber \( \mathbb{R} \), where no continuous non-vanishing section exists due to its nontrivial twisting. Fibrations, exemplified by the projection from a torus \( T^2 \) onto a circle \( S^1 \), demonstrate how fibers (copies of \( S^1 \)) vary continuously, although sections may or may not exist depending on the bundle's structure.
Implications in Modern Mathematical Research
Sections of fiber bundles allow for the selection of continuous choices across fibers, facilitating explicit constructions in topology and gauge theory. Fibrations, characterized by the homotopy lifting property, provide a framework for analyzing complex spaces through long exact sequences and spectral sequences, crucial in algebraic topology and homotopy theory. The interplay between sections and fibrations underpins advances in modern mathematical research, influencing areas such as bundle theory, category theory, and the study of moduli spaces.
Section Infographic
 libterm.com
libterm.com