Hermitian matrices are fundamental in linear algebra and quantum mechanics due to their unique property of having real eigenvalues and orthogonal eigenvectors. These matrices play a crucial role in various applications such as signal processing, vibration analysis, and stability calculations in engineering. Explore the full article to understand how Hermitian matrices can enhance your mathematical and physical problem-solving skills.
Table of Comparison
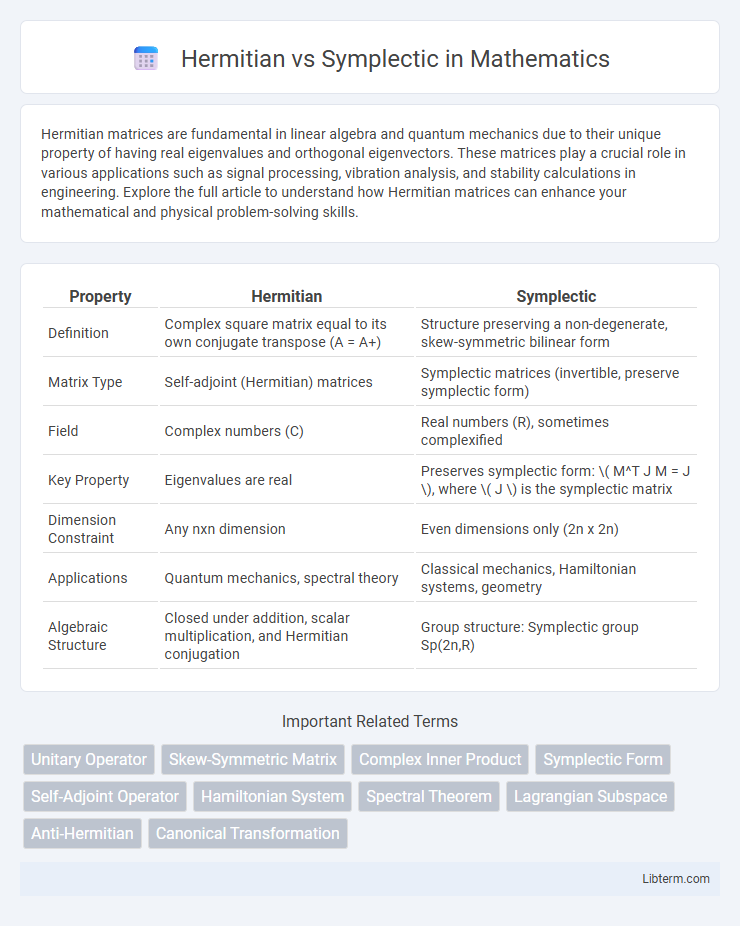
| Property | Hermitian | Symplectic |
|---|---|---|
| Definition | Complex square matrix equal to its own conjugate transpose (A = A+) | Structure preserving a non-degenerate, skew-symmetric bilinear form |
| Matrix Type | Self-adjoint (Hermitian) matrices | Symplectic matrices (invertible, preserve symplectic form) |
| Field | Complex numbers (C) | Real numbers (R), sometimes complexified |
| Key Property | Eigenvalues are real | Preserves symplectic form: \( M^T J M = J \), where \( J \) is the symplectic matrix |
| Dimension Constraint | Any nxn dimension | Even dimensions only (2n x 2n) |
| Applications | Quantum mechanics, spectral theory | Classical mechanics, Hamiltonian systems, geometry |
| Algebraic Structure | Closed under addition, scalar multiplication, and Hermitian conjugation | Group structure: Symplectic group Sp(2n,R) |
Introduction to Hermitian and Symplectic Structures
Hermitian structures define complex vector spaces with an inner product that is linear in one argument and conjugate linear in the other, ensuring a positive-definite, sesquilinear form invariant under unitary transformations. Symplectic structures involve nondegenerate, skew-symmetric bilinear forms on even-dimensional real vector spaces, essential in classical and quantum mechanics for preserving phase space geometry. Both structures play crucial roles in differential geometry and mathematical physics, with Hermitian structures underpinning complex geometry and symplectic structures governing symplectic manifolds.
Mathematical Foundations of Hermitian Spaces
Hermitian spaces are complex vector spaces equipped with a Hermitian form, a sesquilinear form that is conjugate symmetric and positive-definite, forming the foundation for complex inner product spaces and enabling the study of complex eigenvalues and unitary transformations. In contrast, symplectic spaces involve a non-degenerate, skew-symmetric bilinear form essential for the geometry of phase spaces in classical and quantum mechanics. The mathematical foundations of Hermitian spaces provide crucial structures for quantum theory, spectral analysis, and complex manifold theory, whereas symplectic geometry underpins Hamiltonian dynamics and classical mechanics.
Core Principles of Symplectic Geometry
Symplectic geometry centers on the study of symplectic manifolds equipped with a closed, non-degenerate 2-form known as the symplectic form, which fundamentally differs from the Hermitian structure that includes a compatible complex structure and positive-definite metric. The core principle of symplectic geometry involves the preservation of the symplectic form under diffeomorphisms, leading to Hamiltonian dynamics and canonical transformations in phase space. Unlike Hermitian geometry, which mainly pertains to complex vector spaces with inner products, symplectic geometry lacks a notion of length or angle but emphasizes volume preservation and the interplay between position and momentum coordinates.
Key Differences Between Hermitian and Symplectic Forms
Hermitian forms are complex-valued sesquilinear forms that are conjugate symmetric and positive definite, making them fundamental in complex inner product spaces and quantum mechanics. Symplectic forms are skew-symmetric, non-degenerate bilinear forms essential in symplectic geometry and classical mechanics, particularly in the study of Hamiltonian systems. The key difference lies in Hermitian forms being associated with metric structures inducing lengths and angles, while symplectic forms provide a geometric framework for phase space and preserve area rather than distance.
Applications in Quantum Mechanics and Physics
Hermitian operators represent observables in quantum mechanics, ensuring real eigenvalues and orthogonal eigenstates critical for measurement outcomes and system stability. Symplectic transformations preserve the canonical commutation relations in phase space, underpinning classical and quantum Hamiltonian dynamics, including the evolution of wavefunctions and quantum states. Applications of Hermitian matrices dominate quantum spectroscopy and state measurement, while symplectic matrices are essential in quantum optics, quantum information theory, and the study of entanglement.
Algebraic Properties: Comparing Hermitian and Symplectic Matrices
Hermitian matrices are complex square matrices that are equal to their own conjugate transpose, characterized by real eigenvalues and orthonormal eigenvectors, which guarantee diagonalizability over the complex field. Symplectic matrices, defined over even-dimensional spaces, preserve a non-degenerate, skew-symmetric bilinear form and form a subgroup of the general linear group with determinant one, highlighting their structure in symplectic geometry and Hamiltonian mechanics. Unlike Hermitian matrices, symplectic matrices are generally not diagonalizable but can be decomposed using the symplectic spectral theorem, emphasizing distinct algebraic properties regarding eigenvalue distribution and matrix invariance.
Role in Complex and Real Vector Spaces
Hermitian matrices play a crucial role in complex vector spaces by defining inner products that ensure conjugate symmetry and positive definiteness, which are fundamental for quantum mechanics and signal processing. Symplectic matrices, on the other hand, arise in real vector spaces as linear transformations preserving the symplectic form, essential in classical mechanics and Hamiltonian systems for maintaining geometric structure. The distinction centers on Hermitian forms inducing complex inner products, while symplectic forms preserve skew-symmetric bilinear forms in even-dimensional real spaces.
Invariant Transformations in Hermitian vs Symplectic Contexts
Invariant transformations in Hermitian contexts preserve the Hermitian form, ensuring unitary symmetry characterized by complex conjugate transpose operations. In contrast, symplectic invariant transformations maintain the symplectic form, a non-degenerate skew-symmetric bilinear form, underpinning phase space geometry in classical and quantum mechanics. These differences highlight the distinct mathematical structures where Hermitian invariance relates to inner product preservation, while symplectic invariance governs canonical transformations preserving the symplectic structure.
Examples and Case Studies in Mathematics
Hermitian matrices, exemplified by the complex conjugate transpose equality in quantum mechanics operators, ensure real eigenvalues and orthogonal eigenvectors, fundamental in spectral theory. Symplectic matrices, central in classical mechanics and Hamiltonian systems, preserve the symplectic form and are illustrated by canonical transformations in phase space, maintaining area and structure in dynamical systems. Case studies comparing Hermitian vs symplectic behavior highlight their roles in stability analysis and conservation laws across mathematical physics applications.
Conclusion: Choosing Between Hermitian and Symplectic Approaches
Choosing between Hermitian and Symplectic approaches depends on the specific mathematical or physical context; Hermitian frameworks excel in quantum mechanics for ensuring real eigenvalues and preserving inner products, while Symplectic methods are essential in classical mechanics for maintaining the structure of phase space and Hamiltonian dynamics. Hermitian operators guarantee self-adjointness crucial for observable quantities in quantum systems, whereas symplectic matrices preserve the symplectic form, critical for the evolution of canonical coordinates. The decision hinges on whether the problem requires the spectral properties and stability of Hermitian structures or the geometric and dynamical invariants upheld by symplectic geometry.
Hermitian Infographic
 libterm.com
libterm.com