Covectors play a crucial role in differential geometry and physics, representing linear functionals that map vectors to scalars, essential for understanding dual spaces. They are fundamental in formulating concepts like gradients and differential forms, aiding in the description of physical phenomena such as electromagnetism and general relativity. Discover how mastering covectors can deepen your grasp of advanced mathematical structures and their applications throughout this article.
Table of Comparison
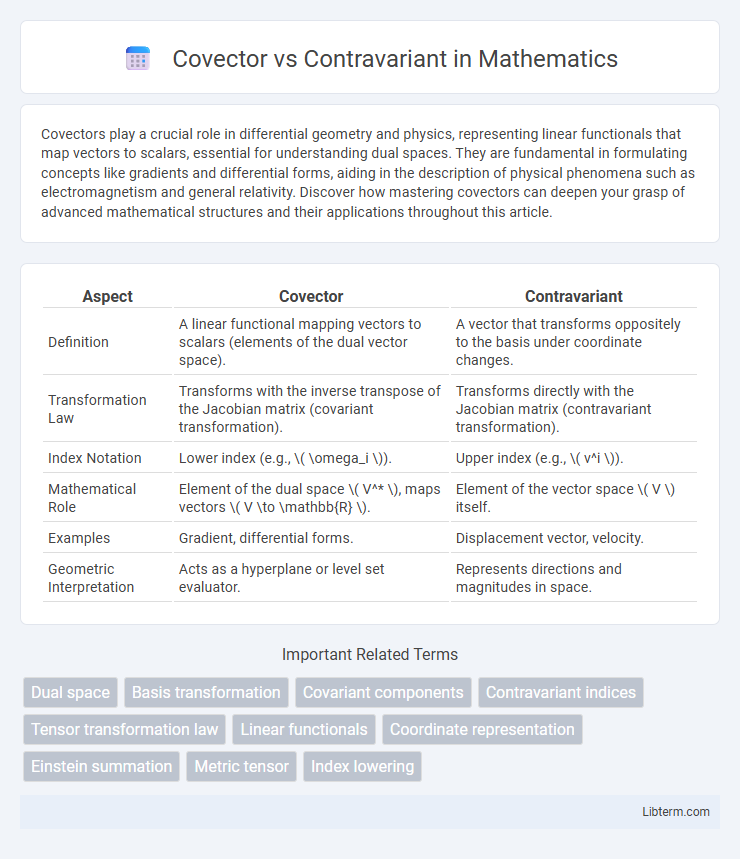
| Aspect | Covector | Contravariant |
|---|---|---|
| Definition | A linear functional mapping vectors to scalars (elements of the dual vector space). | A vector that transforms oppositely to the basis under coordinate changes. |
| Transformation Law | Transforms with the inverse transpose of the Jacobian matrix (covariant transformation). | Transforms directly with the Jacobian matrix (contravariant transformation). |
| Index Notation | Lower index (e.g., \( \omega_i \)). | Upper index (e.g., \( v^i \)). |
| Mathematical Role | Element of the dual space \( V^* \), maps vectors \( V \to \mathbb{R} \). | Element of the vector space \( V \) itself. |
| Examples | Gradient, differential forms. | Displacement vector, velocity. |
| Geometric Interpretation | Acts as a hyperplane or level set evaluator. | Represents directions and magnitudes in space. |
Understanding Covectors and Contravariant Vectors
Covectors, also known as dual vectors, are linear functionals that map vectors to scalars, forming the dual space of a vector space. Contravariant vectors transform according to the inverse of the coordinate change matrix, preserving their geometric nature under coordinate transformations. Understanding the relationship between covectors and contravariant vectors is fundamental in differential geometry and tensor analysis, where covectors act as linear maps on contravariant vectors.
Covector vs Contravariant: Core Definitions
A covector, also known as a dual vector, is a linear functional that maps vectors from a vector space to scalars, residing in the dual space of that vector space. Contravariant vectors transform oppositely to the coordinate basis under a change of coordinates, reflecting how vector components adjust inversely to the basis vectors. Covectors (covariant entities) and contravariant vectors differ fundamentally in their transformation properties, with covectors transforming covariantly and vectors transforming contravariantly.
Mathematical Representation: Covectors and Contravariant Vectors
Covectors are linear functionals on vector spaces, represented mathematically as elements of the dual space \( V^* \), mapping vectors in \( V \) to scalars. Contravariant vectors correspond to elements of the original vector space \( V \) and transform under coordinate changes by the inverse of the Jacobian matrix. The interaction is captured by the pairing \( \langle \omega, v \rangle = \omega(v) \) where \( \omega \in V^* \) is a covector and \( v \in V \) is a contravariant vector.
Transformation Properties: Covariant and Contravariant Behavior
Covariant transformations preserve the direction of morphisms between categories, allowing objects and arrows to map consistently in the same direction, facilitating functors like hom-functors that respect the structure. Contravariant transformations reverse the direction of morphisms, such as in the case of dual vector spaces or contravariant functors, where the transformation flips arrows while maintaining structural integrity. Understanding covariant versus contravariant behavior is critical in category theory, algebra, and functional programming for correctly modeling how functions or data types transform under mappings.
Basis Vectors: Dual vs Standard
Covector basis vectors form the dual space of a vector space, mapping standard basis vectors to scalars via linear functionals, while standard basis vectors represent elements within the original vector space. Each covector basis vector corresponds to a unique functional that extracts the coefficient of a specific standard basis vector in a vector's linear combination. This duality provides a fundamental framework for transforming and interpreting vectors and covectors within linear algebra and tensor analysis.
Index Notation: Contravariant (Upper) and Covariant (Lower)
Contravariant vectors have upper indices, such as \( V^i \), representing components that transform with the inverse Jacobian matrix under coordinate changes, reflecting their role in mapping basis covectors. Covariant vectors, or covectors, possess lower indices, like \( \omega_i \), and transform with the Jacobian matrix itself, tracking how differentials change with coordinates. This index notation distinction is crucial in tensor calculus because it ensures correct transformation properties and maintains the geometric meaning across coordinate systems.
Geometric Interpretation of Covectors and Contravariant Vectors
Covectors can be interpreted geometrically as hyperplanes or level sets that assign scalar values to vectors, representing linear functionals on a vector space, while contravariant vectors correspond to directional quantities that transform oppositely under coordinate changes. In differential geometry, contravariant vectors are tangent vectors that represent directions on a manifold, whereas covectors (or covariant vectors) act as gradients or differential forms that measure rates of change along these directions. The duality between covectors and contravariant vectors is fundamental in defining metrics and transformations that map vectors to scalars through inner products and pullbacks.
Physical Examples and Applications
Covectors represent linear functionals that map vectors to scalars, such as gradient fields in physics where they assign a directional derivative to displacement vectors, exemplified by the gradient of temperature or pressure in a fluid. Contravariant vectors correspond to physical quantities like velocity or displacement that transform inversely to coordinate changes, maintaining direction and magnitude under spatial transformations. In differential geometry and general relativity, contravariant vectors describe tangent vectors on manifolds, while covectors denote differential forms, essential for expressing physical laws invariant under coordinate transformations.
Covector and Contravariant in Differential Geometry
Covectors in differential geometry are linear functionals that map tangent vectors at a point on a manifold to real numbers, forming the dual space of the tangent space. Contravariant vectors transform according to the inverse Jacobian matrix under coordinate changes, reflecting their nature as elements of the tangent space itself. Covariant objects like covectors transform with the Jacobian matrix, highlighting the duality and distinction between contravariant vectors and covariant covectors in tensor calculus.
Key Differences: Covector vs Contravariant Summary
Covectors, also known as linear functionals, map vectors to scalars and belong to the dual space of a vector space, characterized by their transformation with the inverse transpose of the original vector transformation. Contravariant vectors, in contrast, transform directly with the change of basis matrix, maintaining their vector nature under coordinate transformations. The key difference lies in their transformation rules: covectors transform covariantly (with the inverse coordinate transformation), while contravariant vectors transform contravariantly (with the coordinate transformation itself), reflecting their roles in differential geometry and tensor analysis.
Covector Infographic
 libterm.com
libterm.com