Ergodic theory explores the statistical behavior of dynamical systems over time, ensuring that time averages equal space averages under certain conditions. This mathematical framework has critical applications in physics, probability, and information theory. Discover how ergodic principles can deepen your understanding of complex systems in the rest of this article.
Table of Comparison
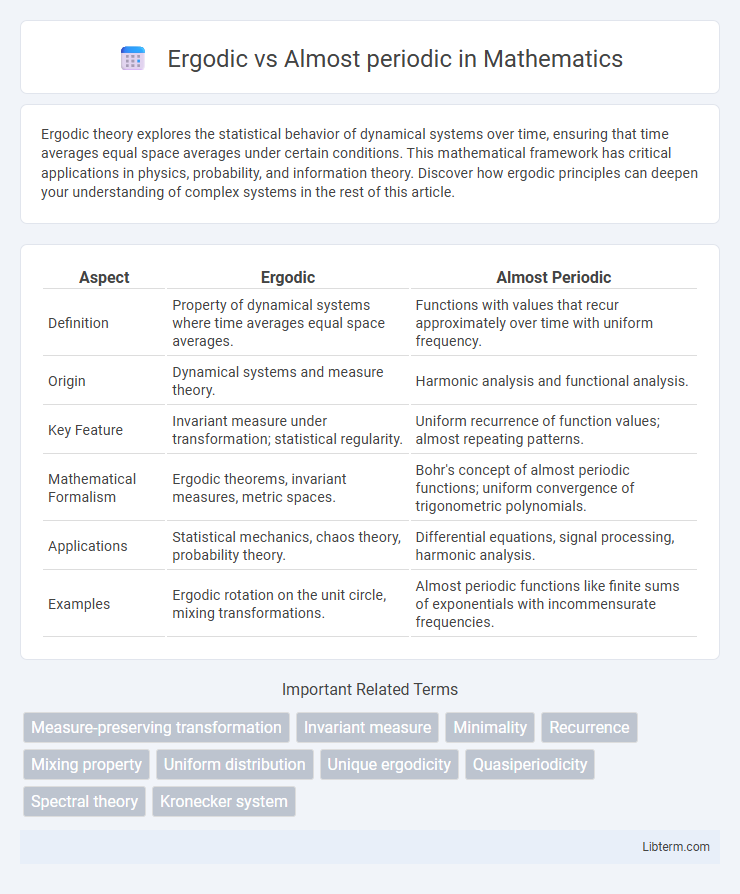
| Aspect | Ergodic | Almost Periodic |
|---|---|---|
| Definition | Property of dynamical systems where time averages equal space averages. | Functions with values that recur approximately over time with uniform frequency. |
| Origin | Dynamical systems and measure theory. | Harmonic analysis and functional analysis. |
| Key Feature | Invariant measure under transformation; statistical regularity. | Uniform recurrence of function values; almost repeating patterns. |
| Mathematical Formalism | Ergodic theorems, invariant measures, metric spaces. | Bohr's concept of almost periodic functions; uniform convergence of trigonometric polynomials. |
| Applications | Statistical mechanics, chaos theory, probability theory. | Differential equations, signal processing, harmonic analysis. |
| Examples | Ergodic rotation on the unit circle, mixing transformations. | Almost periodic functions like finite sums of exponentials with incommensurate frequencies. |
Introduction to Ergodic and Almost Periodic Systems
Ergodic systems exhibit statistical properties that remain invariant under time evolution, ensuring time averages equal space averages for almost all initial points. Almost periodic systems possess functions that recur over time with arbitrary precision but do not require statistical uniformity across the entire space. Understanding the distinction between ergodic and almost periodic systems is fundamental in dynamical systems theory, particularly in studying long-term behavior and stability of solutions.
Defining Ergodicity in Dynamical Systems
Ergodicity in dynamical systems describes a property where time averages of observables converge to space averages for almost all initial points, ensuring statistical uniformity over the system's phase space. Unlike almost periodic systems, which exhibit recurrent behavior with functions returning arbitrarily close to initial states, ergodic systems explore the entirety of the phase space in a measure-theoretic sense. This fundamental distinction allows ergodic theory to analyze long-term average behavior, crucial for understanding chaotic systems and statistical mechanics.
Almost Periodicity: Concepts and Examples
Almost periodic functions generalize periodic functions by allowing for irregular intervals while maintaining recurring patterns throughout their domain. These functions exhibit uniform recurrence, making them essential in modeling phenomena in physics and engineering where signals or states repeat over time without fixed periods. Classic examples include trigonometric polynomials with incommensurate frequencies and the Bohr almost periodic functions, which satisfy uniform approximation by finite linear combinations of exponentials.
Mathematical Foundations: Key Differences
Ergodic theory focuses on the statistical behavior of dynamical systems over time, ensuring that time averages converge to space averages for almost all initial points, whereas almost periodic functions generalize periodic functions by allowing uniform approximations through finite sums of exponential functions with frequencies forming relatively dense sets. The key mathematical difference lies in ergodic systems emphasizing measure-preserving transformations and invariant measures on metric spaces, while almost periodicity involves uniform convergence and the compactness of the set of translates in function spaces. Ergodicity pertains to long-term statistical uniformity in dynamical systems, but almost periodicity captures recurring structural regularity without strict periodicity constraints.
Ergodic Theorem vs Almost Periodic Functions
The Ergodic Theorem establishes that, for a measure-preserving dynamical system, time averages converge to space averages almost everywhere, providing a foundational result in statistical mechanics and dynamical systems theory. Almost periodic functions, characterized by their uniform recurrence and relatively dense sets of e-almost periods, differ fundamentally as their behavior mimics periodicity without strict periodicity, enabling uniform approximation by trigonometric polynomials. While the Ergodic Theorem emphasizes long-term average behavior in stochastic or chaotic contexts, almost periodic functions highlight deterministic, recurrent structures with strong uniform continuity properties.
Physical and Mathematical Applications
Ergodic theory analyzes the long-term average behavior of dynamical systems, crucial in statistical mechanics for predicting equilibrium states in physical systems. Almost periodic functions, characterized by recurrent patterns, find applications in signal processing and quantum mechanics to model systems with near-repetitive behavior over time. Mathematically, ergodic theorems provide foundation for measure-preserving transformations, while almost periodicity extends Fourier analysis to non-periodic but recurrent phenomena.
Indicators of Ergodic Behavior
Ergodic behavior is indicated by time averages converging to ensemble averages, reflecting statistical uniformity over time in dynamical systems. In contrast, almost periodic functions exhibit recurrence without necessarily satisfying the mixing properties essential for ergodicity. Key indicators of ergodic behavior include invariant measures, metric transitivity, and the Birkhoff Ergodic Theorem, which guarantees convergence of time averages for integrable functions.
Recognizing Almost Periodic Patterns
Almost periodic patterns are characterized by functions that repeat their values within any given tolerance over relatively dense sets of time, enabling recognition of near-repetitive behaviors in signals or dynamical systems. Unlike ergodic processes, which exhibit statistical regularity over time, almost periodic functions ensure uniform recurrence of patterns without requiring long-term averaging. Identifying almost periodic patterns involves analyzing frequency components through tools like Bohr or Besicovitch almost periodicity, facilitating detection of stable, recurring structures within complex datasets.
Advantages and Limitations of Each Concept
Ergodic theory excels in analyzing the long-term average behavior of dynamical systems, ensuring that time averages converge to space averages, which is advantageous in statistical mechanics and probability. Almost periodic functions provide a strong form of recurrence with uniform approximation by trigonometric polynomials, beneficial for solving differential equations with non-constant coefficients. However, ergodic systems may lack uniformity and can be sensitive to initial conditions, limiting predictability, while almost periodicity requires stricter regularity conditions, restricting applicability to more general or chaotic systems.
Conclusion: Choosing Ergodic or Almost Periodic Frameworks
Choosing between ergodic and almost periodic frameworks depends on the nature of the underlying system and desired statistical properties. Ergodic frameworks excel in systems where time averages converge to ensemble averages, enabling long-term statistical predictions in stochastic or chaotic processes. Almost periodic frameworks suit systems exhibiting recurring patterns over time, providing robust tools for analyzing deterministic signals with inherent regularity and quasi-periodicity.
Ergodic Infographic
 libterm.com
libterm.com