Divisible numbers can be evenly divided by another number without leaving a remainder, making them fundamental in mathematics and everyday calculations. Understanding divisibility rules simplifies problem-solving and helps identify factors quickly. Explore the rest of this article to master the concept of divisibility and enhance your numerical skills.
Table of Comparison
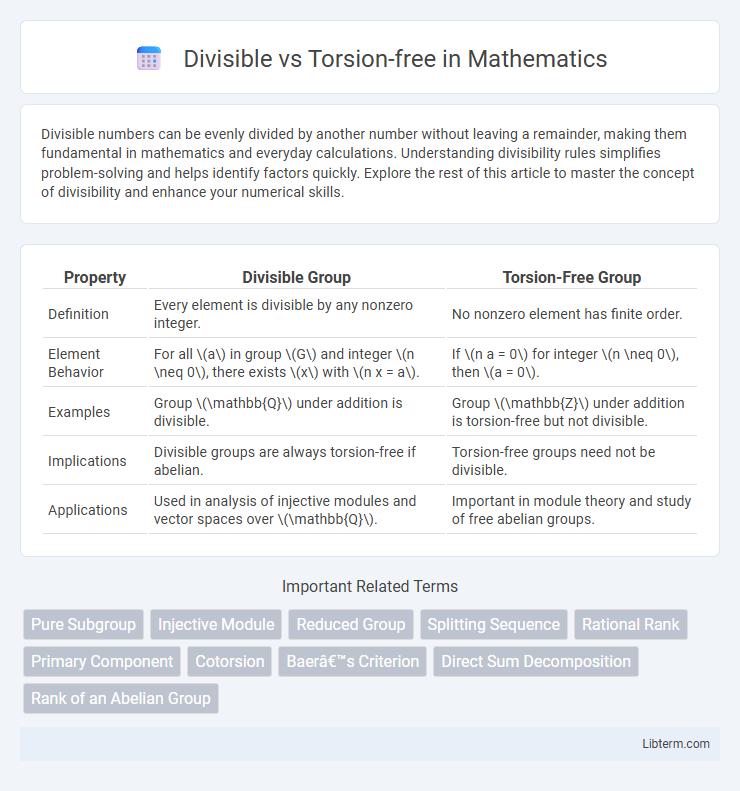
| Property | Divisible Group | Torsion-Free Group |
|---|---|---|
| Definition | Every element is divisible by any nonzero integer. | No nonzero element has finite order. |
| Element Behavior | For all \(a\) in group \(G\) and integer \(n \neq 0\), there exists \(x\) with \(n x = a\). | If \(n a = 0\) for integer \(n \neq 0\), then \(a = 0\). |
| Examples | Group \(\mathbb{Q}\) under addition is divisible. | Group \(\mathbb{Z}\) under addition is torsion-free but not divisible. |
| Implications | Divisible groups are always torsion-free if abelian. | Torsion-free groups need not be divisible. |
| Applications | Used in analysis of injective modules and vector spaces over \(\mathbb{Q}\). | Important in module theory and study of free abelian groups. |
Introduction to Divisible and Torsion-Free Groups
Divisible groups are abelian groups where every element can be expressed as an n-th multiple of another element for any positive integer n, ensuring an inherent "divisibility" structure. Torsion-free groups are abelian groups that contain no non-zero elements of finite order, meaning every non-zero element has infinite order. Understanding these foundational properties highlights the distinction between groups with divisible elements and those entirely free from torsion elements, central to the study of module theory and abelian group classification.
Defining Divisible Groups
Divisible groups are abelian groups in which every element can be expressed as a multiple of another element for any nonzero integer, meaning for each element \( g \) and integer \( n \), there exists an element \( h \) such that \( nh = g \). This property distinguishes divisible groups from torsion-free groups, where no nonzero element has finite order, ensuring the absence of elements annihilated by any nonzero integer. Divisible groups serve as crucial examples in the classification of abelian groups, often containing both torsion and torsion-free components.
Understanding Torsion-Free Groups
Torsion-free groups are algebraic structures where no element other than the identity has finite order, meaning for any non-identity element \(g\), \(g^n \neq e\) for all \(n > 0\). In contrast, divisible groups allow every element to be expressed as an \(n\)-th power of another element, ensuring solutions to equations like \(x^n = g\) exist for all integers \(n\). Understanding torsion-free groups is crucial in areas such as group theory and module theory, where their lack of finite order elements influences the structure and classification of groups and modules over integral domains.
Key Differences Between Divisible and Torsion-Free
Divisible groups are algebraic structures where every element can be expressed as a multiple of another element for any integer, while torsion-free groups have no nonzero elements of finite order, meaning they contain no elements that become zero when multiplied by a nonzero integer. The key difference lies in the presence of elements divisible by any integer in divisible groups, contrasted with the absence of torsion elements in torsion-free groups, making torsion-free groups a subset that excludes elements with finite order. Divisible groups are often used in module theory and are examples of injective abelian groups, whereas torsion-free groups frequently appear in the study of free abelian groups and integral domains.
Algebraic Properties and Implications
Divisible groups are algebraic structures where every element is expressible as a multiple of another element, ensuring solvability of equations like nx = a for all n in the integers, which implies these groups lack elements of finite order except the identity. Torsion-free groups exclude elements with finite order, meaning no non-identity element satisfies nx = 0 for any nonzero integer n, reflecting a structural rigidity that separates them from divisible groups possibly containing torsion elements. Understanding the distinction between divisible and torsion-free groups is crucial in module theory and homological algebra, where divisible groups often act as injective objects and torsion-free groups serve as building blocks for free modules over integral domains.
Examples of Divisible Groups
Divisible groups include classic examples such as the additive group of rational numbers \(\mathbb{Q}\) and the vector space \(\mathbb{R}^n\) over the real numbers, where every element can be expressed as a multiple of another element for any integer. These groups contrast with torsion-free groups like \(\mathbb{Z}\), which contain no elements of finite order except the identity but lack the divisibility property. The group \(\mathbb{Q}/\mathbb{Z}\) is a canonical example of a divisible group with torsion elements, illustrating that divisibility does not imply torsion-freeness.
Examples of Torsion-Free Groups
Torsion-free groups include examples such as the additive group of integers \(\mathbb{Z}\), free abelian groups, and the fundamental group of a torus, all of which contain no elements of finite order other than the identity. Divisible groups, like the additive group of rational numbers \(\mathbb{Q}\), differ by allowing elements to be infinitely divisible, while torsion-free groups prohibit nontrivial torsion elements. In algebraic topology and group theory, torsion-free groups play a crucial role in classifying spaces and modules without finite cyclic substructures.
Relationship Between Divisibility and Torsion-Freeness
Divisible groups are always torsion-free because every element can be divided by any positive integer, ensuring no nontrivial elements have finite order. However, torsion-free groups are not necessarily divisible, as they may lack elements that are multiples of others for all integers. The relationship highlights that divisibility implies torsion-freeness, but torsion-free groups allow a broader class of structures without the divisibility condition.
Applications in Modern Algebra
Divisible groups play a crucial role in module theory and homological algebra, where their injective properties facilitate the classification of abelian groups and the construction of injective resolutions. Torsion-free groups are fundamental in the study of integral domains and vector spaces over fields, providing a framework for analyzing modules without torsion elements and enabling the extension of scalar multiplication. Applications in modern algebra leverage the interplay between divisible and torsion-free structures to address problems in algebraic number theory, representation theory, and cohomology.
Summary and Comparison Table
Divisible groups are abelian groups in which every element is divisible by any positive integer, meaning for each element \(x\) and integer \(n > 0\), there exists \(y\) such that \(ny = x\). Torsion-free groups contain no nontrivial elements of finite order; for any \(x \neq 0\) in the group and integer \(n > 0\), \(nx = 0\) implies \(x = 0\). The comparison table highlights that divisible groups allow for solving equations \(ny = x\) within the group, while torsion-free groups strictly lack elements annihilated by nonzero integers, with divisible groups often being torsion-free but not all torsion-free groups are divisible.
Divisible Infographic
 libterm.com
libterm.com