The De Rham complex is a fundamental construct in differential geometry that links differential forms with topology, enabling the study of manifold properties through algebraic methods. This complex reveals deep insights into the structure of smooth manifolds by connecting exterior derivatives and cohomology groups. Explore the full article to understand how the De Rham complex can enhance your grasp of topological invariants and manifold theory.
Table of Comparison
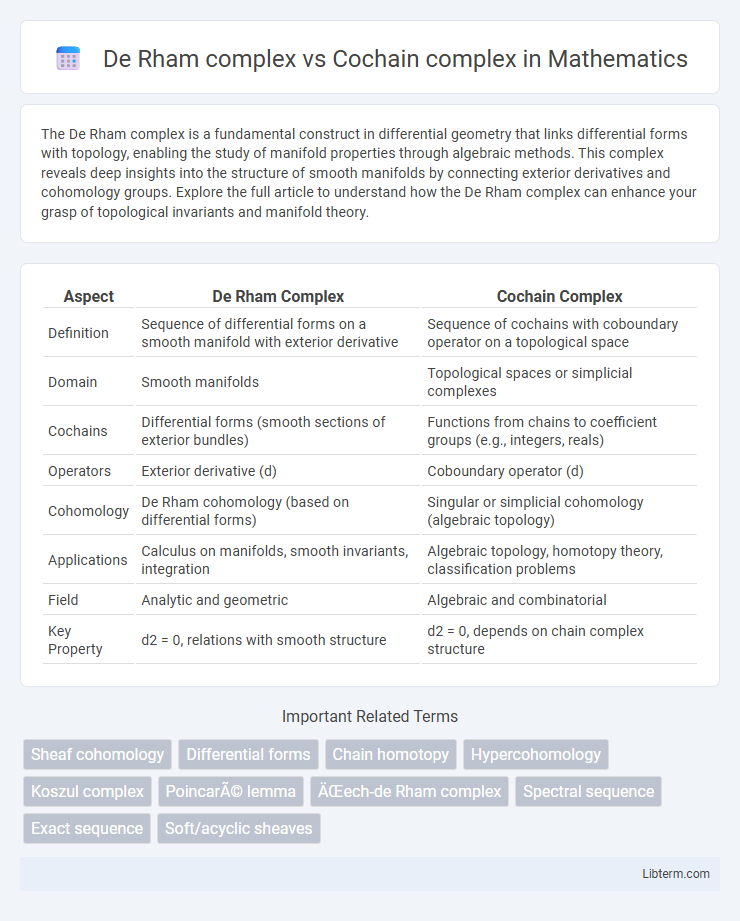
| Aspect | De Rham Complex | Cochain Complex |
|---|---|---|
| Definition | Sequence of differential forms on a smooth manifold with exterior derivative | Sequence of cochains with coboundary operator on a topological space |
| Domain | Smooth manifolds | Topological spaces or simplicial complexes |
| Cochains | Differential forms (smooth sections of exterior bundles) | Functions from chains to coefficient groups (e.g., integers, reals) |
| Operators | Exterior derivative (d) | Coboundary operator (d) |
| Cohomology | De Rham cohomology (based on differential forms) | Singular or simplicial cohomology (algebraic topology) |
| Applications | Calculus on manifolds, smooth invariants, integration | Algebraic topology, homotopy theory, classification problems |
| Field | Analytic and geometric | Algebraic and combinatorial |
| Key Property | d2 = 0, relations with smooth structure | d2 = 0, depends on chain complex structure |
Introduction to De Rham and Cochain Complexes
The De Rham complex is a fundamental tool in differential geometry, consisting of smooth differential forms on a manifold with the exterior derivative as its differential operator, capturing topological information via De Rham cohomology. In contrast, cochain complexes arise in algebraic topology as sequences of abelian groups or modules connected by coboundary maps, providing an algebraic framework for computing cohomology groups of topological spaces. Both complexes serve to study geometric and topological invariants, with the De Rham complex linking differential calculus to topology, while cochain complexes abstract these concepts into purely algebraic settings.
Foundations: Differential Forms vs. Abstract Chains
The De Rham complex is founded on differential forms, which are smooth antisymmetric tensor fields enabling integration over manifolds and capturing geometric properties via exterior derivatives. In contrast, the cochain complex is an abstract algebraic construction composed of cochains--functions on chains or simplices--that generalize topological spaces without requiring smooth structure. While the De Rham complex leverages calculus on manifolds for topological invariants, cochain complexes provide a purely algebraic framework useful in homological algebra and topological data analysis.
Construction of the De Rham Complex
The De Rham complex is constructed by taking the sequence of differential forms on a smooth manifold with the exterior derivative acting as the boundary operator, forming a cochain complex. Each space in the complex consists of smooth differential k-forms, and the exterior derivative maps k-forms to (k+1)-forms, satisfying d2=0 to ensure complex structure. This setup contrasts with the general cochain complex, which may not be defined by differential forms but rather by abstract group or module homomorphisms between chain groups.
Understanding the Cochain Complex
The cochain complex is a sequence of abelian groups or modules connected by homomorphisms whose compositions are zero, central to algebraic topology for computing cohomology groups. Unlike the De Rham complex, which uses differential forms on smooth manifolds, the cochain complex deals more abstractly with functions on simplicial or cellular decompositions, enabling applications beyond smooth contexts. Understanding the cochain complex involves grasping its algebraic structure, the role of coboundary operators, and how cohomology classes arise as equivalence classes of cocycles modulo coboundaries.
Key Differences in Structure and Interpretation
The De Rham complex consists of differential forms on a smooth manifold with exterior derivatives connecting them, emphasizing geometric and analytic properties, while the Cochain complex is an abstract algebraic construction involving abelian groups or modules connected by coboundary maps. In the De Rham complex, the focus is on smooth structures, integration, and differential geometry, whereas the Cochain complex underpins algebraic topology, encoding topological invariants via cohomology with various coefficients. Structurally, the De Rham complex uses differential forms graded by degree, and its cohomology corresponds to de Rham cohomology, isomorphic to singular cohomology with real coefficients reflected by the Cochain complex framework.
Cohomology: De Rham vs. Singular Cohomology
De Rham cohomology computes topological invariants of smooth manifolds using differential forms and the exterior derivative, yielding isomorphic results to singular cohomology with real coefficients in smooth settings. Singular cohomology arises from cochain complexes defined on singular simplices, providing a purely topological invariant applicable to a broader class of spaces. The De Rham theorem establishes the isomorphism between De Rham cohomology groups and singular cohomology groups with real coefficients, bridging differential geometry and algebraic topology.
Role in Algebraic Topology and Geometry
The De Rham complex plays a crucial role in differential geometry by linking differential forms to the topology of smooth manifolds through De Rham cohomology, enabling the computation of topological invariants via integration of closed forms. The cochain complex, central to algebraic topology, systematically encodes topological spaces using algebraic objects like groups or modules, facilitating the calculation of cohomology groups that classify topological features such as holes and connectivity. Together, these complexes provide complementary frameworks: the De Rham complex offers a geometric and analytic perspective, while the cochain complex provides an abstract, combinatorial approach to understanding spaces.
Applications and Computations
The De Rham complex, based on differential forms, is extensively used in smooth manifold analysis for computing topological invariants like de Rham cohomology, which directly relates to the manifold's geometry and differential structure. The Cochain complex, constructed from algebraic or combinatorial inputs such as simplicial complexes, excels in computational topology and homological algebra by enabling algorithmic calculation of cohomology groups via discrete data. Applications of the De Rham complex often involve continuous settings like differential geometry and physics, while Cochain complexes are fundamental in computer science, robotics, and data analysis for efficient discrete computations of topological features.
The Importance of the de Rham Theorem
The de Rham theorem establishes a fundamental isomorphism between de Rham cohomology groups, defined via differential forms in the de Rham complex, and singular cohomology groups, constructed from the cochain complex of topological spaces. This isomorphism bridges smooth differential geometry and algebraic topology, allowing topological invariants to be studied using analytical tools like differential forms. By providing a direct link between these two complexes, the theorem plays a crucial role in understanding the topology of manifolds through calculus-based methods.
Comparative Summary and Future Perspectives
The De Rham complex, rooted in differential forms on smooth manifolds, offers a geometric framework for analyzing topological properties through integration and exterior differentiation, while the Cochain complex, often defined in algebraic topology via group cohomology or simplicial sets, provides an algebraic approach to computing invariants like cohomology groups. Comparative analysis highlights that De Rham cohomology is computationally effective for smooth manifolds and directly connects to differential geometry, whereas cochain complexes exhibit greater flexibility in discrete and abstract settings, including simplicial and cellular complexes. Future research aims to bridge these frameworks through generalized cohomology theories and enhanced computational algorithms, leveraging advances in homotopical algebra and categorical methods to unify differential and algebraic approaches in topological data analysis and mathematical physics.
De Rham complex Infographic
 libterm.com
libterm.com