A metric is a quantifiable measure used to evaluate performance, progress, or quality in various fields such as business, technology, or science. It helps in making informed decisions by providing clear and objective data points. Explore the full article to understand how selecting the right metrics can enhance your analysis and outcomes.
Table of Comparison
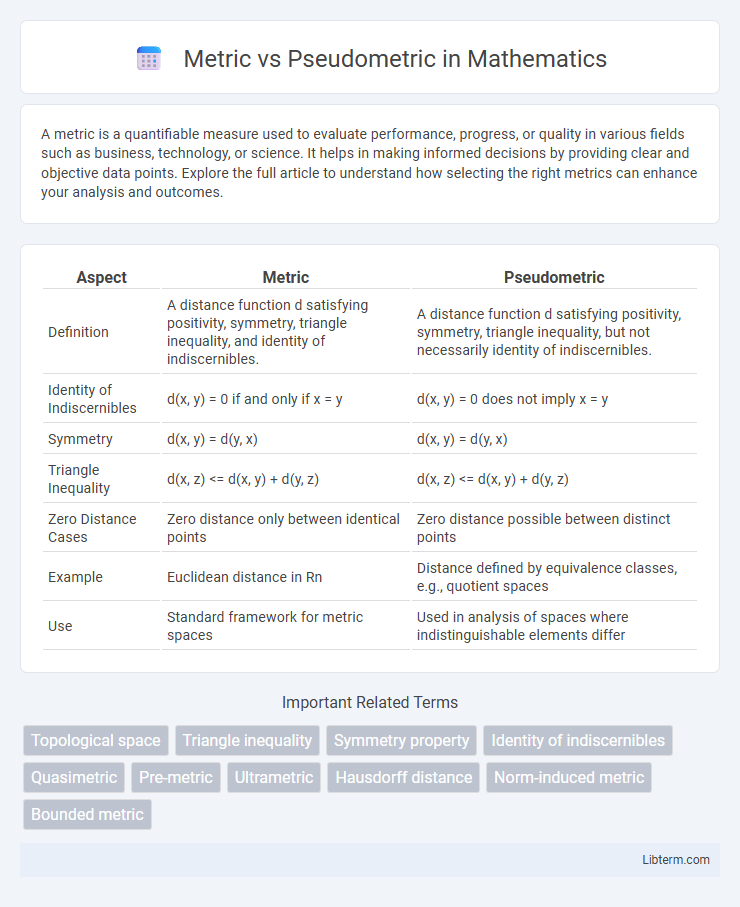
| Aspect | Metric | Pseudometric |
|---|---|---|
| Definition | A distance function d satisfying positivity, symmetry, triangle inequality, and identity of indiscernibles. | A distance function d satisfying positivity, symmetry, triangle inequality, but not necessarily identity of indiscernibles. |
| Identity of Indiscernibles | d(x, y) = 0 if and only if x = y | d(x, y) = 0 does not imply x = y |
| Symmetry | d(x, y) = d(y, x) | d(x, y) = d(y, x) |
| Triangle Inequality | d(x, z) <= d(x, y) + d(y, z) | d(x, z) <= d(x, y) + d(y, z) |
| Zero Distance Cases | Zero distance only between identical points | Zero distance possible between distinct points |
| Example | Euclidean distance in Rn | Distance defined by equivalence classes, e.g., quotient spaces |
| Use | Standard framework for metric spaces | Used in analysis of spaces where indistinguishable elements differ |
Introduction to Metric and Pseudometric Spaces
Metric spaces are defined by a distance function satisfying positivity, symmetry, and the triangle inequality, ensuring a clear measure of distance between points. Pseudometric spaces relax the positivity condition, allowing distinct points to have zero distance, which broadens applications in functional analysis and topology. These foundational concepts enable rigorous analysis of spatial properties, convergence, and continuity within diversified mathematical frameworks.
Definitions: Metric vs Pseudometric
A metric is a distance function d on a set X satisfying non-negativity, identity of indiscernibles, symmetry, and the triangle inequality, meaning d(x,y) = 0 if and only if x = y. A pseudometric relaxes this by allowing d(x,y) = 0 for distinct points x y, while still fulfilling non-negativity, symmetry, and the triangle inequality. This distinction makes metrics suitable for distinguishing points uniquely, whereas pseudometrics permit identifying different points at zero distance.
Key Properties of Metrics
Metrics satisfy key properties including non-negativity, identity of indiscernibles, symmetry, and the triangle inequality, ensuring a robust and intuitive measure of distance. Pseudometrics relax the identity condition, allowing distinct points to have zero distance, which can be useful in clustering and equivalence relations. This distinction impacts the topology induced by the distance function and the type of space analyzed in mathematical and applied contexts.
Characteristics of Pseudometrics
Pseudometrics differ from metrics by allowing distinct points to have zero distance, relaxing the identity of indiscernibles property. This means a pseudometric space permits non-unique identification of elements since d(x, y) = 0 does not necessarily imply x = y. The other properties--non-negativity, symmetry, and the triangle inequality--are preserved, making pseudometrics useful in contexts like function spaces and quotient topology where equivalence classes are essential.
Main Differences Between Metric and Pseudometric
The main differences between metric and pseudometric spaces lie in their distance properties: a metric requires that the distance between two distinct points is always positive, while a pseudometric allows the distance to be zero for distinct points. Metrics satisfy the identity of indiscernibles, meaning d(x, y) = 0 if and only if x = y, whereas pseudometrics relax this condition. Both satisfy non-negativity, symmetry, and the triangle inequality, but the pseudometric's allowance for zero distance between different points leads to less strict equivalence classes.
Common Examples in Mathematics
Metrics are functions defining distances satisfying positivity, symmetry, and the triangle inequality, with common examples including the Euclidean distance in \(\mathbb{R}^n\) and the discrete metric assigning 1 for distinct points. Pseudometrics relax the definiteness condition, allowing distinct points to have zero distance, as seen in the quotient space construction where points are identified under an equivalence relation. Typical examples include the semimetric derived from a norm on a vector space modulo a subspace and the Hausdorff pseudometric used in measure theory and fractal geometry.
Applications of Metric Spaces
Metric spaces, characterized by distances that satisfy non-negativity, identity of indiscernibles, symmetry, and the triangle inequality, are fundamental in fields such as topology, computer science, and machine learning for analyzing convergence, continuity, and clustering. Pseudometric spaces relax the identity condition, allowing distinct points to have zero distance, which proves useful in functional analysis and data science for studying equivalence classes and similarity relations. Applications of metric spaces include defining geometric structures in physics, enabling similarity measures in image recognition, and facilitating algorithm efficiency in nearest neighbor searches.
Uses of Pseudometric Spaces
Pseudometric spaces find significant applications in functional analysis, where they help analyze convergence and continuity in spaces that do not require distinct points to have positive distance. They are instrumental in studying quotient spaces and identifying equivalent points under an equivalence relation, enabling the construction of metric spaces from pseudometric ones. Pseudometrics also appear in computer science for measuring similarity in data clustering and pattern recognition, where exact distances are less critical than relational structures.
Transitioning from Pseudometric to Metric
Transitioning from a pseudometric to a metric involves ensuring the separation axiom, where the distance between distinct points is strictly positive rather than zero. This transition requires refining the pseudometric space by identifying and collapsing points with zero distance into single equivalence classes, effectively creating a metric space. The resulting metric preserves symmetry, non-negativity, and the triangle inequality, defining a true metric topology essential for precise distance measurement.
Summary and Key Takeaways
A metric is a distance function on a set that satisfies non-negativity, identity of indiscernibles, symmetry, and the triangle inequality, ensuring precise measurement of distance between points. A pseudometric relaxes the identity of indiscernibles condition, allowing distinct points to have zero distance, which is useful in quotient spaces and similarity measures. Key takeaways highlight that metrics provide strict separation of points, while pseudometrics enable grouping and are essential in applications like clustering and topology.
Metric Infographic
 libterm.com
libterm.com