A bijective continuous map ensures a one-to-one correspondence between elements of two topological spaces while preserving continuity in both directions. This concept plays a crucial role in topology by establishing homeomorphisms that indicate when two spaces are topologically equivalent. Discover how understanding bijective continuous maps can deepen your grasp of topological structure by reading the full article.
Table of Comparison
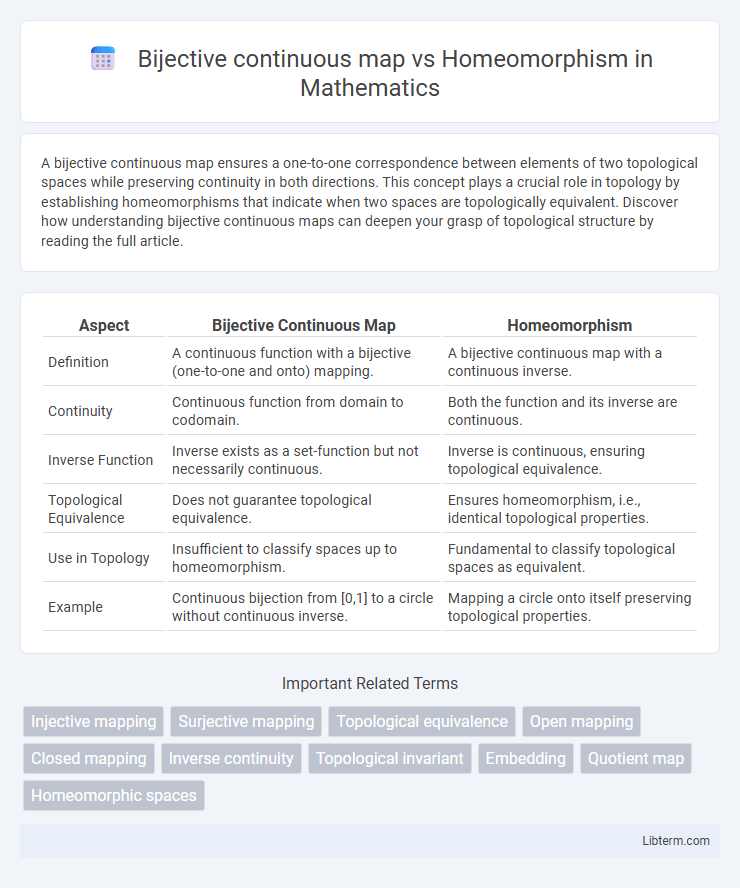
| Aspect | Bijective Continuous Map | Homeomorphism |
|---|---|---|
| Definition | A continuous function with a bijective (one-to-one and onto) mapping. | A bijective continuous map with a continuous inverse. |
| Continuity | Continuous function from domain to codomain. | Both the function and its inverse are continuous. |
| Inverse Function | Inverse exists as a set-function but not necessarily continuous. | Inverse is continuous, ensuring topological equivalence. |
| Topological Equivalence | Does not guarantee topological equivalence. | Ensures homeomorphism, i.e., identical topological properties. |
| Use in Topology | Insufficient to classify spaces up to homeomorphism. | Fundamental to classify topological spaces as equivalent. |
| Example | Continuous bijection from [0,1] to a circle without continuous inverse. | Mapping a circle onto itself preserving topological properties. |
Introduction to Bijective Continuous Maps
A bijective continuous map is a function between topological spaces that is both continuous and one-to-one onto its image, ensuring a perfect pairing between elements of the spaces. Unlike homeomorphisms, which require the inverse function to also be continuous, bijective continuous maps do not guarantee topological equivalence unless this inverse continuity holds. Understanding bijective continuous maps lays the groundwork for exploring homeomorphisms, critical for classifying spaces up to topological isomorphism.
Defining Homeomorphisms in Topology
A homeomorphism is a bijective continuous map between topological spaces with a continuous inverse, establishing a topological equivalence. While a bijective continuous map ensures a one-to-one and onto correspondence with continuity, it lacks the guarantee of the inverse map being continuous, which is essential for a homeomorphism. Defining homeomorphisms is fundamental in topology as they classify spaces up to topological equivalence, preserving properties like connectedness and compactness.
Key Properties of Bijective Continuous Maps
Bijective continuous maps are functions between topological spaces that are both one-to-one and onto, preserving the structure by ensuring each point in the target space corresponds uniquely to a point in the domain. Key properties include continuity combined with bijectiveness, but unlike homeomorphisms, their inverses may not be continuous, which means the map might not preserve topological equivalence. Homeomorphisms require both the map and its inverse to be continuous, establishing a strong form of topological isomorphism.
Criteria for Homeomorphism
A bijective continuous map between topological spaces is not necessarily a homeomorphism unless its inverse is also continuous. The essential criterion for a homeomorphism requires that both the map and its inverse preserve topological properties, ensuring a topological equivalence. This means a homeomorphism induces a one-to-one correspondence with continuous mappings in both directions, maintaining open sets and topological structure intact.
Bijectivity and Continuity: Are They Enough?
Bijective continuous maps establish a one-to-one correspondence between topological spaces, but they do not guarantee a homeomorphism without ensuring the continuity of the inverse map. Homeomorphisms require both the map and its inverse to be continuous, preserving topological properties and structure. Therefore, bijectivity and continuity alone are insufficient to confirm that two spaces are topologically equivalent.
Counterexamples: Bijective Continuous vs Homeomorphism
A bijective continuous map between topological spaces is not necessarily a homeomorphism if its inverse is not continuous. Classic counterexamples include the identity map from the real line with the usual topology to the real line with the lower limit topology, which is bijective and continuous but not a homeomorphism. Such examples highlight the crucial role of inverse continuity in ensuring a bijective continuous map qualifies as a homeomorphism.
Role of Inverse Continuity
A bijective continuous map guarantees a one-to-one correspondence between two topological spaces but does not ensure the inverse map is continuous. Homeomorphisms require both the map and its inverse to be continuous, establishing a topological equivalence. The continuity of the inverse function is crucial for preserving topological properties and confirming a true homeomorphic relationship.
Practical Implications in Topological Spaces
A bijective continuous map ensures a one-to-one and onto correspondence between two topological spaces but does not guarantee the inverse is continuous, limiting its ability to preserve topological properties. A homeomorphism, characterized by a bijective continuous map with a continuous inverse, establishes a strong equivalence between spaces, allowing for interchangeable application of topological invariants and tools. In practical terms, identifying homeomorphisms enables classification of spaces up to topological equivalence, critical for analyzing continuity, compactness, and connectedness properties in fields like geometric modeling and functional analysis.
Common Misconceptions and Pitfalls
A bijective continuous map between topological spaces is not necessarily a homeomorphism because the inverse function must also be continuous to preserve topological structure. A common misconception is assuming bijectivity and continuity alone guarantee a homeomorphism, neglecting that the inverse map's continuity is essential. Pitfalls arise when spaces differ in properties like compactness or connectedness, causing the inverse map to fail continuity despite the original map being bijective and continuous.
Summary: Distinguishing Homeomorphisms from Bijective Continuous Maps
A bijective continuous map is a function between topological spaces that is one-to-one, onto, and continuous, but it does not necessarily preserve topological properties such as open sets in both directions. A homeomorphism is a bijective continuous map whose inverse is also continuous, establishing a topological equivalence between spaces and preserving properties like connectedness and compactness. The key distinction lies in the continuity of the inverse map, which guarantees that the two spaces share the same topological structure, making homeomorphisms the isomorphisms in topology.
Bijective continuous map Infographic
 libterm.com
libterm.com