Semisimple structures are foundational in algebra, particularly in the study of modules and Lie algebras, characterized by their decomposition into simple components without any nontrivial radical. These structures enable clearer understanding and classification of algebraic objects due to their well-behaved behavior under morphisms and extensions. Explore the rest of this article to deepen your grasp of semisimple concepts and their applications.
Table of Comparison
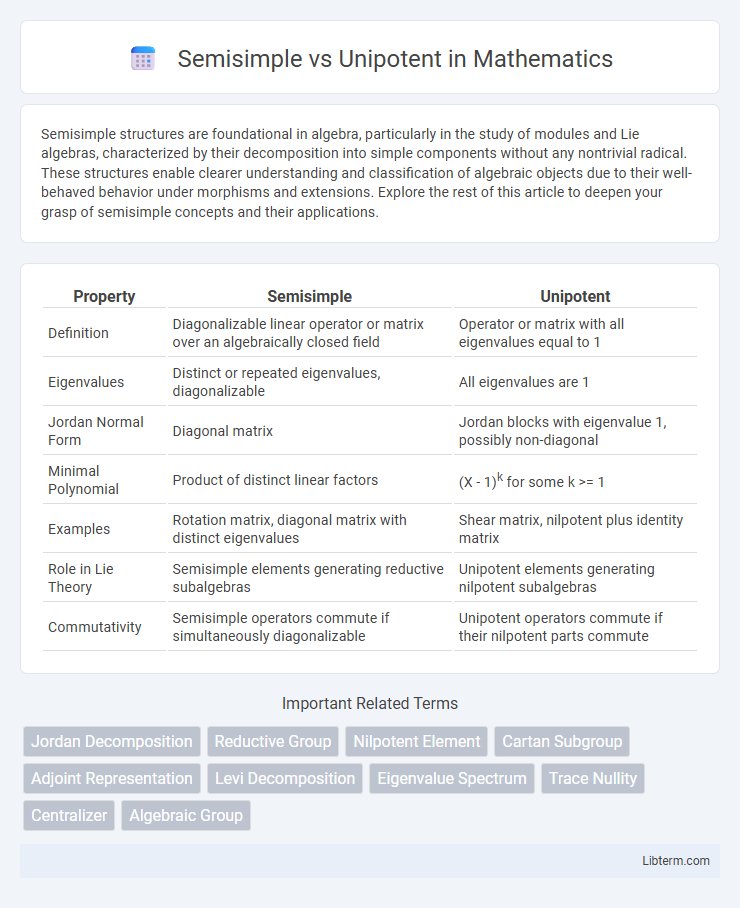
| Property | Semisimple | Unipotent |
|---|---|---|
| Definition | Diagonalizable linear operator or matrix over an algebraically closed field | Operator or matrix with all eigenvalues equal to 1 |
| Eigenvalues | Distinct or repeated eigenvalues, diagonalizable | All eigenvalues are 1 |
| Jordan Normal Form | Diagonal matrix | Jordan blocks with eigenvalue 1, possibly non-diagonal |
| Minimal Polynomial | Product of distinct linear factors | (X - 1)k for some k >= 1 |
| Examples | Rotation matrix, diagonal matrix with distinct eigenvalues | Shear matrix, nilpotent plus identity matrix |
| Role in Lie Theory | Semisimple elements generating reductive subalgebras | Unipotent elements generating nilpotent subalgebras |
| Commutativity | Semisimple operators commute if simultaneously diagonalizable | Unipotent operators commute if their nilpotent parts commute |
Introduction to Semisimple and Unipotent Elements
Semisimple elements in linear algebraic groups are those whose action can be diagonalized over an algebraic closure, characterized by eigenvalues without nilpotent parts. Unipotent elements, in contrast, have all eigenvalues equal to one and exhibit nilpotent behavior in their Jordan decomposition. Understanding these elements is fundamental in the structure theory of algebraic groups, as every element can be uniquely expressed as the product of a semisimple and a unipotent element commuting with each other.
Definitions: What Are Semisimple and Unipotent Elements?
Semisimple elements are those diagonalizable over an algebraically closed field, characterized by having a complete set of eigenvectors and eigenvalues lying in the field. Unipotent elements are those whose eigenvalues are all equal to one and can be represented as the identity matrix plus a nilpotent matrix. These definitions play a crucial role in the structure theory of linear algebraic groups and Lie algebras.
Key Differences Between Semisimple and Unipotent Elements
Semisimple elements in linear algebraic groups are diagonalizable over an algebraic closure, characterized by having distinct eigenvalues and a decomposition into eigenspaces. Unipotent elements have all eigenvalues equal to one and can be represented as upper triangular matrices with ones on the diagonal, exhibiting nilpotent behavior in their Jordan normal form. The key difference lies in their spectral properties: semisimple elements emphasize eigenvalue multiplicity and diagonalizability, while unipotent elements reflect nilpotent transformations with a single eigenvalue equal to one.
Semisimple Elements in Linear Algebraic Groups
Semisimple elements in linear algebraic groups are those that can be diagonalized over an algebraic closure, exhibiting a spectrum of eigenvalues with distinct eigenspaces, reflecting their stable and decomposable nature. These elements contrast with unipotent elements, which have all eigenvalues equal to one and are characterized by nilpotent Jordan blocks. The classification of semisimple elements forms the foundation for understanding the structure and representation theory of algebraic groups, enabling decompositions into simpler components and facilitating the study of group actions on vector spaces.
Properties of Unipotent Elements
Unipotent elements in algebraic groups are characterized by having all eigenvalues equal to one, which implies that their Jordan normal form consists solely of ones on the diagonal and possibly nonzero entries just above the diagonal. These elements are always of infinite order in characteristic zero fields but can be of finite order in positive characteristic. Unipotent elements form a normal, connected, and nilpotent subgroup called the unipotent radical, playing a critical role in the structure and classification of linear algebraic groups.
Jordan Decomposition: Connecting Semisimple and Unipotent
The Jordan decomposition uniquely expresses a linear operator as the product of its semisimple and unipotent components, where the semisimple part is diagonalizable and the unipotent part has all eigenvalues equal to one. This decomposition reveals the intrinsic structure of a linear transformation by separating its behavior into purely scaling (semisimple) and nilpotent-like (unipotent) actions. Understanding how these components interact provides a deeper insight into representation theory, algebraic groups, and Lie algebras by clarifying the role of eigenvalues and Jordan blocks.
Examples of Semisimple vs Unipotent Elements
Semisimple elements in linear algebraic groups are diagonalizable over an algebraic closure, such as the matrix \(\begin{pmatrix} 3 & 0 \\ 0 & 5 \end{pmatrix}\) in \(GL_2(\mathbb{C})\), while unipotent elements have all eigenvalues equal to 1, exemplified by \(\begin{pmatrix} 1 & 1 \\ 0 & 1 \end{pmatrix}\). Semisimple elements correspond to semisimple operators with distinct eigenvalues, and unipotent elements correspond to nilpotent conjugacy classes combined with the identity matrix. The Jordan decomposition uniquely expresses any element as a product of a semisimple and a unipotent element that commute with each other.
Applications in Representation Theory
Semisimple and unipotent elements play crucial roles in representation theory, particularly in the classification of linear algebraic groups and their modules. Semisimple elements, characterized by diagonalizable actions, facilitate decompositions of representations into simple components, aiding the study of irreducible modules and weight space analysis. Unipotent elements, with their nilpotent Jordan blocks, are essential in understanding the structure of nilpotent orbits, Springer correspondence, and the behavior of representations over fields of positive characteristic.
Importance in Algebraic Geometry and Group Theory
Semisimple and unipotent elements play crucial roles in algebraic geometry and group theory by influencing the structure and classification of algebraic groups and varieties. Semisimple elements correspond to diagonalizable actions, enabling decomposition into simpler, invariant subspaces essential for understanding group representations and geometric symmetries. Unipotent elements, characterized by nilpotent behavior, govern the complexity of group actions and degeneration in algebraic varieties, impacting the study of algebraic group schemes and moduli spaces.
Conclusion: Choosing Between Semisimple and Unipotent
Choosing between semisimple and unipotent elements depends on the algebraic structure and desired properties; semisimple elements facilitate diagonalization and simplify representations, while unipotent elements capture nilpotent behavior crucial for understanding Jordan decomposition. In linear algebraic groups and Lie algebras, clear separation of semisimple and unipotent parts enables precise structural analysis and classification. Selecting the appropriate focus enhances computational efficiency and theoretical insight in representation theory and algebraic geometry.
Semisimple Infographic
 libterm.com
libterm.com