Theta functions play a crucial role in various branches of mathematics, including number theory, complex analysis, and mathematical physics. These special functions exhibit periodicity and transformation properties that make them essential in studying elliptic functions, modular forms, and heat distribution. Explore the rest of this article to uncover how theta functions can deepen your understanding of these complex mathematical concepts.
Table of Comparison
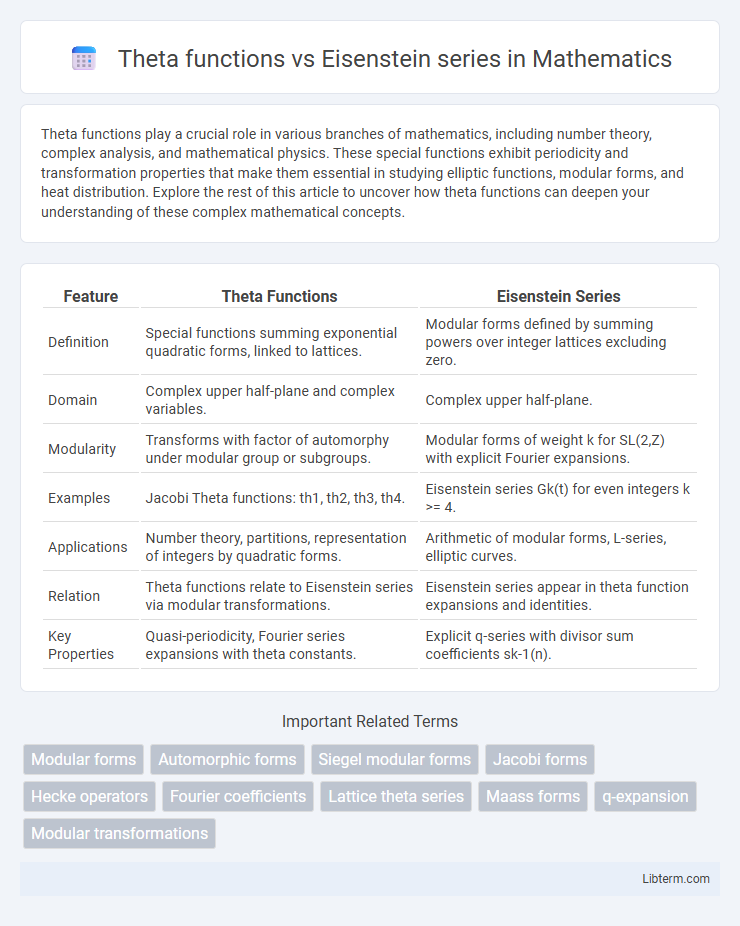
| Feature | Theta Functions | Eisenstein Series |
|---|---|---|
| Definition | Special functions summing exponential quadratic forms, linked to lattices. | Modular forms defined by summing powers over integer lattices excluding zero. |
| Domain | Complex upper half-plane and complex variables. | Complex upper half-plane. |
| Modularity | Transforms with factor of automorphy under modular group or subgroups. | Modular forms of weight k for SL(2,Z) with explicit Fourier expansions. |
| Examples | Jacobi Theta functions: th1, th2, th3, th4. | Eisenstein series Gk(t) for even integers k >= 4. |
| Applications | Number theory, partitions, representation of integers by quadratic forms. | Arithmetic of modular forms, L-series, elliptic curves. |
| Relation | Theta functions relate to Eisenstein series via modular transformations. | Eisenstein series appear in theta function expansions and identities. |
| Key Properties | Quasi-periodicity, Fourier series expansions with theta constants. | Explicit q-series with divisor sum coefficients sk-1(n). |
Introduction to Theta Functions and Eisenstein Series
Theta functions are special functions defined on the complex upper half-plane, characterized by their quasiperiodic properties and connections to lattice sums and modular forms. Eisenstein series are classical examples of modular forms constructed as infinite series summing over integer lattice points, encoding rich arithmetic information related to elliptic curves and modular groups. Both Theta functions and Eisenstein series play fundamental roles in number theory, complex analysis, and mathematical physics, serving as building blocks for more advanced modular objects.
Historical Development and Mathematical Significance
Theta functions originated in the 19th century through Jacobi's work on elliptic functions, providing a tool to study modular forms and complex analysis. Eisenstein series emerged from Eisenstein's investigations into lattice sums and modular forms, playing a crucial role in understanding the structure of modular groups and automorphic forms. Both concepts significantly contributed to modern number theory, with theta functions linking to quadratic forms and Fourier analysis, while Eisenstein series underpin the theory of modular forms and arithmetic geometry.
Fundamental Definitions and Notations
Theta functions are special functions defined by infinite series involving quadratic forms, typically expressed as \(\theta(z|\tau) = \sum_{n \in \mathbb{Z}} e^{\pi i n^2 \tau + 2 \pi i n z}\) where \(z\) is a complex variable and \(\tau\) lies in the upper half-plane. Eisenstein series are modular forms characterized by the series \(E_k(\tau) = \sum_{(m,n) \neq (0,0)} \frac{1}{(m\tau + n)^k}\) for even integers \(k > 2\), summing over integer lattice points excluding the origin. The key notation difference is that Theta functions emphasize a dependence on both \(z\) and \(\tau\) for lattice sums related to quadratic forms, while Eisenstein series focus solely on the modular parameter \(\tau\) and use a homogeneous weight \(k\) in the lattice summation.
Analytic Properties and Transformations
Theta functions exhibit modular transformation properties characterized by their behavior under the action of the Jacobi group, featuring quasiperiodicity and functional equations related to lattice sums. Eisenstein series, as automorphic forms on the modular group, possess meromorphic continuations and satisfy functional equations tied to the symmetry of the upper half-plane under SL(2,Z) transformations. Analytic properties of Theta functions emphasize their role in heat equations and Fourier expansions, while Eisenstein series are distinguished by their spectral decomposition and growth conditions at cusps.
Modular Forms: Role of Theta Functions
Theta functions serve as fundamental building blocks in the theory of modular forms, often encoding lattice structures and exhibiting transformation properties under modular groups. Unlike Eisenstein series, which are constructed from Dirichlet series and have explicit Fourier expansions with constant terms, theta functions arise from quadratic forms and display modularity through their series defined over integer lattices. Their role in modular forms includes generating spaces of cusp forms and linking to automorphic representations, thereby providing deep insights into number theory and arithmetic geometry.
Eisenstein Series as Modular Forms
Eisenstein series are a central class of modular forms characterized by their Fourier expansions and transformation behavior under the action of the modular group SL(2, Z). These series generate the space of modular forms for even weights and are instrumental in constructing the ring of modular forms, playing a key role in number theory and arithmetic geometry. Unlike theta functions, which arise from quadratic forms and lattices, Eisenstein series provide explicit analytic expressions and encode rich arithmetic information through their constant terms and special values.
Comparisons: Fourier Expansions and Representations
Theta functions and Eisenstein series both possess rich Fourier expansions, but they differ fundamentally in structure and arithmetic significance. Theta functions typically exhibit Gaussian-type exponential decay in their Fourier coefficients, reflecting their origins in quadratic forms and lattice point counting, whereas Eisenstein series have Fourier expansions with coefficients related to divisor sums and modular L-functions, encoding deep arithmetic information. Representationally, theta functions arise naturally from the Weil representation on symplectic groups, while Eisenstein series are constructed via parabolic induction from one-dimensional characters, highlighting their distinct automorphic origins.
Applications in Number Theory and Geometry
Theta functions are essential in number theory and geometry for encoding lattice point distributions and constructing modular forms, facilitating the study of quadratic forms and elliptic curves. Eisenstein series play a crucial role in the theory of modular forms, providing explicit Fourier expansions that help analyze arithmetic properties of modular curves and automorphic representations. Both objects are foundational in understanding the interplay between complex analysis, algebraic geometry, and arithmetic through their rich transformation properties and applications in counting problems and spectral theory.
Connections with Automorphic Forms
Theta functions and Eisenstein series both serve as foundational examples of automorphic forms, exhibiting modular symmetry and playing pivotal roles in number theory and representation theory. Theta functions arise from quadratic forms and encode arithmetic information through their transformation properties on the upper half-plane, while Eisenstein series are constructed via summations over lattices and provide explicit examples of non-cuspidal automorphic forms. Their interrelation is crucial in the theory of modular forms, enabling the exploration of L-functions, Fourier coefficients, and the arithmetic geometry of modular curves.
Modern Research and Open Problems
Theta functions and Eisenstein series are central objects in modern number theory and automorphic forms, with ongoing research exploring their roles in Langlands program and string theory. Current studies focus on their explicit Fourier coefficients, modularity properties, and connections to special values of L-functions, uncovering deep arithmetic and geometric structures. Open problems include understanding the full scope of their moments, the interplay with mock modular forms, and applications to higher-dimensional varieties and quantum field theory.
Theta functions Infographic
 libterm.com
libterm.com