An orthonormal basis consists of vectors that are both orthogonal and normalized, meaning each vector has a length of one and is perpendicular to all others in the set. This basis simplifies calculations in vector spaces by enabling easy projection and decomposition of vectors. Explore the full article to understand how an orthonormal basis enhances mathematical and computational techniques.
Table of Comparison
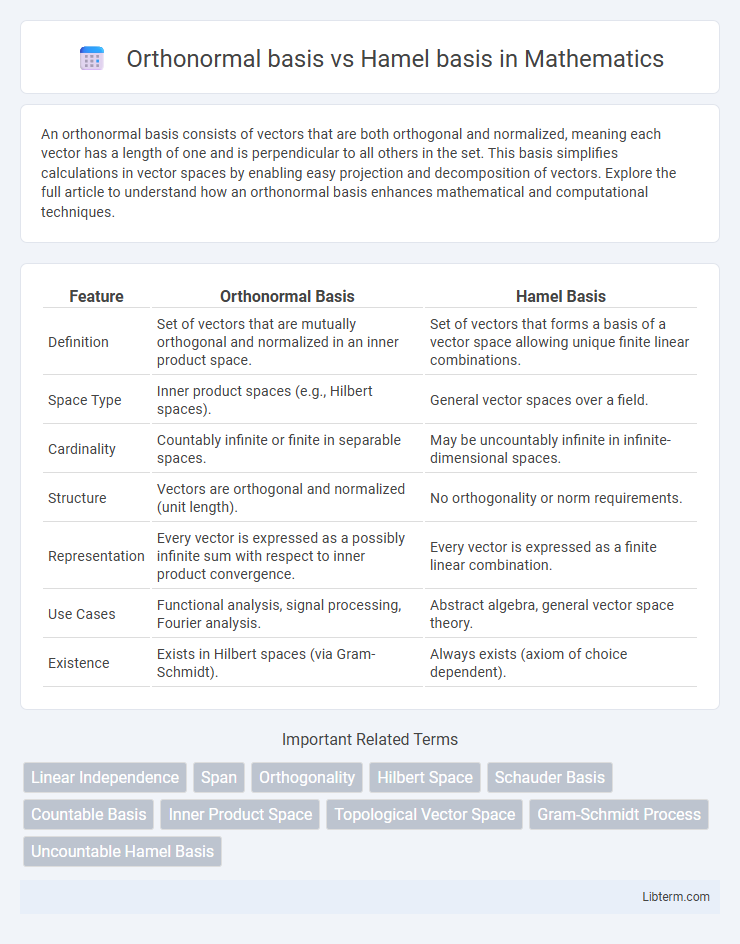
| Feature | Orthonormal Basis | Hamel Basis |
|---|---|---|
| Definition | Set of vectors that are mutually orthogonal and normalized in an inner product space. | Set of vectors that forms a basis of a vector space allowing unique finite linear combinations. |
| Space Type | Inner product spaces (e.g., Hilbert spaces). | General vector spaces over a field. |
| Cardinality | Countably infinite or finite in separable spaces. | May be uncountably infinite in infinite-dimensional spaces. |
| Structure | Vectors are orthogonal and normalized (unit length). | No orthogonality or norm requirements. |
| Representation | Every vector is expressed as a possibly infinite sum with respect to inner product convergence. | Every vector is expressed as a finite linear combination. |
| Use Cases | Functional analysis, signal processing, Fourier analysis. | Abstract algebra, general vector space theory. |
| Existence | Exists in Hilbert spaces (via Gram-Schmidt). | Always exists (axiom of choice dependent). |
Introduction to Vector Space Bases
Vector space bases serve as foundational sets of vectors that span the entire space, enabling unique vector representations. An orthonormal basis consists of vectors that are both mutually orthogonal and of unit length, simplifying computations in inner product spaces such as Euclidean spaces. In contrast, a Hamel basis, defined for general vector spaces, is a maximal linearly independent set allowing every vector to be expressed uniquely as a finite linear combination of basis elements, without requiring any geometric or orthogonality conditions.
Definition of Orthonormal Basis
An orthonormal basis is a set of vectors in a Hilbert space that are mutually orthogonal and each of unit length, allowing any vector in the space to be uniquely represented as a convergent infinite sum of these basis vectors. This concept is crucial in functional analysis and quantum mechanics because it simplifies inner product calculations and preserves vector norms. Unlike a Hamel basis, which is defined purely algebraically without considering inner products or norms, an orthonormal basis leverages geometric structure for analysis in infinite-dimensional spaces.
Definition of Hamel Basis
A Hamel basis is defined as a set of vectors in a vector space such that every element of the space can be uniquely expressed as a finite linear combination of these basis vectors. Unlike an orthonormal basis, which requires the vectors to be mutually orthogonal and of unit length in an inner product space, a Hamel basis only requires linear independence and spanning of the entire space without any metric constraints. Hamel bases exist for all vector spaces but are often infinite and non-constructive, especially in infinite-dimensional spaces, making them fundamentally different from orthonormal bases typically used in Hilbert spaces.
Key Differences Between Orthonormal and Hamel Bases
An orthonormal basis consists of vectors that are mutually orthogonal and each of unit length, enabling straightforward computation of vector components through inner products, primarily used in Hilbert spaces. A Hamel basis, or algebraic basis, is a minimal generating set such that every vector in the vector space can be uniquely expressed as a finite linear combination of basis vectors, without requiring orthogonality or norm conditions. The key difference lies in orthonormal bases exploiting inner product structure for geometric interpretation, while Hamel bases emphasize algebraic span and independence, applicable to any vector space regardless of topology.
Existence of Bases in Finite and Infinite Dimensions
In finite-dimensional vector spaces, an orthonormal basis always exists due to the Gram-Schmidt process, providing a convenient and stable way to represent vectors with respect to an inner product. Infinite-dimensional spaces may have a Hamel basis, which exists for every vector space via the axiom of choice, but such bases are typically uncountable and non-constructive, making them less practical for analysis. Orthonormal bases in infinite-dimensional Hilbert spaces form a countable set and facilitate convergence and representation, whereas Hamel bases do not guarantee these properties, highlighting the fundamental difference in their existence and utility across finite and infinite-dimensional settings.
Properties and Construction of Orthonormal Bases
Orthonormal bases consist of vectors that are both orthogonal and normalized, making them ideal for simplifying computations in inner product spaces by ensuring unit length and zero inner products between distinct vectors. Their construction relies on the Gram-Schmidt process, which systematically converts any linearly independent set into an orthonormal set while preserving the span. Unlike Hamel bases that only require linear independence, orthonormal bases enable explicit geometric interpretations and efficient expansions of vectors through inner product projections.
Properties and Construction of Hamel Bases
Hamel bases provide a vector space basis where every element can be uniquely expressed as a finite linear combination of basis vectors, contrasting with orthonormal bases that require inner product structures and usually involve infinite, countable bases in Hilbert spaces. The construction of Hamel bases relies on the axiom of choice, leading to bases that are often non-constructive and uncountably infinite for infinite-dimensional spaces. Unlike orthonormal bases, Hamel bases do not preserve length or angle properties but serve purely linear-algebraic purposes ideal for general vector spaces without inner product definitions.
Applications of Orthonormal Bases
Orthonormal bases play a crucial role in functional analysis, signal processing, and quantum mechanics by providing a framework for representing vectors as unique linear combinations of mutually orthogonal unit vectors. Their application in Fourier series and wavelet transforms enables efficient decomposition and reconstruction of functions and signals, facilitating compression and noise reduction. In contrast to Hamel bases, which exist in any vector space but are often non-constructive and infinite-dimensional without norm consistency, orthonormal bases offer computational efficiency and stability in Hilbert spaces.
Applications of Hamel Bases
Hamel bases play a crucial role in the theory of vector spaces by providing a foundation for expressing every vector as a finite linear combination of basis elements, which is essential in pure algebra and functional analysis. Unlike orthonormal bases, which are inherently linked to inner product spaces and enable efficient computations in Hilbert spaces, Hamel bases extend the notion of basis to all vector spaces, including infinite-dimensional ones without a norm or inner product. Applications of Hamel bases arise primarily in theoretical contexts such as proving the existence of linear functionals, exploring vector space dimensions, and constructing counterexamples in analysis where other bases like Schauder or orthonormal bases do not apply.
Summary and Comparative Analysis
An orthonormal basis consists of vectors that are both orthogonal and of unit length, fundamental in Hilbert spaces for simplifying inner product computations and enabling efficient projections. A Hamel basis, defined as a maximal linearly independent set spanning a vector space, applies to any vector space but often lacks orthogonality and countability, making it less practical in infinite-dimensional inner product spaces. Comparatively, orthonormal bases facilitate computational convenience and stability in functional analysis, whereas Hamel bases provide a purely algebraic framework without constraints on vector norms or angles.
Orthonormal basis Infographic
 libterm.com
libterm.com