A chaotic set represents a collection of points within a dynamical system where behavior appears random and highly sensitive to initial conditions, leading to unpredictable outcomes over time. Understanding chaotic sets is crucial for analyzing complex systems in fields such as physics, biology, and economics. Explore the rest of the article to discover how chaotic sets influence system stability and real-world applications.
Table of Comparison
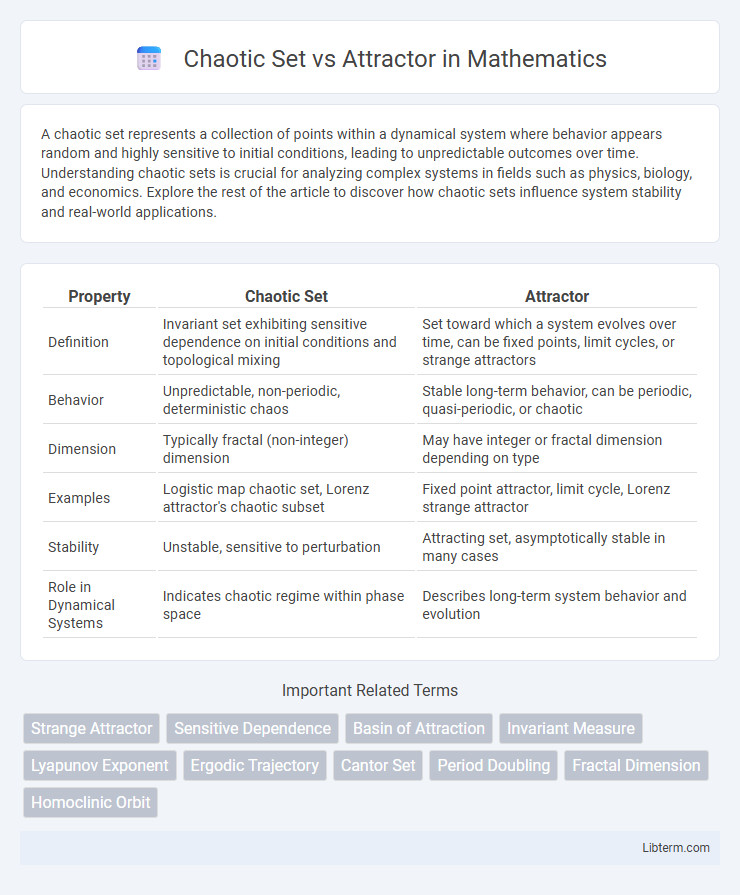
| Property | Chaotic Set | Attractor |
|---|---|---|
| Definition | Invariant set exhibiting sensitive dependence on initial conditions and topological mixing | Set toward which a system evolves over time, can be fixed points, limit cycles, or strange attractors |
| Behavior | Unpredictable, non-periodic, deterministic chaos | Stable long-term behavior, can be periodic, quasi-periodic, or chaotic |
| Dimension | Typically fractal (non-integer) dimension | May have integer or fractal dimension depending on type |
| Examples | Logistic map chaotic set, Lorenz attractor's chaotic subset | Fixed point attractor, limit cycle, Lorenz strange attractor |
| Stability | Unstable, sensitive to perturbation | Attracting set, asymptotically stable in many cases |
| Role in Dynamical Systems | Indicates chaotic regime within phase space | Describes long-term system behavior and evolution |
Understanding Chaotic Sets: A Primer
Chaotic sets are complex structures in dynamical systems characterized by sensitive dependence on initial conditions, where trajectories diverge exponentially and exhibit unpredictable long-term behavior. Unlike attractors, which are sets towards which a system evolves and stabilizes, chaotic sets do not imply steady-state convergence but represent regions of fractal geometry with dense periodic points and topological mixing. Understanding chaotic sets requires analyzing their Lyapunov exponents, fractal dimensions, and invariant measures to grasp the intricate balance between order and randomness in nonlinear dynamics.
What Is an Attractor in Dynamical Systems?
An attractor in dynamical systems is a set of numerical values toward which a system tends to evolve over time, representing long-term behavior patterns. Unlike chaotic sets that may exhibit sensitive dependence on initial conditions and complex structures, attractors can be fixed points, limit cycles, or strange attractors with fractal geometry. Understanding attractors helps predict system stability and behavior despite initial differences in dynamic states.
Key Differences Between Chaotic Sets and Attractors
Chaotic sets are complex, fractal-like structures in phase space where trajectories exhibit sensitive dependence on initial conditions and do not settle into fixed patterns. Attractors, by contrast, are subsets of phase space towards which system trajectories converge over time, representing long-term behavior such as fixed points, limit cycles, or strange attractors. The key difference lies in that chaotic sets characterize unpredictable, non-periodic motion within the system, whereas attractors define the eventual steady-state behavior or sustained dynamics that the system evolves to.
The Role of Initial Conditions
Chaotic sets exhibit sensitive dependence on initial conditions, meaning small differences in starting points lead to vastly different trajectories within the system. Attractors, including strange attractors, serve as the long-term behavior patterns toward which the system evolves despite the sensitivity to initial states. Understanding the role of initial conditions is crucial for predicting system dynamics within chaotic sets, as attractors shape the bounded regions in phase space where these trajectories converge.
Types of Attractors: Fixed Points, Limit Cycles, and Strange Attractors
Fixed points represent equilibrium states where a system remains constant, serving as simple attractors in dynamical systems. Limit cycles denote closed trajectories indicating periodic oscillations, acting as attractors for systems exhibiting repetitive behavior. Strange attractors feature fractal structures and arise in chaotic systems, capturing complex, non-repeating patterns that defy traditional periodicity and stability.
Properties of Chaotic Sets in Nonlinear Dynamics
Chaotic sets exhibit sensitive dependence on initial conditions, meaning small variations in starting points lead to vastly different trajectories in nonlinear dynamic systems. These sets are characterized by topological mixing, where any region of the set eventually overlaps with any other, ensuring complexity and unpredictability within the system's phase space. Unlike attractors, which draw trajectories toward a stable state or cycle, chaotic sets often lack such stability but still represent invariant sets that define long-term system behavior.
Visualization: Phase Space and Trajectories
Visualization of chaotic sets and attractors primarily occurs in phase space, where system trajectories reveal their dynamic behavior. Chaotic sets display sensitive dependence on initial conditions, resulting in complex, fractal-like trajectories that densely fill regions of phase space without settling into fixed points or periodic orbits. Attractors, including fixed-point, limit cycle, and strange attractors, act as the long-term destinations of trajectories, with strange attractors exhibiting fractal structure and non-periodic trajectories characteristic of chaos.
Real-World Examples of Chaotic Sets and Attractors
Chaotic sets, such as the Lorenz attractor and the Rossler attractor, exemplify complex dynamical systems with sensitive dependence on initial conditions found in climate models and fluid dynamics. Attractors like the strange attractor in weather systems demonstrate how chaotic sets evolve toward a fractal structure, describing unpredictable but bounded behavior over time. Real-world applications include modeling population dynamics in ecology and analyzing electrical circuits, where chaotic attractors reveal underlying patterns amid apparent randomness.
Mathematical Tools for Analyzing Chaos and Attraction
Chaotic sets represent regions in phase space where trajectories exhibit sensitive dependence on initial conditions, requiring mathematical tools like Lyapunov exponents and fractal dimensions to quantify their complexity and unpredictability. Attractors, including strange attractors, describe states toward which a system evolves, characterized by invariant measures and basin boundaries evaluated through Poincare maps and bifurcation analysis. Techniques such as topological entropy and recurrence plots further aid in distinguishing chaotic dynamics from regular attraction phenomena.
Implications in Science and Engineering
Chaotic sets and attractors represent fundamental concepts in dynamical systems, with chaotic sets describing regions of phase space exhibiting sensitive dependence on initial conditions and attractors representing states toward which systems evolve. The distinction impacts scientific modeling and engineering design by influencing predictability and control strategies in complex systems such as weather forecasting, fluid dynamics, and electronic circuits. Understanding chaotic attractors enables improved stability analysis and the development of robust algorithms for controlling nonlinear behavior in practical applications.
Chaotic Set Infographic
 libterm.com
libterm.com