Monomorphism in programming refers to functions or methods that operate on a single data type, enhancing code predictability and performance by reducing type complexity. It contrasts with polymorphism, where functions handle multiple types, making monomorphic code easier to optimize and debug. Explore the rest of the article to understand how monomorphism can improve your software design and efficiency.
Table of Comparison
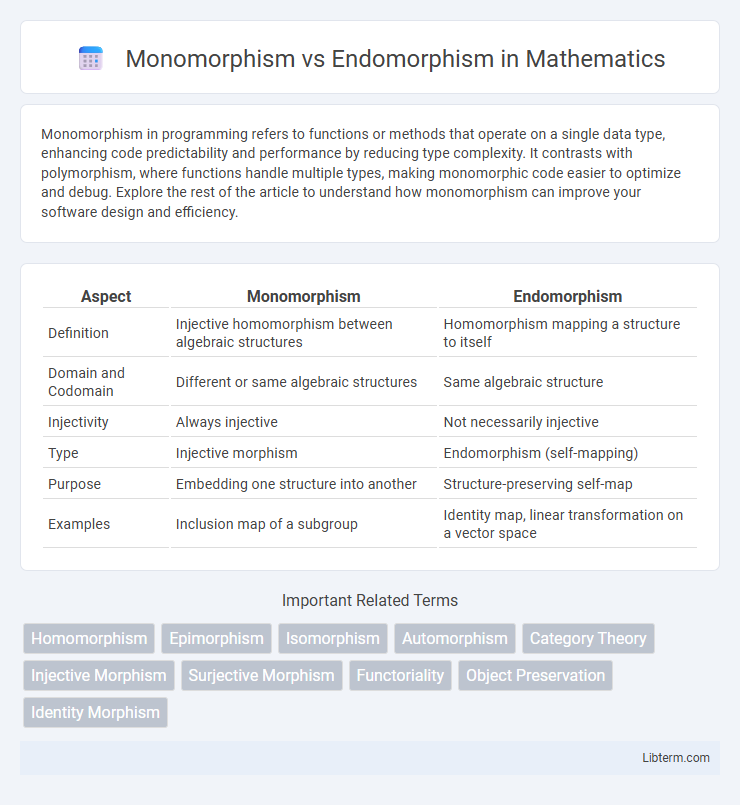
| Aspect | Monomorphism | Endomorphism |
|---|---|---|
| Definition | Injective homomorphism between algebraic structures | Homomorphism mapping a structure to itself |
| Domain and Codomain | Different or same algebraic structures | Same algebraic structure |
| Injectivity | Always injective | Not necessarily injective |
| Type | Injective morphism | Endomorphism (self-mapping) |
| Purpose | Embedding one structure into another | Structure-preserving self-map |
| Examples | Inclusion map of a subgroup | Identity map, linear transformation on a vector space |
Introduction to Monomorphism and Endomorphism
Monomorphism refers to an injective homomorphism that preserves structure by mapping distinct elements of one object to distinct elements of another within category theory. Endomorphism is a homomorphism from an object to itself, playing a critical role in defining algebraic structures like groups and rings. Understanding the distinction between monomorphisms and endomorphisms is fundamental for exploring morphisms and their properties in abstract algebra and category theory.
Defining Monomorphism in Mathematics
A monomorphism in mathematics is a morphism that is injective, meaning it preserves distinctness by mapping different elements to different images. In category theory, it generalizes the concept of injective functions, ensuring left-cancellability in compositions. Monomorphisms are fundamental in algebra and topology for identifying embeddings and structure-preserving injections.
Understanding Endomorphism Concepts
Endomorphisms are algebraic structure-preserving maps from a set to itself, playing a crucial role in fields like group theory and linear algebra. Understanding endomorphism concepts involves analyzing how these mappings maintain operations within the structure, such as preserving addition and multiplication in rings or vector spaces. Unlike monomorphisms, which are injective homomorphisms, endomorphisms may not be injective but provide insight into the internal symmetries and automorphism groups of algebraic systems.
Key Differences: Monomorphism vs Endomorphism
Monomorphism is an injective homomorphism, meaning it preserves structure while ensuring a one-to-one mapping between elements. Endomorphism is a homomorphism from a mathematical object to itself, emphasizing structure-preserving transformations within the same object. The key difference lies in monomorphisms being injective and embedding one structure into another, while endomorphisms operate internally on a single object without the injectivity requirement.
Algebraic Structures Involved
Monomorphisms in algebraic structures are injective homomorphisms preserving the structure without collapsing elements, often studied in groups, rings, and modules to understand embeddings. Endomorphisms are homomorphisms from an algebraic structure to itself, highlighting internal symmetries and structural transformations in groups, vector spaces, and monoids. The distinction lies in monomorphisms emphasizing injectivity and embedding, while endomorphisms focus on self-maps revealing automorphisms and structure-preserving operations.
Visualizing Morphisms with Examples
Monomorphisms, or injective morphisms, represent embeddings that preserve distinctness, making them ideal for visualizing injective structure-preserving maps like subset inclusions in category theory diagrams. Endomorphisms, defined as morphisms from an object to itself, illustrate internal transformations such as linear operators in vector spaces or functions on sets, often visualized by loops or arrows returning to the original object. Visual examples include monomorphisms depicted as arrows with no two elements mapping to the same target, while endomorphisms are shown as self-maps emphasizing structure-preserving self-relations.
Applications in Category Theory
Monomorphisms in category theory represent injective-like morphisms crucial for defining subobjects and embeddings, enabling the construction of limits and pullbacks in various categories like Sets and Groups. Endomorphisms, morphisms from an object to itself, facilitate the study of internal symmetries and algebraic structures such as monoids and automorphism groups within a given category. Both concepts underpin fundamental categorical constructs, with monomorphisms ensuring structural preservation and endomorphisms enabling the exploration of internal transformations and fixed points.
The Role in Abstract Algebra
Monomorphisms are injective homomorphisms that preserve algebraic structures and play a crucial role in embedding one algebraic structure into another without loss of information. Endomorphisms are homomorphisms from an algebraic structure to itself, often studied to understand internal symmetries and automorphisms within groups, rings, or modules. Both concepts help characterize structural properties and morphic behavior in categories central to abstract algebra.
Practical Implications and Use Cases
Monomorphisms ensure injective mappings preserving distinctness, crucial in database normalization and type-safe programming to prevent data loss or ambiguity. Endomorphisms, being structure-preserving functions from an object to itself, enable transformations like state transitions in automata theory and functional programming optimizations. Practical applications of monomorphisms include embedding subtypes without information loss, while endomorphisms support iterative process modeling and self-similarity in algebraic structures.
Conclusion: Choosing the Right Morphism
Choosing the right morphism depends on the structural requirements of the mathematical context; monomorphisms ensure injective mappings that preserve distinctness, while endomorphisms offer transformations within the same object, maintaining algebraic structure. Monomorphisms are ideal when embedding one structure into another without loss of information, whereas endomorphisms are suited for internal symmetries and self-maps in algebraic systems. Understanding the role and properties of each morphism guides effective application in category theory and abstract algebra.
Monomorphism Infographic
 libterm.com
libterm.com