Haar measure is a fundamental concept in mathematics, providing a way to define a measure on locally compact topological groups that is invariant under group translation. It plays a crucial role in harmonic analysis, representation theory, and probability theory by enabling integration on groups in a consistent and meaningful way. Explore this article to understand how Haar measure can be applied to diverse mathematical problems and why it is essential for your research or studies.
Table of Comparison
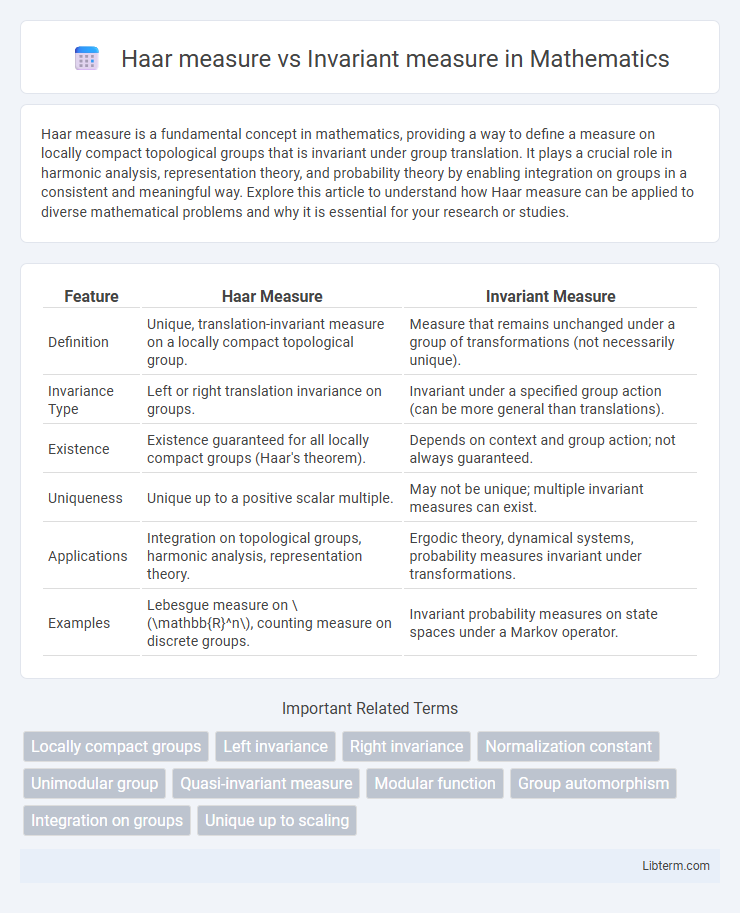
| Feature | Haar Measure | Invariant Measure |
|---|---|---|
| Definition | Unique, translation-invariant measure on a locally compact topological group. | Measure that remains unchanged under a group of transformations (not necessarily unique). |
| Invariance Type | Left or right translation invariance on groups. | Invariant under a specified group action (can be more general than translations). |
| Existence | Existence guaranteed for all locally compact groups (Haar's theorem). | Depends on context and group action; not always guaranteed. |
| Uniqueness | Unique up to a positive scalar multiple. | May not be unique; multiple invariant measures can exist. |
| Applications | Integration on topological groups, harmonic analysis, representation theory. | Ergodic theory, dynamical systems, probability measures invariant under transformations. |
| Examples | Lebesgue measure on \(\mathbb{R}^n\), counting measure on discrete groups. | Invariant probability measures on state spaces under a Markov operator. |
Introduction to Haar Measure and Invariant Measure
Haar measure is a unique translation-invariant measure defined on locally compact topological groups, fundamental for integrating functions over groups while preserving group structure. Invariant measure generalizes this concept to various group actions, maintaining measure invariance under transformations such as left or right multiplication. Understanding Haar measure is crucial for harmonic analysis and representation theory, as it ensures consistent integration on groups beyond standard Lebesgue measure.
Defining Haar Measure: Key Properties
Haar measure is a unique, translation-invariant measure defined on locally compact topological groups, assigning consistent "volume" to measurable subsets while ensuring non-negativity and regularity. It satisfies left or right invariance, meaning the measure of a set remains unchanged under group translations, and is finite on compact sets but positive on non-empty open sets. This fundamental property distinguishes Haar measure from general invariant measures, enabling integration theory and harmonic analysis on groups.
Understanding Invariant Measures in Mathematics
Invariant measures in mathematics are essential tools for analyzing symmetries within groups and spaces, ensuring measure preservation under group actions. Haar measure is a prime example of a left-invariant measure on locally compact topological groups, providing a unique, translation-invariant way to integrate functions. Understanding invariant measures involves studying their existence, uniqueness, and applications in ergodic theory, harmonic analysis, and representation theory.
Historical Context: Development of Haar Measure
The Haar measure, introduced by Alfred Haar in 1933, marked a groundbreaking advancement in measure theory by providing a unique, translation-invariant measure on locally compact topological groups. Prior to Haar's work, the existence of invariant measures was known in specific cases but lacked a unified and general theoretical framework. Haar's construction enabled rigorous integration on groups, profoundly impacting harmonic analysis, representation theory, and abstract algebra by formalizing invariant measures beyond classical Euclidean spaces.
Comparing Haar Measure and General Invariant Measures
Haar measure is a specific type of invariant measure defined on locally compact topological groups, uniquely characterized by its left-invariance and regularity, which ensures consistent integration across group elements. General invariant measures extend this concept to broader contexts, such as homogeneous spaces or transformation groups, where invariance may involve different group actions or right-invariance conditions. Comparing Haar measure and general invariant measures reveals that Haar measure serves as a fundamental building block in harmonic analysis, while invariant measures provide flexibility for studying symmetry properties in diverse mathematical structures.
Applications of Haar Measure in Harmonic Analysis
Haar measure is a unique, translation-invariant measure defined on locally compact topological groups, playing a crucial role in harmonic analysis through the integration of functions over groups. It enables the decomposition of functions into irreducible representations, facilitating the study of Fourier transforms on non-abelian groups and supporting the analysis of convolution operators. The concept of invariant measures extends beyond Haar measure, but Haar's uniqueness and existence theorem provides a fundamental tool for analyzing symmetry and group actions in various mathematical and physical contexts.
Invariant Measures in Ergodic Theory and Dynamics
Invariant measures in ergodic theory and dynamical systems play a crucial role by remaining unchanged under the action of a transformation or group. These measures enable the rigorous analysis of long-term statistical behavior of dynamical systems, facilitating the study of ergodicity, mixing properties, and recurrent phenomena. While Haar measure is a canonical, translation-invariant measure defined on locally compact groups, invariant measures in ergodic theory may arise on more general spaces and transformations, providing a broader framework for understanding dynamical invariants and statistical stability.
Existence and Uniqueness: Haar vs General Invariant Measures
Haar measure exists uniquely (up to a scalar multiple) on any locally compact topological group, providing a translation-invariant measure that is both left-invariant and right-invariant under certain conditions. General invariant measures may exist on more general spaces or groups but often lack uniqueness and might only be invariant under a subgroup or specific transformations rather than the entire group. The Haar measure's uniqueness and existence make it fundamental in harmonic analysis and representation theory, while general invariant measures are more context-dependent and typically require additional structural assumptions.
Topological Groups and Their Measures
In Topological Groups, Haar measure provides a unique, translation-invariant regular measure defined on the Borel sigma-algebra, ensuring every locally compact group admits a left-invariant measure crucial for harmonic analysis. Invariant measures generalize this concept by allowing invariance under a subgroup or specific group actions, extending applications beyond locally compact groups to non-compact or more general topological groups. The Haar measure's uniqueness up to scalar multiples distinguishes it as a fundamental tool for integrating functions over groups, while invariant measures offer flexible frameworks in ergodic theory and representation theory.
Conclusion: Implications for Mathematical Research
Haar measure provides a unique, translation-invariant measure on locally compact groups, serving as a fundamental tool in harmonic analysis and representation theory. Invariant measures extend this concept to broader contexts, including non-group actions, enabling the study of dynamical systems and ergodic theory. Understanding the distinctions and applications of these measures enhances mathematical research by facilitating the analysis of symmetry, integration on abstract spaces, and advancing fields such as group theory and functional analysis.
Haar measure Infographic
 libterm.com
libterm.com