A sheaf is a bundle of grain stalks tied together after harvesting, symbolizing abundance and agricultural efficiency. This traditional method preserves the grain while facilitating easier transportation and storage. Discover how the concept of a sheaf has evolved and its significance in agriculture by reading the full article.
Table of Comparison
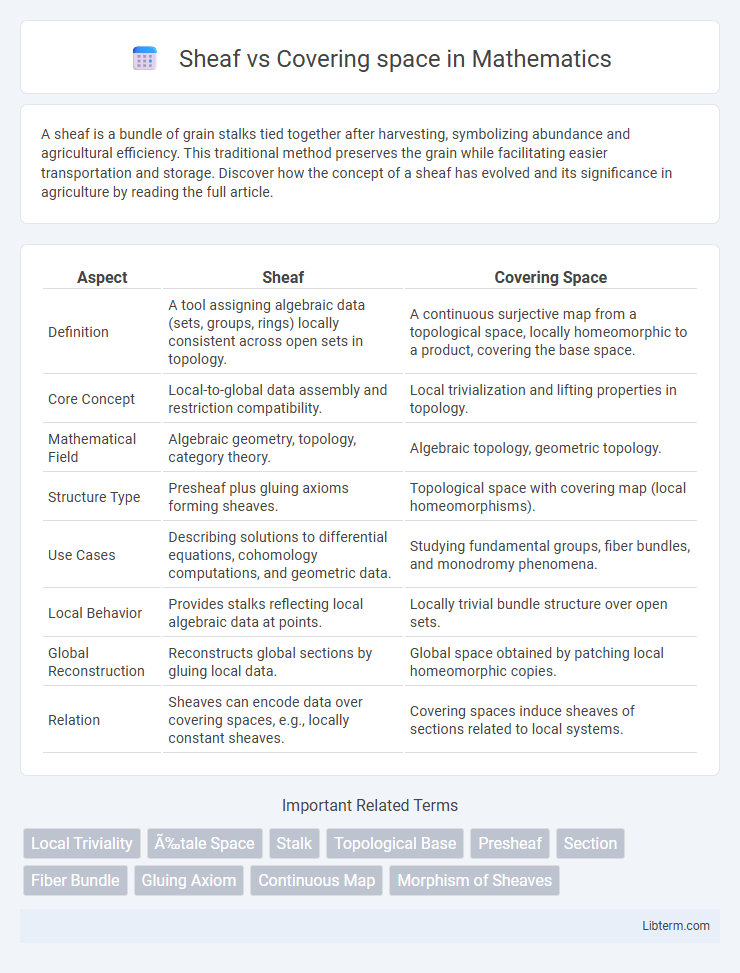
| Aspect | Sheaf | Covering Space |
|---|---|---|
| Definition | A tool assigning algebraic data (sets, groups, rings) locally consistent across open sets in topology. | A continuous surjective map from a topological space, locally homeomorphic to a product, covering the base space. |
| Core Concept | Local-to-global data assembly and restriction compatibility. | Local trivialization and lifting properties in topology. |
| Mathematical Field | Algebraic geometry, topology, category theory. | Algebraic topology, geometric topology. |
| Structure Type | Presheaf plus gluing axioms forming sheaves. | Topological space with covering map (local homeomorphisms). |
| Use Cases | Describing solutions to differential equations, cohomology computations, and geometric data. | Studying fundamental groups, fiber bundles, and monodromy phenomena. |
| Local Behavior | Provides stalks reflecting local algebraic data at points. | Locally trivial bundle structure over open sets. |
| Global Reconstruction | Reconstructs global sections by gluing local data. | Global space obtained by patching local homeomorphic copies. |
| Relation | Sheaves can encode data over covering spaces, e.g., locally constant sheaves. | Covering spaces induce sheaves of sections related to local systems. |
Introduction to Sheaves and Covering Spaces
Sheaves systematically organize local data attached to open subsets of a topological space, enabling the consistent tracking of variable structures such as functions or sections of a bundle. Covering spaces are topological spaces mapped onto a base space via a continuous surjective map, where each point has an evenly covered neighborhood resembling a discrete fiber. Understanding the interplay between sheaves and covering spaces reveals how local symmetries and algebraic structures correspond to geometric properties within algebraic topology and complex geometry.
Fundamental Concepts: Sheaves Explained
Sheaves provide a systematic framework for tracking local data attached to open sets within a topological space, ensuring consistency through restriction maps that relate data across overlapping regions. Unlike covering spaces, which represent global geometric structures by mapping one topological space over another with discrete fibers, sheaves encapsulate how local properties and functions vary continuously, enabling powerful tools in algebraic geometry and topology. The fundamental concept of a sheaf lies in its ability to glue compatible local sections into global sections, reflecting the intricate interplay between local and global phenomena in mathematical spaces.
Understanding Covering Spaces: A Primer
Understanding covering spaces involves analyzing continuous surjective maps p: E - B, where each point in the base space B has an open neighborhood U such that p^(-1)(U) is a disjoint union of open sets in E, each homeomorphic to U. This local triviality condition allows for studying the fundamental group p_1(B) through lifting properties and monodromy representations. Sheaves, in contrast, systematically organize local data and morphisms, often encoding continuous functions or sections, but lack the homotopical lifting structure intrinsic to covering spaces.
Key Differences Between Sheaves and Covering Spaces
Sheaves assign algebraic structures like sets, groups, or rings to open subsets of a topological space with consistency under restriction, while covering spaces consist of a continuous surjective map from one space onto another, locally homeomorphic to the base space. Sheaves capture local-to-global data organization through stalks and sections, whereas covering spaces emphasize topological lifting properties and path connectivity. The fundamental difference lies in sheaves' focus on variable algebraic data over opens versus covering spaces' emphasis on topological structure and fiber behavior.
Similarities and Interconnections
Sheaves and covering spaces both facilitate the local-to-global transition in topology by encoding local data coherently over a base space. A covering space corresponds to a locally trivial fiber bundle with discrete fibers, while a sheaf assigns data, such as sets, groups, or rings, to open sets satisfying locality and gluing axioms. The etale space construction reveals their interconnection by representing a sheaf as a space with a local homeomorphism onto the base, effectively linking sheaves and covering spaces through continuous local sections.
Algebraic Topology Perspective
Sheaves and covering spaces serve as fundamental tools in algebraic topology for understanding local-to-global phenomena on topological spaces. A covering space provides a geometric framework by locally resembling a product space, enabling the study of fundamental groups through deck transformations and liftings, while sheaves abstractly encode local data and their gluing conditions across open sets via category theory. The interplay between these concepts arises in classifying covering spaces via the fundamental groupoid, where sheaf cohomology detects obstructions to global sections, bridging geometric intuition with algebraic formalism.
Applications of Sheaves in Mathematics
Sheaves provide a powerful framework for systematically tracking local data glued together to form global structures, crucial in algebraic geometry, differential geometry, and topology. They facilitate the study of solutions to systems of partial differential equations and the cohomological analysis of complex manifolds, enabling deeper insights into the structure of spaces beyond the capabilities of covering spaces. Applications include defining cohomology theories, characterizing fiber bundles, and addressing problems in deformation theory and moduli spaces.
Covering Spaces in Topological Studies
Covering spaces are fundamental constructs in algebraic topology, serving as continuous surjective maps from a covering space to a base space, where each point in the base has a neighborhood evenly covered by the map. They facilitate the study of fundamental groups by providing a geometric interpretation of group actions and enabling the classification of covering maps via subgroup correspondence. Unlike sheaves, which systematize local data across open sets, covering spaces emphasize the global topological structure, allowing for the analysis of path lifting, homotopy lifting properties, and the construction of universal covers.
Sheaf Theory and Covering Space Theory in Modern Research
Sheaf theory provides a framework to systematically track locally defined algebraic or topological data across spaces, enabling refined classification of geometric and analytic structures in modern research. Covering space theory explores continuous surjective maps that reveal global topological properties through local homeomorphisms, playing a critical role in understanding fundamental groups and fiber bundles. Recent studies integrate sheaf-theoretic methods with covering space concepts to address complex problems in algebraic geometry, topology, and mathematical physics, enhancing tools for cohomology, descent theory, and homotopy theory.
Summary and Future Directions
Sheaf theory generalizes the concept of covering spaces by encoding local data with algebraic structures, facilitating advanced tools in algebraic geometry and topology. Future research aims to deepen the interplay between sheaf cohomology and higher-dimensional covering spaces to enhance classification techniques and computational methods. Advancements in derived sheaf theory and homotopical perspectives promise to expand applications in modern mathematics and theoretical physics.
Sheaf Infographic
 libterm.com
libterm.com