An open set is a fundamental concept in topology and mathematics, defined as a set where every point has a neighborhood entirely contained within the set. Understanding the properties of open sets helps you grasp continuity, convergence, and other key ideas in analysis. Explore the rest of the article to deepen your knowledge of open sets and their applications.
Table of Comparison
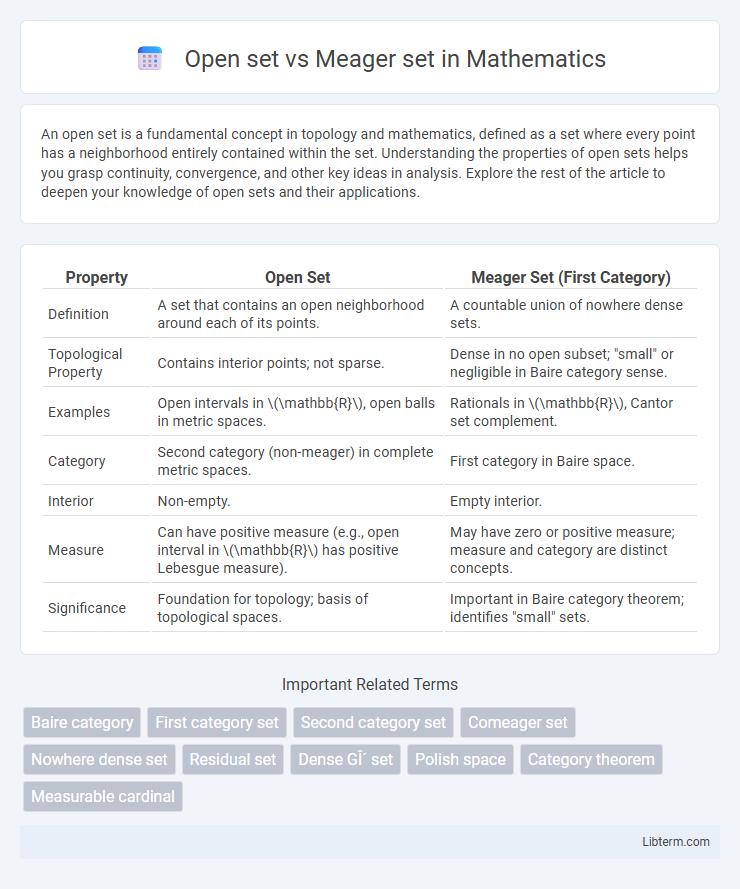
| Property | Open Set | Meager Set (First Category) |
|---|---|---|
| Definition | A set that contains an open neighborhood around each of its points. | A countable union of nowhere dense sets. |
| Topological Property | Contains interior points; not sparse. | Dense in no open subset; "small" or negligible in Baire category sense. |
| Examples | Open intervals in \(\mathbb{R}\), open balls in metric spaces. | Rationals in \(\mathbb{R}\), Cantor set complement. |
| Category | Second category (non-meager) in complete metric spaces. | First category in Baire space. |
| Interior | Non-empty. | Empty interior. |
| Measure | Can have positive measure (e.g., open interval in \(\mathbb{R}\) has positive Lebesgue measure). | May have zero or positive measure; measure and category are distinct concepts. |
| Significance | Foundation for topology; basis of topological spaces. | Important in Baire category theorem; identifies "small" sets. |
Introduction to Open Sets and Meager Sets
Open sets, fundamental in topology, are defined as collections of points where every point possesses a neighborhood fully contained within the set, forming the basis for continuity and convergence. Meager sets, also known as sets of the first category, are countable unions of nowhere dense sets and represent "small" or "thin" subsets within a topological space. Understanding the contrast between open sets, which are "large" and contain interior points, and meager sets, which are "small" and lack substantial interior structure, is crucial in advanced analysis and descriptive set theory.
Fundamental Concepts in Topology
Open sets form the backbone of topology, defining the structure through collections of neighborhoods that satisfy union and finite intersection properties. Meager sets, also known as sets of the first category, are countable unions of nowhere dense sets and represent "small" or "negligible" subsets in a topological space. Understanding the distinction between open and meager sets is crucial for analyzing Baire category theorem applications and the interplay between "large" and "small" sets in topology.
Definition of Open Sets
Open sets are fundamental constructs in topology, defined as collections of points in a space where each point has a neighborhood fully contained within the set, ensuring no boundary points are included. This property guarantees that open sets serve as building blocks for defining continuity, convergence, and topological structures. Contrasting with meager sets, which are countable unions of nowhere dense sets and often considered "small" or "thin," open sets are typically "large" and robust within the topological space.
Understanding Meager Sets
A meager set, also known as a set of first category, is a countable union of nowhere dense subsets in a topological space, meaning it is "small" in the sense of category and lacks interior points. Unlike open sets, which contain an open neighborhood around each point, meager sets are "thin" and do not contain any open subsets, making them negligible in Baire category theory. Understanding meager sets is crucial in functional analysis and topology, as they represent exceptions in spaces where typical properties hold on residual (non-meager) sets.
Key Properties of Open Sets
Open sets in topology are characterized by containing none of their boundary points, ensuring every point within has a neighborhood entirely contained in the set. These sets are fundamentally used to define continuous functions, where the preimage of an open set under a function remains open. Open sets form the basis for topological spaces, enabling the definition of convergence, connectedness, and compactness in analysis.
Key Properties of Meager Sets
Meager sets, also known as sets of first category, are defined as countable unions of nowhere dense sets in a given topological space, contrasting with open sets which contain at least one non-empty open subset. Key properties of meager sets include their topological smallness, as they are negligible in the sense of Baire category, meaning their complement is dense in a complete metric space. Meager sets are preserved under countable unions and subsets, but unlike open sets, they lack interior points, highlighting their sparse distribution within the space.
Differences Between Open Sets and Meager Sets
Open sets are defined as collections of points where each point has a neighborhood entirely contained within the set, emphasizing local completeness in topological spaces. Meager sets, also known as sets of first category, are countable unions of nowhere dense sets and are considered small or negligible in terms of Baire category. The key difference lies in openness versus scarcity: open sets possess interior points forming robust structures, whereas meager sets lack interior and are topologically thin or sparse.
Examples Illustrating Open and Meager Sets
An open set in a topological space, such as the interval (0,1) in the real numbers, contains all its interior points, allowing a small neighborhood around each point within the set. A meager set, exemplified by the rationals within the real line, is a countable union of nowhere dense sets, meaning it is "small" or "thin" in the sense of category and lacks any intervals. The Cantor set serves as a classic example of a closed, nowhere dense set that is meager, contrasting the robust structure of open sets in real analysis.
Applications in Real Analysis and Topology
Open sets form the foundation for defining continuity, convergence, and topological properties in real analysis and general topology, enabling the characterization of neighborhoods and the structure of metric spaces. Meager sets, also known as sets of the first category, are crucial in Baire category theory, where they help distinguish "large" sets from "small" or negligible ones, impacting functional analysis and the study of generic properties. Applications include proving the Baire category theorem, understanding nowhere dense sets, and analyzing typical behavior in complete metric spaces and function spaces.
Conclusion and Summary
Open sets are fundamental in topology, characterized by containing none of their boundary points, whereas meager sets, also known as sets of the first category, are countable unions of nowhere dense sets and often considered "small" or negligible in a topological space. The distinction highlights the interplay between "largeness" in terms of topological interior (open sets) and "smallness" in terms of topological structure complexity (meager sets). Understanding this contrast is crucial for grasping key concepts in Baire category theory and its applications across analysis and topology.
Open set Infographic
 libterm.com
libterm.com