Minimal surfaces are geometric shapes that locally minimize surface area, often characterized by zero mean curvature. These surfaces appear in various fields such as architecture, physics, and materials science for their efficiency and aesthetic appeal. Discover how minimal surfaces can influence your understanding of geometry and design in the rest of this article.
Table of Comparison
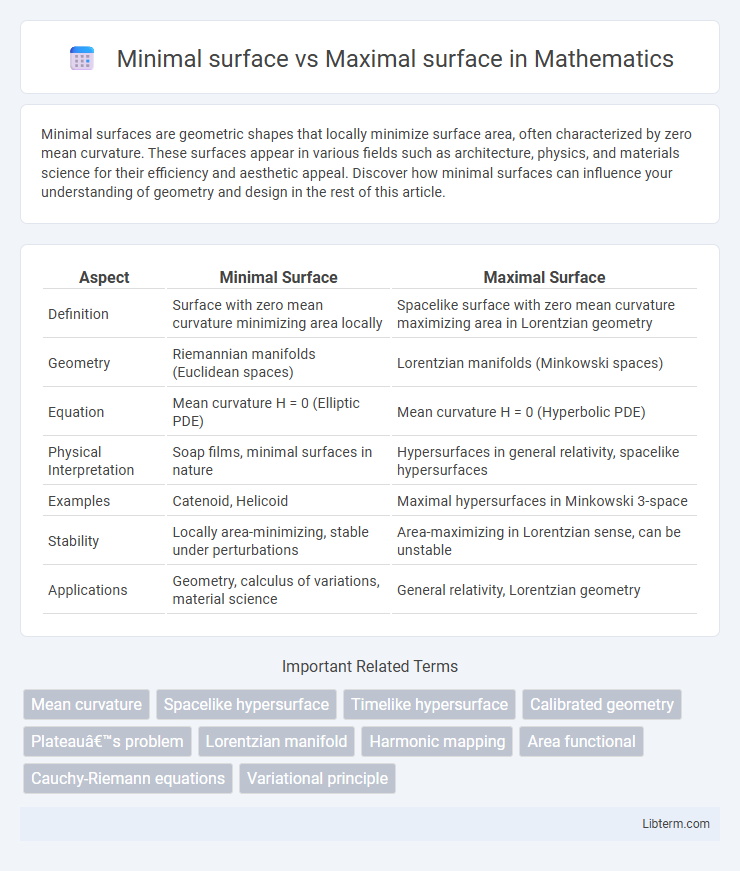
| Aspect | Minimal Surface | Maximal Surface |
|---|---|---|
| Definition | Surface with zero mean curvature minimizing area locally | Spacelike surface with zero mean curvature maximizing area in Lorentzian geometry |
| Geometry | Riemannian manifolds (Euclidean spaces) | Lorentzian manifolds (Minkowski spaces) |
| Equation | Mean curvature H = 0 (Elliptic PDE) | Mean curvature H = 0 (Hyperbolic PDE) |
| Physical Interpretation | Soap films, minimal surfaces in nature | Hypersurfaces in general relativity, spacelike hypersurfaces |
| Examples | Catenoid, Helicoid | Maximal hypersurfaces in Minkowski 3-space |
| Stability | Locally area-minimizing, stable under perturbations | Area-maximizing in Lorentzian sense, can be unstable |
| Applications | Geometry, calculus of variations, material science | General relativity, Lorentzian geometry |
Introduction to Minimal and Maximal Surfaces
Minimal surfaces are defined as surfaces with zero mean curvature, representing the critical points of area functional and commonly modeled by soap films spanning wireframes. Maximal surfaces, conversely, arise in Lorentzian geometry with zero mean curvature but in a spacetime context, serving as analogs to minimal surfaces in Minkowski space and related to maximizing spacelike hypersurfaces. Both minimal and maximal surfaces play crucial roles in differential geometry and the calculus of variations, with applications in physics, materials science, and general relativity.
Mathematical Definition: Minimal Surface
A minimal surface is defined mathematically as a surface with mean curvature equal to zero at every point, representing a critical point for the area functional under smooth variations. It is characterized by solving the minimal surface equation, a nonlinear partial differential equation derived from the vanishing mean curvature condition. The concept plays a crucial role in differential geometry and the calculus of variations, where minimal surfaces model phenomena such as soap films spanning wireframes.
Mathematical Definition: Maximal Surface
A maximal surface in differential geometry is defined as a spacelike hypersurface with zero mean curvature in a Lorentzian manifold, often studied in the context of general relativity. It represents a critical point of the area functional under volume-preserving variations, analogous to minimal surfaces in Riemannian geometry but distinguished by the Lorentzian metric signature. Mathematically, the maximal surface satisfies the equation \(H = 0\), where \(H\) denotes the mean curvature vector, ensuring the surface locally maximizes area among nearby spacelike hypersurfaces.
Key Differences: Minimal vs Maximal Surfaces
Minimal surfaces are characterized by zero mean curvature, representing surfaces that locally minimize area, commonly seen in soap films spanning wireframes. Maximal surfaces, conversely, have zero mean curvature in Lorentzian geometry, representing spacelike surfaces that locally maximize area in spacetime models. The key difference lies in their geometric context: minimal surfaces minimize area in Euclidean spaces, while maximal surfaces maximize area within Lorentzian manifolds.
Geometric Properties and Curvature
Minimal surfaces exhibit zero mean curvature at every point, making them critical points for area functional and locally minimizing surface area. Maximal surfaces, typically defined in Lorentzian geometry, are spacelike hypersurfaces with zero mean curvature that maximize area under certain constraints in pseudo-Riemannian manifolds. The geometric distinction lies in minimal surfaces residing in Euclidean spaces with minimal area properties, whereas maximal surfaces arise in Lorentzian settings, emphasizing maximal area with timelike normal vectors and inherently different curvature behavior.
Examples of Minimal Surfaces
Examples of minimal surfaces include the catenoid, helicoid, and Enneper's surface, each characterized by zero mean curvature, which minimizes surface area locally. Minimal surfaces appear naturally in soap films spanning wireframes, demonstrating energy-efficient configurations. Their mathematical study involves calculus of variations and differential geometry, with applications in architecture and materials science.
Examples of Maximal Surfaces
Maximal surfaces are spacelike hypersurfaces in Lorentzian manifolds with zero mean curvature, often studied in the context of General Relativity and differential geometry. Classic examples include the hyperbolic paraboloid in Minkowski space and the maximal slices in the Schwarzschild spacetime that represent constant mean curvature foliations. These surfaces contrast with minimal surfaces, which are defined in Euclidean spaces as surfaces minimizing area locally, such as catenoids or helicoids.
Physical and Engineering Applications
Minimal surfaces, characterized by zero mean curvature, are crucial in architecture and materials science for designing structures with optimal stress distribution and minimal material use, such as lightweight roofs and soap films modeling. Maximal surfaces, which have maximal area properties under constraints and are less common, find applications in general relativity and cosmology for modeling spacetime geometries and optimizing surfaces under different curvature conditions. Both surfaces aid in optimizing physical systems by balancing mechanical strength, material efficiency, and geometric constraints in engineering design and scientific simulations.
Challenges in Calculation and Visualization
Minimal surfaces, characterized by zero mean curvature, present challenges in calculation due to complex nonlinear partial differential equations requiring advanced numerical methods for accurate approximation. Maximal surfaces, often studied in Lorentzian geometry with timelike mean curvature, involve hyperbolic equations that complicate stability and boundary condition treatments during computation. Visualization of minimal surfaces benefits from established geometric models and software, while maximal surfaces lack intuitive Euclidean analogs, making their representation and interpretation significantly more difficult in both academic and practical applications.
Future Research and Developments
Future research on minimal and maximal surfaces aims to deepen the understanding of their geometric properties and applications in material science and general relativity. Advanced computational techniques and machine learning models are anticipated to enhance the precision of modeling these surfaces in higher-dimensional spaces. Emerging studies focus on exploring the interplay between minimal and maximal surfaces to develop innovative optimization algorithms and novel architectural designs.
Minimal surface Infographic
 libterm.com
libterm.com