A Hausdorff space, also known as a T2 space, is a fundamental concept in topology where any two distinct points have disjoint neighborhoods, ensuring points can be "separated" by open sets. This separation property is crucial for ensuring convergence and uniqueness of limits within the space. Explore the rest of the article to understand how Hausdorff spaces influence continuity and compactness in topology.
Table of Comparison
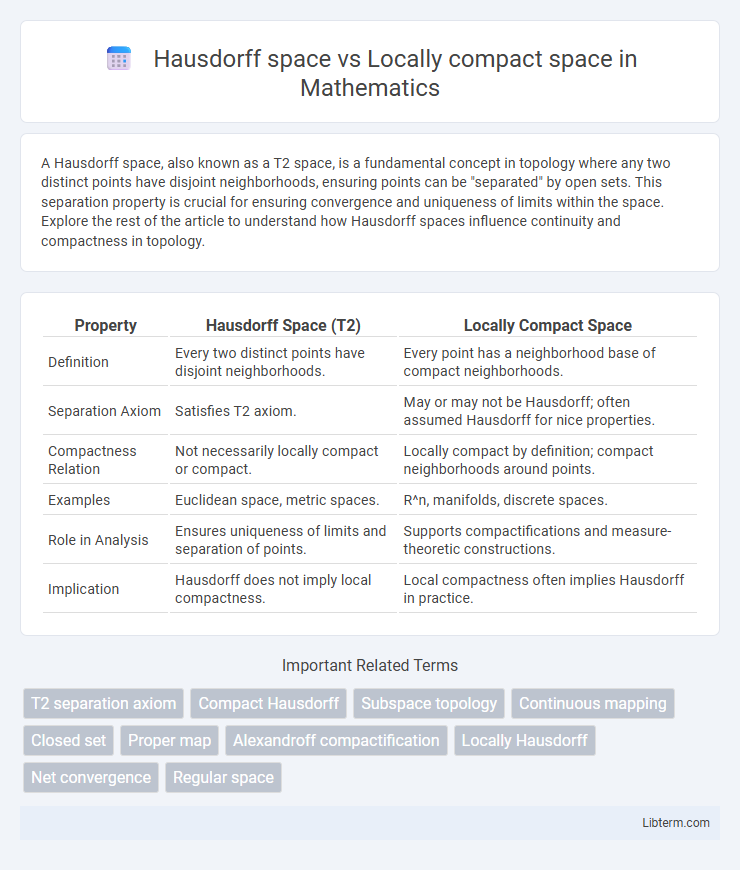
| Property | Hausdorff Space (T2) | Locally Compact Space |
|---|---|---|
| Definition | Every two distinct points have disjoint neighborhoods. | Every point has a neighborhood base of compact neighborhoods. |
| Separation Axiom | Satisfies T2 axiom. | May or may not be Hausdorff; often assumed Hausdorff for nice properties. |
| Compactness Relation | Not necessarily locally compact or compact. | Locally compact by definition; compact neighborhoods around points. |
| Examples | Euclidean space, metric spaces. | R^n, manifolds, discrete spaces. |
| Role in Analysis | Ensures uniqueness of limits and separation of points. | Supports compactifications and measure-theoretic constructions. |
| Implication | Hausdorff does not imply local compactness. | Local compactness often implies Hausdorff in practice. |
Introduction to Hausdorff and Locally Compact Spaces
Hausdorff spaces are topological spaces where any two distinct points have disjoint neighborhoods, ensuring uniqueness of limits and separation of points. Locally compact spaces are those in which every point has a neighborhood whose closure is compact, allowing for robust local analysis and facilitating the use of compactness in a localized setting. Both Hausdorff and locally compact conditions are fundamental in topology, often combined to guarantee strong separation properties and the applicability of compactness-related theorems.
Defining Hausdorff Spaces: Key Properties
Hausdorff spaces, also known as T2 spaces, are topological spaces in which any two distinct points have disjoint neighborhoods, ensuring separation and uniqueness of limits. This key property guarantees that limits of sequences, when they exist, are unique, making Hausdorff spaces central in analysis and topology. Unlike locally compact spaces, which require every point to have a compact neighborhood, Hausdorff spaces do not impose compactness conditions but emphasize point separation.
Locally Compact Spaces: Formal Definition
Locally compact spaces are topological spaces in which every point has a neighborhood whose closure is compact, providing a crucial bridge between compactness and general topological properties. Formally, a space \(X\) is locally compact if for every point \(x \in X\), there exists an open set \(U\) containing \(x\) such that the closure \(\overline{U}\) is compact in \(X\). This definition plays a significant role in analysis, especially in the study of continuous functions and measure theory, where local compactness facilitates the extension of compact space results.
Distinguishing Features: Hausdorff vs Locally Compact
Hausdorff spaces require that any two distinct points have disjoint neighborhoods, ensuring unique limits of sequences or nets. Locally compact spaces further demand that every point has a neighborhood whose closure is compact, combining local compactness with the separation property. While all locally compact Hausdorff spaces are Hausdorff, the converse is not true; Hausdorff spaces need not have local compactness.
Examples of Hausdorff Spaces
Hausdorff spaces include familiar examples such as Euclidean spaces \(\mathbb{R}^n\) where distinct points have disjoint neighborhoods, satisfying the T2 separation axiom. Another example is any metric space, such as the discrete space where each singleton set is open, thereby ensuring Hausdorff property. While all locally compact Hausdorff spaces are Hausdorff, examples like the closed interval \([0,1]\) are both locally compact and Hausdorff, demonstrating the intersection of these topological properties.
Examples of Locally Compact Spaces
Locally compact spaces include Euclidean spaces \(\mathbb{R}^n\), where every point has a compact neighborhood such as closed balls, and discrete spaces, where singletons are compact neighborhoods. Unlike general Hausdorff spaces that only require distinct points to be separated by neighborhoods, locally compact spaces must have neighborhoods whose closure is compact, making spaces like the real line with usual topology a prime example. Other examples include open subsets of \(\mathbb{R}^n\) and manifolds without boundary, illustrating the importance of local compactness in analysis and topology.
Interplay: When are Locally Compact Spaces Hausdorff?
Locally compact spaces are Hausdorff if they satisfy the T2 separation axiom, ensuring every pair of distinct points have disjoint neighborhoods. This interplay is critical in topology since the Hausdorff condition guarantees unique limits of sequences, while local compactness provides compact neighborhoods around points. Commonly, locally compact Hausdorff spaces form the foundation for advanced concepts like the one-point compactification and Radon measures.
Topological Implications of Hausdorff and Local Compactness
Hausdorff spaces ensure unique limits of sequences, crucial for well-defined convergence and separation of points, while locally compact spaces guarantee each point has a neighborhood with compact closure, enabling powerful compactness arguments in analysis. The intersection of these properties allows the construction of one-point compactifications, facilitating the extension of continuous functions and enhancing topological compactness features. Locally compact Hausdorff spaces provide the ideal setting for studying measure theory and harmonic analysis due to their balanced separation and compactness characteristics.
Applications in Mathematics and Analysis
Hausdorff spaces play a crucial role in topology by guaranteeing the uniqueness of limits, which is essential in functional analysis and differential geometry for defining well-behaved continuous functions and manifolds. Locally compact spaces are fundamental in harmonic analysis and measure theory, enabling the application of the Riesz representation theorem and the construction of Haar measures on locally compact groups. Both spaces form the backbone of modern analysis frameworks, with Hausdorff conditions ensuring separation properties and local compactness providing compact neighborhoods necessary for integrating and approximating functions.
Summary: Comparing Hausdorff and Locally Compact Spaces
Hausdorff spaces ensure that any two distinct points have disjoint neighborhoods, providing a strong separation condition essential in topology. Locally compact spaces require every point to have a compact neighborhood, enabling refined analysis in areas such as functional analysis and harmonic analysis. While all locally compact spaces are Hausdorff in common contexts, the reverse is not true, highlighting their distinct roles in topological structure and compactness properties.
Hausdorff space Infographic
 libterm.com
libterm.com