A commutative diagram visually represents mathematical structures and their relationships, ensuring that all directed paths with the same start and endpoints yield equivalent results. These diagrams are essential tools in category theory and algebra for demonstrating how functions or morphisms compose consistently. Explore the rest of the article to deepen your understanding of commutative diagrams and their applications.
Table of Comparison
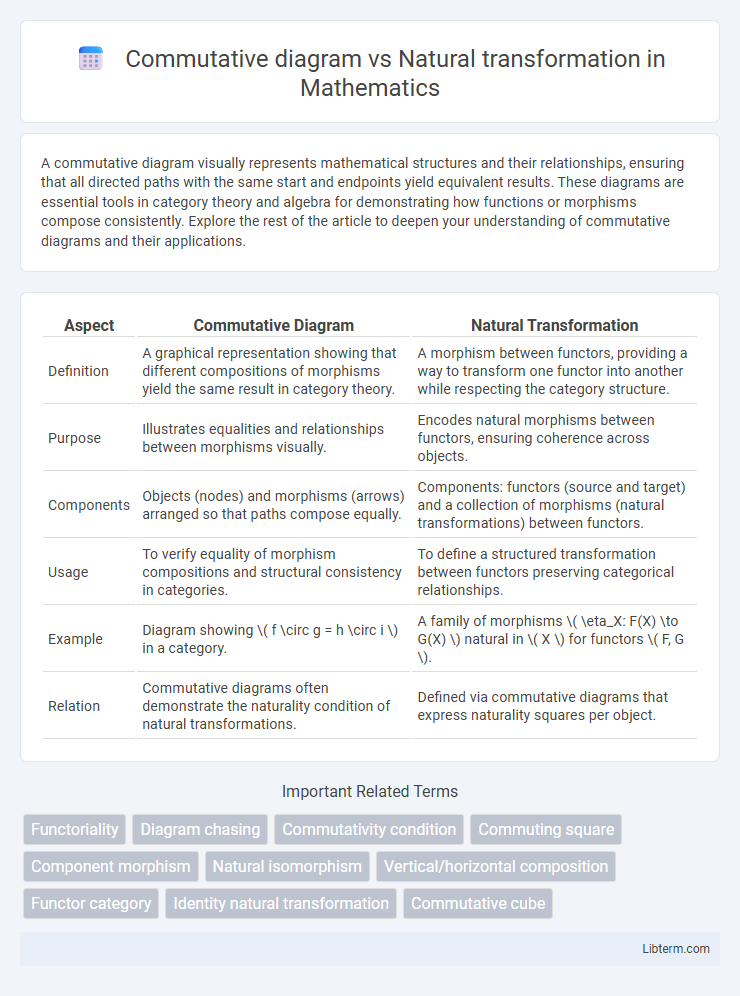
| Aspect | Commutative Diagram | Natural Transformation |
|---|---|---|
| Definition | A graphical representation showing that different compositions of morphisms yield the same result in category theory. | A morphism between functors, providing a way to transform one functor into another while respecting the category structure. |
| Purpose | Illustrates equalities and relationships between morphisms visually. | Encodes natural morphisms between functors, ensuring coherence across objects. |
| Components | Objects (nodes) and morphisms (arrows) arranged so that paths compose equally. | Components: functors (source and target) and a collection of morphisms (natural transformations) between functors. |
| Usage | To verify equality of morphism compositions and structural consistency in categories. | To define a structured transformation between functors preserving categorical relationships. |
| Example | Diagram showing \( f \circ g = h \circ i \) in a category. | A family of morphisms \( \eta_X: F(X) \to G(X) \) natural in \( X \) for functors \( F, G \). |
| Relation | Commutative diagrams often demonstrate the naturality condition of natural transformations. | Defined via commutative diagrams that express naturality squares per object. |
Introduction to Commutative Diagrams
Commutative diagrams visually represent the equality of composed morphisms in category theory, ensuring that different paths between objects yield the same result. They serve as fundamental tools for illustrating properties like functoriality and naturality without relying solely on symbolic equations. These diagrams provide an intuitive framework for understanding complex structures and transformations within mathematical categories.
Understanding Natural Transformations
Natural transformations provide a framework to compare functors by assigning morphisms between their images while preserving categorical structure. Unlike commutative diagrams, which visually verify equality of composed morphisms, natural transformations capture systematic ways to transform one functor into another coherently across all objects. Understanding natural transformations is crucial for grasping higher-level category theory concepts such as functor categories and adjunctions.
Key Concepts in Category Theory
Commutative diagrams visually represent equations between morphisms in category theory, ensuring paths with the same start and endpoint yield identical results, which is fundamental for expressing relationships between objects and morphisms. Natural transformations provide a formal way to relate functors, defining a morphism between functors that respects the structure of categories involved, capturing the idea of "naturality" across all objects. Both concepts are essential for understanding functorial relationships and coherence conditions within categorical frameworks, with commutative diagrams often used to illustrate natural transformations explicitly.
Visual Representation: Commutative Diagrams Explained
Commutative diagrams visually represent relationships between objects and morphisms in category theory, illustrating how different paths yield the same result, ensuring diagrammatic consistency. Natural transformations extend this concept by providing a systematic way to compare functors through component morphisms that respect the structure of categories involved. The clarity of commutative diagrams makes them essential for understanding the coherence conditions crucial to natural transformations.
Defining Natural Transformations with Examples
Natural transformations provide a way to map between functors while preserving the compositional structure, illustrated by commutative diagrams that demonstrate consistent transformations across all objects in a category. For example, given two functors \(F, G: \mathcal{C} \to \mathcal{D}\), a natural transformation \(\eta: F \Rightarrow G\) assigns to each object \(X\) in \(\mathcal{C}\) a morphism \(\eta_X: F(X) \to G(X)\) in \(\mathcal{D}\) such that for every morphism \(f: X \to Y\) in \(\mathcal{C}\), the square involving \(F(f), G(f), \eta_X, \eta_Y\) commutes. This commutative diagram is critical because it visually confirms the naturality condition, ensuring the transformation respects the functorial structure across all morphisms.
Differences between Commutative Diagrams and Natural Transformations
Commutative diagrams visually represent equations between morphisms in category theory, ensuring that all directed paths with the same start and endpoints compose to the same morphism. Natural transformations provide a structured way to map between functors, consisting of a family of morphisms that satisfy a naturality condition expressed through commutative diagrams. The key difference lies in their roles: commutative diagrams illustrate consistency in morphism compositions, while natural transformations define systematic relationships between functors across categories.
The Role of Commutative Diagrams in Mathematics
Commutative diagrams serve as a visual and structural tool in mathematics to represent and verify relationships between objects and morphisms, ensuring that different paths yield the same result. They play a crucial role in category theory by illustrating the coherence conditions that natural transformations must satisfy, making abstract concepts more tangible and easier to reason about. By encapsulating complex functional compositions and transformations, commutative diagrams provide clarity and rigor in proofs involving natural transformations and other categorical constructs.
Applications of Natural Transformations in Category Theory
Natural transformations play a crucial role in category theory by providing a way to compare functors and establish coherence between different constructions, enabling the definition of equivalences between categories. Their applications include the formulation of adjoint functors, representation of limits and colimits, and the characterization of universal properties, which cannot be fully captured by commutative diagrams alone. Unlike commutative diagrams that visualize object and morphism relationships in a fixed setting, natural transformations offer a more flexible and fundamental tool for expressing morphisms between functors and facilitating higher-level categorical abstractions.
Interconnections: When Commutative Diagrams Encode Natural Transformations
Commutative diagrams visually represent the relationships between functors and natural transformations, encoding how these transformations preserve structure between categories. Natural transformations arise when each component of the diagram commutes, ensuring that for every object, the morphisms mapped by functors align consistently. This interconnection allows categorical concepts to be expressed diagrammatically, providing an intuitive framework for understanding complex functional relations in category theory.
Summary: Choosing Between Commutative Diagrams and Natural Transformations
Commutative diagrams visually represent relationships between objects and morphisms in category theory, making them ideal for demonstrating specific equations or the equivalence of compositions. Natural transformations provide a higher-level abstraction, expressing the systematic transformation between functors and enabling the comparison of entire functorial structures rather than individual morphisms. Selecting between commutative diagrams and natural transformations depends on whether the goal is to verify exact compositional equality or to express a coherent, functor-level transformation across categories.
Commutative diagram Infographic
 libterm.com
libterm.com