A quotient space is a fundamental concept in topology formed by partitioning a space into equivalence classes and treating each class as a single point, which alters the original structure while preserving continuity. Understanding quotient spaces helps in analyzing complex topological properties and constructing new spaces from known ones. Explore this article to deepen your knowledge about quotient spaces and their applications in mathematics.
Table of Comparison
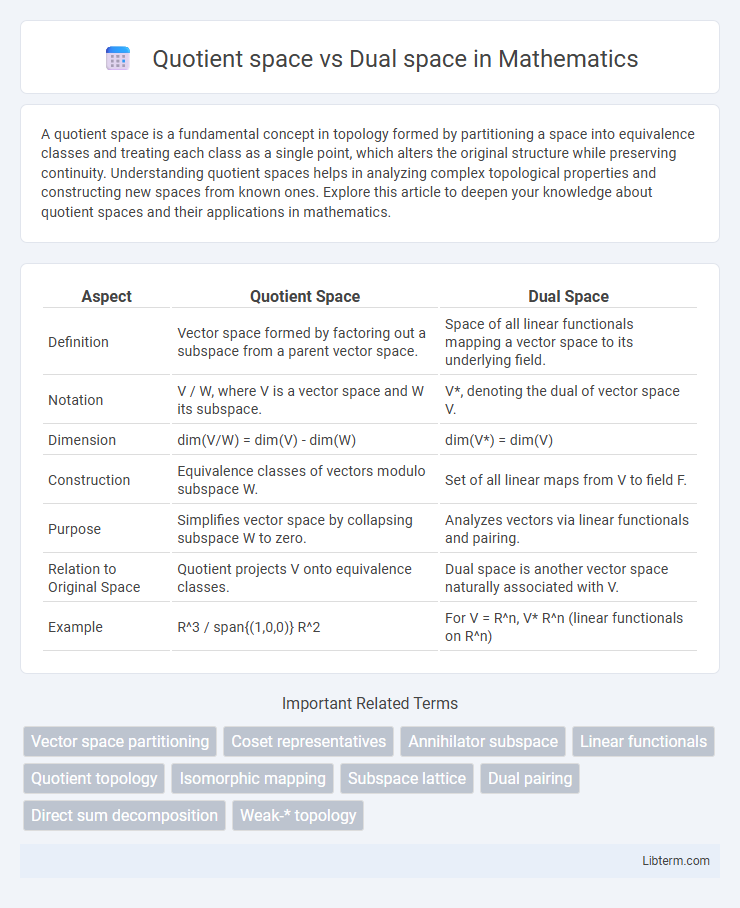
| Aspect | Quotient Space | Dual Space |
|---|---|---|
| Definition | Vector space formed by factoring out a subspace from a parent vector space. | Space of all linear functionals mapping a vector space to its underlying field. |
| Notation | V / W, where V is a vector space and W its subspace. | V*, denoting the dual of vector space V. |
| Dimension | dim(V/W) = dim(V) - dim(W) | dim(V*) = dim(V) |
| Construction | Equivalence classes of vectors modulo subspace W. | Set of all linear maps from V to field F. |
| Purpose | Simplifies vector space by collapsing subspace W to zero. | Analyzes vectors via linear functionals and pairing. |
| Relation to Original Space | Quotient projects V onto equivalence classes. | Dual space is another vector space naturally associated with V. |
| Example | R^3 / span{(1,0,0)} R^2 | For V = R^n, V* R^n (linear functionals on R^n) |
Introduction to Quotient and Dual Spaces
Quotient spaces arise by partitioning a vector space into equivalence classes formed by a subspace, effectively "collapsing" the subspace to zero and producing a new vector space structure. Dual spaces consist of all linear functionals mapping a vector space into its underlying field, capturing the action of vectors through scalar-valued functions. Understanding quotient spaces involves analyzing how vectors relate modulo a subspace, while dual spaces emphasize linear maps and their role in decomposing and reconstructing vector space behavior.
Definition of Quotient Space
A quotient space is defined as the set of equivalence classes formed by partitioning a vector space V using a subspace W, denoted as V/W, where each element corresponds to a coset v + W. This construction produces a new vector space whose elements represent vectors in V modulo W, preserving linear structure while collapsing W to the zero vector. In contrast, the dual space V* consists of all linear functionals mapping V to the underlying field, focusing on linear mappings rather than partitions of vectors.
Understanding the Dual Space
The dual space of a vector space V consists of all linear functionals mapping V to its underlying field, providing a framework to analyze V through continuous linear maps. Unlike the quotient space, which partitions V by a subspace to form equivalence classes, the dual space captures the action of vectors via linear evaluations, enabling critical applications in functional analysis and geometry. Understanding the dual space involves recognizing how it reveals the structure of V by translating vectors into scalar-valued functions, facilitating study of forms, continuity, and reflexivity properties.
Construction Processes: Quotient vs Dual
The construction of a quotient space involves partitioning a vector space by a subspace, forming equivalence classes that represent cosets of the subspace, effectively reducing the dimension by identifying vectors differing by elements of the subspace. In contrast, the dual space is built as the set of all linear functionals mapping vectors from the original space to the underlying field, capturing the algebraic action of vectors through linear evaluation. Quotient spaces emphasize factorization and equivalence under a subspace relation, while dual spaces focus on the functional perspective through continuous linear mappings.
Fundamental Properties Compared
Quotient spaces are formed by partitioning a vector space by a subspace, resulting in equivalence classes that preserve linear structure, while dual spaces consist of all continuous linear functionals mapping the original vector space to its field of scalars. Quotient spaces emphasize the geometric aspect of collapsing subspaces, characterized by surjective linear maps with kernels, whereas dual spaces highlight functional analysis properties, inherently linked to the evaluation of vectors through linear functionals. Fundamental properties such as dimension relate by the rank-nullity theorem in quotient spaces, whereas dual spaces exhibit reflexivity and norm duality in Banach space contexts.
Common Examples in Linear Algebra
Quotient spaces arise when a vector space V is partitioned by a subspace W, forming the space V/W, commonly seen in solving linear systems by factoring out solution sets of homogeneous equations. Dual spaces consist of all linear functionals mapping vectors from V to the field, exemplified by covectors in Euclidean spaces or row vectors acting on column vectors. Both concepts are fundamental in linear algebra, with quotient spaces simplifying vector spaces by equivalence relations, while dual spaces provide insights through functional evaluation and representation of linear maps.
Applications in Functional Analysis
Quotient spaces simplify the study of functional analysis by enabling the formulation of new spaces through equivalence classes, which is essential in solving partial differential equations and understanding bounded linear operators. Dual spaces provide a framework for representing continuous linear functionals, facilitating the analysis of duality, reflexivity, and weak topologies in Banach and Hilbert spaces. Together, these concepts enhance applications in optimization, spectral theory, and the study of operator algebras.
Geometric Interpretation
Quotient spaces can be viewed geometrically as the set of equivalence classes formed by collapsing a subspace to a single point, effectively creating a new space where vectors differing by an element of the subspace are identified. Dual spaces represent the collection of all linear functionals mapping vectors to scalars, providing a geometric perspective as a space of hyperplanes that separate or evaluate vectors in the original vector space. The interaction between quotient and dual spaces highlights how quotienting relates to "modding out" directions, while dual spaces capture linear constraints and forms acting on the original space.
Key Differences and Similarities
Quotient spaces and dual spaces are fundamental constructs in functional analysis with distinct roles: quotient spaces arise by partitioning a vector space via a subspace, forming equivalence classes, while dual spaces consist of all continuous linear functionals mapping vectors to the underlying field. Both structures are vector spaces, yet quotient spaces simplify original spaces by collapsing subspaces to zero, whereas dual spaces expand dimensions by representing functional actions. The interplay between quotient and dual spaces is characterized by the isometric isomorphism between the dual of a quotient space and the annihilator of the corresponding subspace in the dual space.
Conclusion and Further Reading
Quotient spaces and dual spaces serve distinct roles in functional analysis, with quotient spaces simplifying vector spaces via equivalence relations, while dual spaces consist of all continuous linear functionals on a given vector space. Understanding their interplay is crucial for advanced study in topology, normed spaces, and operator theory. For deeper insights, explore texts like Rudin's "Functional Analysis" and Conway's "A Course in Functional Analysis," which offer comprehensive treatments of these concepts and their applications.
Quotient space Infographic
 libterm.com
libterm.com