A topological basis is a collection of open sets in a topological space such that every open set can be expressed as a union of these basis elements. Understanding this concept is essential for grasping the structure and properties of different topologies. Explore the rest of the article to deepen your knowledge of topological bases and their applications.
Table of Comparison
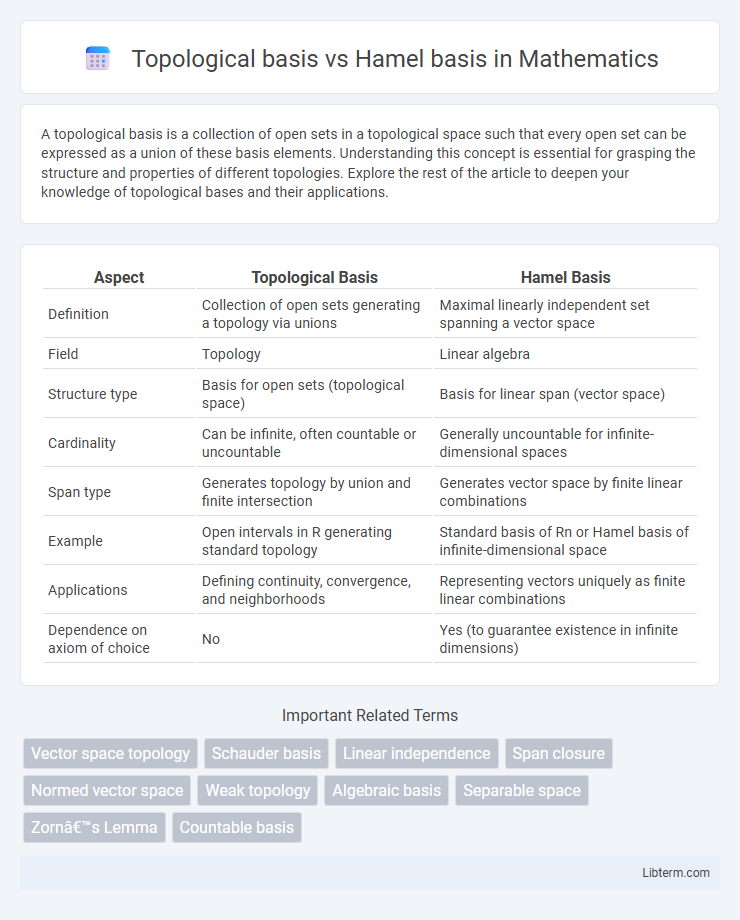
| Aspect | Topological Basis | Hamel Basis |
|---|---|---|
| Definition | Collection of open sets generating a topology via unions | Maximal linearly independent set spanning a vector space |
| Field | Topology | Linear algebra |
| Structure type | Basis for open sets (topological space) | Basis for linear span (vector space) |
| Cardinality | Can be infinite, often countable or uncountable | Generally uncountable for infinite-dimensional spaces |
| Span type | Generates topology by union and finite intersection | Generates vector space by finite linear combinations |
| Example | Open intervals in R generating standard topology | Standard basis of Rn or Hamel basis of infinite-dimensional space |
| Applications | Defining continuity, convergence, and neighborhoods | Representing vectors uniquely as finite linear combinations |
| Dependence on axiom of choice | No | Yes (to guarantee existence in infinite dimensions) |
Introduction to Bases in Mathematics
A topological basis in mathematics refers to a collection of open sets through which every open set in a topological space can be expressed as a union, essential for defining the topology's structure. A Hamel basis, in contrast, is a set of vectors in a vector space such that every vector can be uniquely represented as a finite linear combination of these basis vectors, fundamental in linear algebra. Understanding the distinction between topological and Hamel bases highlights the difference between concepts of convergence and algebraic independence in mathematical analysis and vector space theory.
Defining Topological Basis
A topological basis for a vector space equipped with a topology is a collection of open sets such that every open set can be expressed as a union of these basis elements, enabling the construction of the topology from local neighborhoods. Unlike a Hamel basis, which forms a minimal generating set for vector spaces in purely algebraic terms through linear combinations, a topological basis emphasizes the open-set structure critical for continuity and convergence. The notion of a topological basis is fundamental in functional analysis and topological vector spaces, ensuring compatibility between algebraic operations and the topological structure.
Understanding Hamel Basis
A Hamel basis is a set of vectors in a vector space such that every element can be uniquely expressed as a finite linear combination of these basis vectors, making it fundamental in algebraic vector space theory. Unlike a topological basis, which allows for infinite linear combinations and convergence in topological vector spaces like Banach or Hilbert spaces, a Hamel basis requires solely finite sums and ignores any topological considerations. The existence of a Hamel basis relies on the axiom of choice, and understanding it is essential for grasping the structure of vector spaces from an algebraic perspective rather than a topological one.
Key Differences Between Topological and Hamel Bases
A topological basis in functional analysis is a set of open sets that generate a topology, enabling convergence and continuity, whereas a Hamel basis is an algebraic concept representing a linearly independent set whose linear combinations span the entire vector space. The key difference lies in the nature of spanning: the topological basis concerns the structure of open neighborhoods for topological vector spaces, focusing on convergence properties, while the Hamel basis concerns purely algebraic spanning without regard to topology. Moreover, topological bases can be uncountable and complex, often necessary for infinite-dimensional spaces, whereas Hamel bases are typically huge and non-constructive, making them impractical for functional analysis applications.
Role of Topological Bases in Topology
Topological bases provide a framework for defining open sets and neighborhoods in a topological space, enabling the characterization of continuity, convergence, and compactness. Unlike Hamel bases, which generate vector spaces through linear combinations, topological bases rely on the intersection and union of open sets to shape the space's structure. The role of topological bases is essential in constructing and understanding various topological properties, facilitating the study of spaces in areas like analysis, geometry, and differential topology.
Hamel Basis in Vector Spaces
A Hamel basis in vector spaces is a set of vectors such that every element of the space can be uniquely expressed as a finite linear combination of these basis vectors, highlighting its algebraic nature. Unlike a topological basis, which involves convergence and infinite linear combinations in topological vector spaces, a Hamel basis emphasizes finite representations without any topological constraints. The concept of Hamel basis is fundamental in linear algebra and functional analysis for characterizing vector spaces purely algebraically.
Countability Considerations for Both Bases
A topological basis for a vector space, particularly in infinite-dimensional normed spaces, is typically uncountable due to the necessity of capturing all open sets through unions of basis elements, whereas a Hamel basis, defined purely algebraically, can be countable or uncountable depending on the vector space's dimension. Countability considerations reveal that normed spaces with a countable Hamel basis are separable, but their topological bases must often be uncountable to accommodate the topology's richness. This distinction highlights the fundamental difference between the algebraic structure of Hamel bases and the topological requirements of bases in infinite-dimensional spaces.
Examples Illustrating Topological and Hamel Bases
A topological basis in a vector space like \( C([0,1]) \) often consists of functions such as polynomials or trigonometric functions that generate the space under limits and infinite linear combinations, whereas a Hamel basis forms a minimal spanning set allowing *only* finite linear combinations without regard to topology. For example, the set of monomials \(\{1, x, x^2, \dots\}\) serves as a topological basis for continuous functions on [0,1] under the uniform norm, while the corresponding Hamel basis is uncountably infinite and cannot be explicitly constructed. This distinction highlights how topological bases facilitate approximation and convergence, whereas Hamel bases emphasize algebraic completeness without topological structure.
Applications in Functional Analysis and Topological Spaces
Topological bases underpin the study of continuity and convergence in functional analysis by providing local neighborhood structures essential for defining open sets and analyzing function spaces, particularly in normed and metric spaces. Hamel bases, consisting of algebraic linear independent vectors spanning vector spaces, serve crucial roles in the structural decomposition of infinite-dimensional vector spaces but lack direct applicability in topology due to their non-constructive nature and absence of topological properties. Functional analysts leverage topological bases for practical problem-solving in operator theory and Banach space theory, whereas Hamel bases primarily facilitate theoretical results in vector space dimension theory without influencing topological or analytic properties.
Summary: Choosing the Right Basis for Mathematical Contexts
Topological bases provide a framework for defining open sets and continuity in topological vector spaces, emphasizing convergence and neighborhood structure. Hamel bases enable vector space representation through linear independence and finite linear combinations, essential in algebraic vector space analysis. Selecting a topological basis suits functional analysis and infinite-dimensional spaces, while Hamel bases apply best in purely algebraic contexts requiring explicit vector decomposition.
Topological basis Infographic
 libterm.com
libterm.com