A simple pole is a type of singularity in complex analysis where a function behaves like 1/(z - z_0) near the point z_0, having a finite and nonzero residue. Understanding simple poles is crucial for evaluating complex integrals using the residue theorem and analyzing functions' behavior near singularities. Discover how identifying and working with simple poles can simplify your complex function analysis in the following article.
Table of Comparison
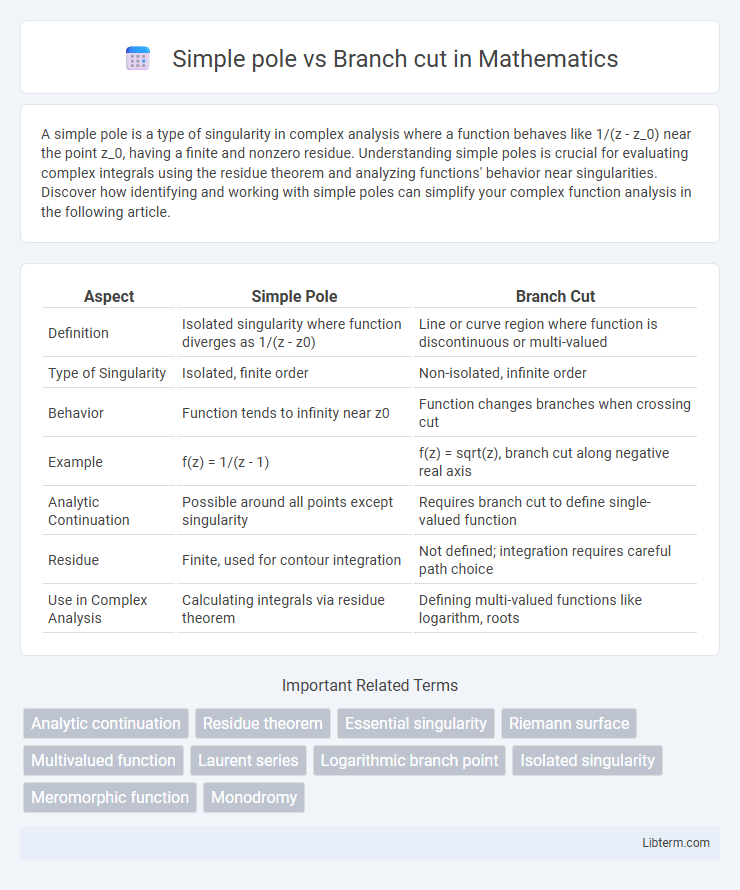
| Aspect | Simple Pole | Branch Cut |
|---|---|---|
| Definition | Isolated singularity where function diverges as 1/(z - z0) | Line or curve region where function is discontinuous or multi-valued |
| Type of Singularity | Isolated, finite order | Non-isolated, infinite order |
| Behavior | Function tends to infinity near z0 | Function changes branches when crossing cut |
| Example | f(z) = 1/(z - 1) | f(z) = sqrt(z), branch cut along negative real axis |
| Analytic Continuation | Possible around all points except singularity | Requires branch cut to define single-valued function |
| Residue | Finite, used for contour integration | Not defined; integration requires careful path choice |
| Use in Complex Analysis | Calculating integrals via residue theorem | Defining multi-valued functions like logarithm, roots |
Introduction to Poles and Branch Cuts
Poles represent isolated singularities where a complex function's value approaches infinity, typically characterized by a finite order specifying the pole's strength. Branch cuts are curves or lines in the complex plane introduced to make multi-valued functions, such as logarithms or square roots, single-valued by defining a principal branch. Understanding poles and branch cuts is essential for analyzing complex functions' behavior, especially in contour integration and analytic continuation.
Definition of Simple Pole
A simple pole is a type of isolated singularity of a complex function where the function behaves like \( \frac{1}{z - z_0} \) near the point \( z_0 \), exhibiting a finite order of one. In contrast, a branch cut is a curve or line introduced in the complex plane to make a multi-valued function single-valued by removing ambiguity. Simple poles are characterized by their residue and finite order behavior, while branch cuts are topological constructs affecting the domain of the function.
Characteristics of Simple Poles
Simple poles are isolated singularities where a complex function behaves like (z - z0)^(-1) near z0, causing the function to approach infinity in a well-defined manner. They possess a finite residue, which is crucial for evaluating contour integrals using the residue theorem in complex analysis. Unlike branch cuts that represent discontinuities across curves where multi-valued functions like logarithms are defined, simple poles characterize point singularities with predictable local behavior.
Definition of Branch Cut
A branch cut is a curve or line on the complex plane introduced to make a multi-valued function single-valued by restricting the domain. Unlike simple poles, which are isolated singularities where a function's value approaches infinity, branch cuts handle discontinuities arising from functions like logarithms or roots. Defining branch cuts ensures consistency in function values by preventing looping around branch points that would otherwise change the function's value.
Features of Branch Cuts
Branch cuts are lines or curves introduced in the complex plane to define multi-valued functions like logarithms and square roots, ensuring a consistent single-valued branch of the function. Unlike simple poles, which are isolated singularities characterized by finite-order divergences, branch cuts represent discontinuities where the function's value changes abruptly, preventing analytic continuation across the cut. These cuts are essential in contour integration and complex analysis for defining principal values and resolving ambiguities in functions with multiple branches.
Mathematical Representation
A simple pole is characterized by a singularity in a complex function where the function approaches infinity as the variable approaches a specific point, often represented mathematically as \(f(z) = \frac{a}{z - z_0} + g(z)\), with \(g(z)\) analytic near \(z_0\). Branch cuts arise in multi-valued functions such as logarithms or roots, where the domain is restricted by a curve or line segment to create a single-valued branch, formalized by defining a cut in the complex plane, for example, \(\arg(z) \in (-\pi, \pi]\) for the principal branch of \(\log(z)\). These structures differ fundamentally in their analytic nature; simple poles correspond to isolated singularities with finite-order behavior, while branch cuts reflect discontinuities necessary for the consistent definition of multi-valued functions.
Examples of Simple Poles
Simple poles occur in complex functions where the denominator has a first-order zero, such as f(z) = 1/(z - a), which has a simple pole at z = a. Another example is the function g(z) = (z + 2)/((z - 1)(z - 3)), which possesses simple poles at z = 1 and z = 3. Unlike branch cuts that represent multi-valued function discontinuities, simple poles correspond to isolated singularities with finite residues used in contour integration.
Examples of Branch Cuts
Branch cuts are introduced in complex analysis to define multi-valued functions like the complex logarithm or square root, enabling a single-valued branch by removing a curve from the complex plane. A common example is the principal branch of the complex logarithm, which uses a branch cut along the negative real axis to exclude the discontinuity caused by the function's argument changing by 2p. Another example is the complex square root function, where the branch cut is often taken along the negative real axis to avoid ambiguity in defining the angle, creating a domain where the function is continuous and single-valued.
Key Differences: Simple Pole vs Branch Cut
A simple pole is an isolated singularity of a complex function where the function approaches infinity in a manner proportional to 1/(z - z0), characterized by a finite order. A branch cut is a curve or line in the complex plane created to define a single-valued branch of a multi-valued function, such as logarithms or roots, preventing ambiguity around branch points. Unlike simple poles, which are isolated points with well-defined residues, branch cuts represent discontinuities along a path, making them fundamentally different types of singularities in complex analysis.
Applications in Complex Analysis
Simple poles serve as isolated singularities where functions exhibit finite-order behaviors crucial for evaluating complex integrals via residue theorem. Branch cuts enable the definition of multi-valued functions like logarithms and complex power functions by creating domains where these functions become single-valued and analytic. Applications in complex analysis include contour integration around poles for residue computations and use of branch cuts to handle functions with non-integer exponents or logarithmic discontinuities in Riemann surfaces.
Simple pole Infographic
 libterm.com
libterm.com