The Removal Lemma is a fundamental result in graph theory and combinatorics stating that if a graph contains only a small number of copies of a particular subgraph, then it can be made free of that subgraph by removing a small number of edges. This lemma has significant implications for property testing, approximation algorithms, and understanding the structure of large networks. Explore the article to learn how the Removal Lemma applies to your problems in graph analysis and theoretical computer science.
Table of Comparison
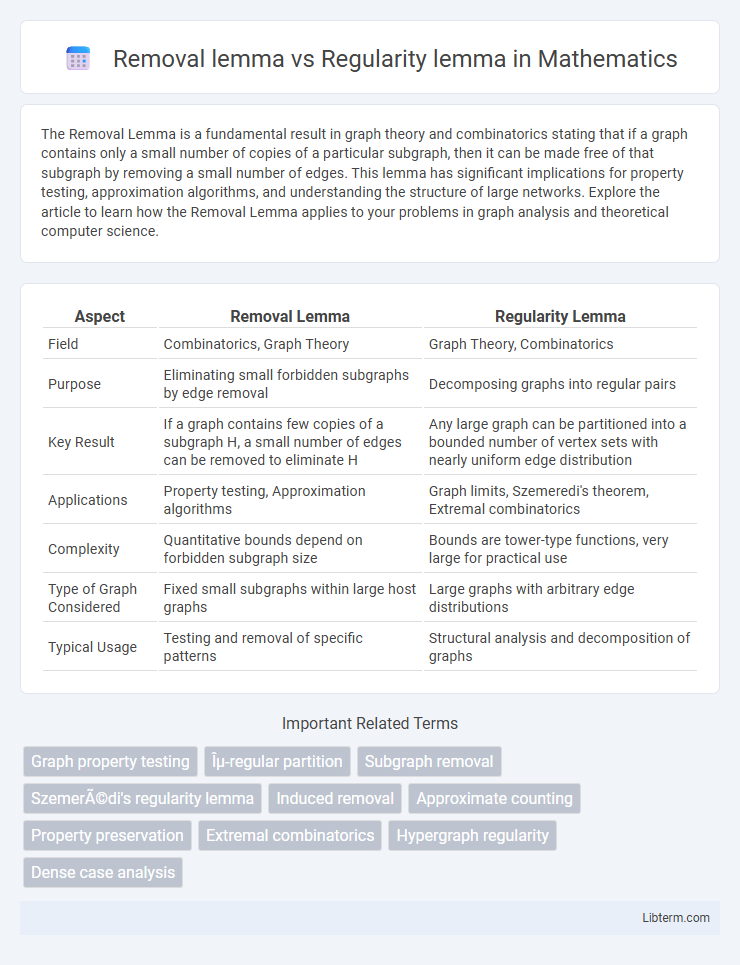
| Aspect | Removal Lemma | Regularity Lemma |
|---|---|---|
| Field | Combinatorics, Graph Theory | Graph Theory, Combinatorics |
| Purpose | Eliminating small forbidden subgraphs by edge removal | Decomposing graphs into regular pairs |
| Key Result | If a graph contains few copies of a subgraph H, a small number of edges can be removed to eliminate H | Any large graph can be partitioned into a bounded number of vertex sets with nearly uniform edge distribution |
| Applications | Property testing, Approximation algorithms | Graph limits, Szemeredi's theorem, Extremal combinatorics |
| Complexity | Quantitative bounds depend on forbidden subgraph size | Bounds are tower-type functions, very large for practical use |
| Type of Graph Considered | Fixed small subgraphs within large host graphs | Large graphs with arbitrary edge distributions |
| Typical Usage | Testing and removal of specific patterns | Structural analysis and decomposition of graphs |
Introduction to Graph Theory Lemmas
The Removal Lemma states that for any fixed subgraph H, if a graph G contains few copies of H, then removing a small number of edges eliminates all copies of H, emphasizing edge modification to achieve subgraph-freeness. The Regularity Lemma decomposes any large graph into a structured partition of vertex subsets where most pairs exhibit e-regularity, facilitating approximation of complex graphs by simpler, quasi-random structures. Together, these lemmas form foundational tools in extremal graph theory, enabling analysis of graph properties through structural and subgraph frequency perspectives.
Defining the Removal Lemma
The Removal Lemma states that for any fixed subgraph H, if a large graph G contains only a small number of copies of H, then it is possible to eliminate all copies by removing a small fraction of edges from G. This lemma provides a quantitative bridge between local subgraph structures and global graph modifications, enabling approximation of H-free graphs. It serves as a fundamental tool in extremal combinatorics, underpinning proofs related to property testing and graph limits.
Insights into the Regularity Lemma
The Regularity Lemma provides a powerful tool in graph theory by partitioning large graphs into a bounded number of random-like subgraphs, facilitating the analysis of complex structures through simpler components. Unlike the Removal Lemma, which asserts that graphs close to being free of a particular subgraph can be made strictly free by removing a small number of edges, the Regularity Lemma offers a structural decomposition that serves as the foundation for various combinatorial proofs. Insight into the Regularity Lemma reveals its crucial role in approximating arbitrary graphs with structured randomness, enabling breakthroughs in extremal graph theory and property testing.
Historical Background and Development
The Removal Lemma, first proved by Frankl, Rodl, and Rucinski in the 1980s, emerged from efforts to understand subgraph patterns and has become a cornerstone in extremal combinatorics. The Regularity Lemma, introduced by Endre Szemeredi in 1975, revolutionized graph theory by providing a powerful tool to approximate large graphs with simpler structured models. Both lemmas have evolved through extensive research, with the Removal Lemma often viewed as a consequence of the Regularity Lemma's structural insights, leading to profound advances in graph theory and additive combinatorics.
Key Differences: Removal vs Regularity Lemma
The Removal Lemma states that if a graph contains few copies of a forbidden subgraph, then removing a small number of edges eliminates all such subgraphs, emphasizing edge deletion for property enforcement. The Regularity Lemma, in contrast, partitions large graphs into a bounded number of random-like bipartite subgraphs, enabling approximate structural analysis rather than direct subgraph removal. Key differences lie in the Removal Lemma's focus on minimal edge modification to remove subgraphs versus the Regularity Lemma's role in providing a global approximate decomposition for dense graph analysis.
Applications of the Removal Lemma
The Removal Lemma is a powerful tool in graph theory and combinatorics, particularly used for property testing and proving approximate results in sparse graphs by allowing small modifications to eliminate forbidden subgraphs. It plays a critical role in algorithmic applications such as testing graph properties efficiently and finding approximate solutions to computational problems like graph coloring and subgraph isomorphism. Unlike the Regularity Lemma, which decomposes graphs into regular partitions for structural analysis, the Removal Lemma focuses on the feasibility of removing edges to destroy specific configurations, enabling wide-ranging applications in extremal combinatorics and theoretical computer science.
Applications of the Regularity Lemma
The Regularity Lemma is a fundamental tool in graph theory used to approximate large graphs by partitioning them into a bounded number of random-like bipartite graphs, enabling the analysis of complex structures and large datasets. Its applications include proving results in extremal graph theory, such as Szemeredi's theorem on arithmetic progressions, and simplifying property testing algorithms by reducing problems on dense graphs to manageable subgraphs. In contrast, the Removal Lemma helps detect and eliminate small forbidden subgraphs but relies extensively on the Regularity Lemma to establish key results in combinatorics and theoretical computer science.
Interconnections and Dependencies
The Removal lemma and Regularity lemma are deeply interconnected through their shared foundation in graph theory and combinatorics, where the Regularity lemma enables the decomposition of large graphs into structured partitions that facilitate property testing. The Removal lemma depends on this structural partitioning by leveraging the Regularity lemma's framework to prove that if a graph contains few copies of a forbidden subgraph, then a small number of edge removals can eliminate all such copies. This dependency highlights how the Regularity lemma provides the essential combinatorial scaffolding that underpins the quantitative bounds and applications of the Removal lemma in extremal graph theory and property testing.
Limitations and Challenges
The Removal Lemma faces limitations in its applicability to dense structures but struggles with providing quantitative bounds for sparse graphs, often leading to weak or non-constructive guarantees. The Regularity Lemma, while powerful for approximating large graphs through partitions, poses significant challenges due to its tower-type bound complexity and inefficiency in practical computations. Both lemmas encounter difficulties in extending their results to hypergraphs and other complex combinatorial settings, restricting their utility in broader algorithmic and combinatorial applications.
Future Directions and Open Problems
Exploring future directions for the Removal Lemma involves refining quantitative bounds and extending applications to sparse and hypergraph settings, which remain challenging due to combinatorial complexities. The Regularity Lemma's open problems include developing algorithmic versions with improved efficiency and extending its scope to infinite structures and higher-order combinatorics. Advancements in both lemmas will deepen understanding of graph limits, property testing, and additive combinatorics, driving progress in theoretical computer science and discrete mathematics.
Removal lemma Infographic
 libterm.com
libterm.com