Endomorphism is a mathematical concept where a function maps a structure to itself, preserving its operations and properties. This concept is fundamental in fields such as algebra and linear transformations, offering insight into internal symmetries and structural behaviors. Explore the rest of the article to deepen your understanding of endomorphisms and their applications.
Table of Comparison
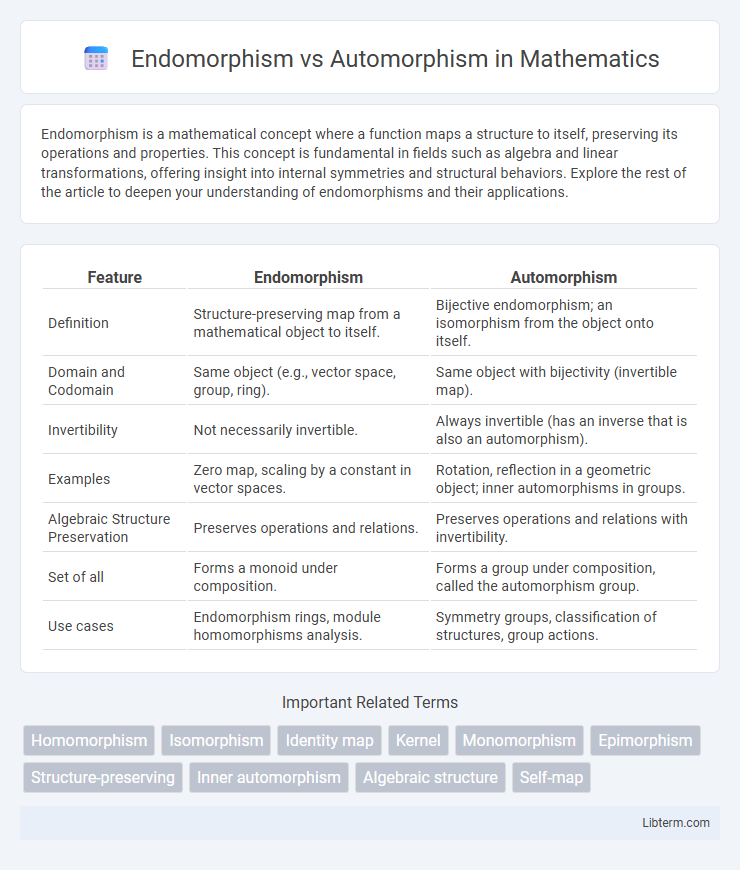
| Feature | Endomorphism | Automorphism |
|---|---|---|
| Definition | Structure-preserving map from a mathematical object to itself. | Bijective endomorphism; an isomorphism from the object onto itself. |
| Domain and Codomain | Same object (e.g., vector space, group, ring). | Same object with bijectivity (invertible map). |
| Invertibility | Not necessarily invertible. | Always invertible (has an inverse that is also an automorphism). |
| Examples | Zero map, scaling by a constant in vector spaces. | Rotation, reflection in a geometric object; inner automorphisms in groups. |
| Algebraic Structure Preservation | Preserves operations and relations. | Preserves operations and relations with invertibility. |
| Set of all | Forms a monoid under composition. | Forms a group under composition, called the automorphism group. |
| Use cases | Endomorphism rings, module homomorphisms analysis. | Symmetry groups, classification of structures, group actions. |
Introduction to Morphisms in Mathematics
Morphisms in mathematics represent structure-preserving maps between algebraic objects, with endomorphisms as morphisms from an object to itself, highlighting internal symmetries. Automorphisms are special endomorphisms that are bijective, serving as isomorphisms within a single structure to reveal its intrinsic invertibility and symmetries. Understanding the distinction between endomorphisms and automorphisms is crucial for studying algebraic structures like groups, rings, and vector spaces from a morphism-based perspective.
Defining Endomorphism: Concepts and Examples
Endomorphism is a function from a mathematical structure to itself that preserves the operations defining that structure, such as addition or multiplication in algebraic systems. In group theory, an endomorphism of a group G is a homomorphism ph: G - G that respects the group operation, meaning ph(xy) = ph(x)ph(y) for all elements x, y in G. Examples include the identity map and the zero homomorphism in vector spaces, illustrating how endomorphisms serve as internal structure-preserving transformations.
Understanding Automorphism: Key Features and Illustrations
Automorphisms are structure-preserving maps from a mathematical object to itself that are both injective and surjective, ensuring an isomorphism between the object and its image. Key features include bijectivity, the preservation of operation(s) defining the structure, and the existence of an inverse mapping that is also an automorphism. Illustrations often involve examples such as group automorphisms, where the internal symmetry of groups is explored through mappings that maintain group operations and element orders.
Fundamental Differences: Endomorphism vs Automorphism
Endomorphisms are structure-preserving maps from a mathematical object to itself, allowing non-invertible transformations, while automorphisms are bijective endomorphisms with invertible mappings. The fundamental difference lies in automorphisms requiring an inverse function that also preserves the structure, making them isomorphisms within the same object. In algebraic contexts such as groups, rings, or vector spaces, automorphisms form a group under composition, whereas endomorphisms do not necessarily have this property.
Algebraic Structures and Their Morphisms
In algebraic structures, an endomorphism is a morphism from a structure to itself preserving the operations defined on that structure, such as groups, rings, or vector spaces. An automorphism is a bijective endomorphism that has an inverse morphism, ensuring the structure's properties are maintained under both the mapping and its inverse. The study of these morphisms reveals fundamental symmetries and invariants within algebraic systems.
Real-World Applications of Endomorphisms
Endomorphisms play a crucial role in coding theory by enabling error detection and correction algorithms through structure-preserving transformations within algebraic systems. In cryptography, endomorphisms optimize cryptographic protocols by facilitating efficient computations on elliptic curves, enhancing security and performance. Additionally, endomorphisms assist in computer graphics by enabling transformations and symmetry operations on objects without altering their intrinsic properties, thus improving rendering techniques.
Practical Uses of Automorphisms in Mathematics
Automorphisms serve as powerful tools in mathematics for identifying symmetries within algebraic structures such as groups, rings, and fields, facilitating classification and structural analysis. They enable the study of invariant properties under isomorphisms, which aids in solving equations and understanding geometric transformations. In practical applications, automorphisms assist in cryptography, error-correcting codes, and the design of symmetric algorithms by preserving structural integrity while allowing controlled manipulation.
Endomorphism and Automorphism in Group Theory
Endomorphisms in group theory are homomorphisms from a group to itself that preserve the group operation but are not required to be bijective. Automorphisms are bijective endomorphisms, forming the automorphism group of a given group, which captures its symmetry structure. The study of endomorphisms and automorphisms provides crucial insights into group structure, invariants, and classification problems.
Importance in Cryptography and Computer Science
Endomorphisms and automorphisms play crucial roles in cryptography and computer science, particularly in the design of secure communication protocols and symmetric key algorithms. Endomorphisms, as structure-preserving maps within algebraic systems, enable efficient computation in elliptic curve cryptography by optimizing scalar multiplication. Automorphisms, being bijective endomorphisms, ensure structural invariance crucial for group theory applications, error-correcting codes, and cryptographic primitives, enhancing algorithmic stability and security.
Summary: Choosing Between Endomorphism and Automorphism
Endomorphisms are structure-preserving maps from an object to itself, applied broadly in algebra and linear transformations, while automorphisms are bijective endomorphisms that establish an isomorphism of an object with itself. Choosing between an endomorphism and an automorphism depends on whether invertibility is required; automorphisms guarantee reversible transformations, crucial in symmetry and group theory. Endomorphisms suit scenarios involving self-maps without the need for inverses, such as projection operators or transformations within algebraic structures.
Endomorphism Infographic
 libterm.com
libterm.com