A nowhere dense set is a concept in topology describing a set whose closure has an empty interior, meaning it is "thin" or sparse within the space it inhabits. These sets are important in understanding the structure of spaces and play a crucial role in areas such as real analysis and descriptive set theory. Discover how nowhere dense sets impact mathematical theory and why your understanding of them matters by reading the rest of this article.
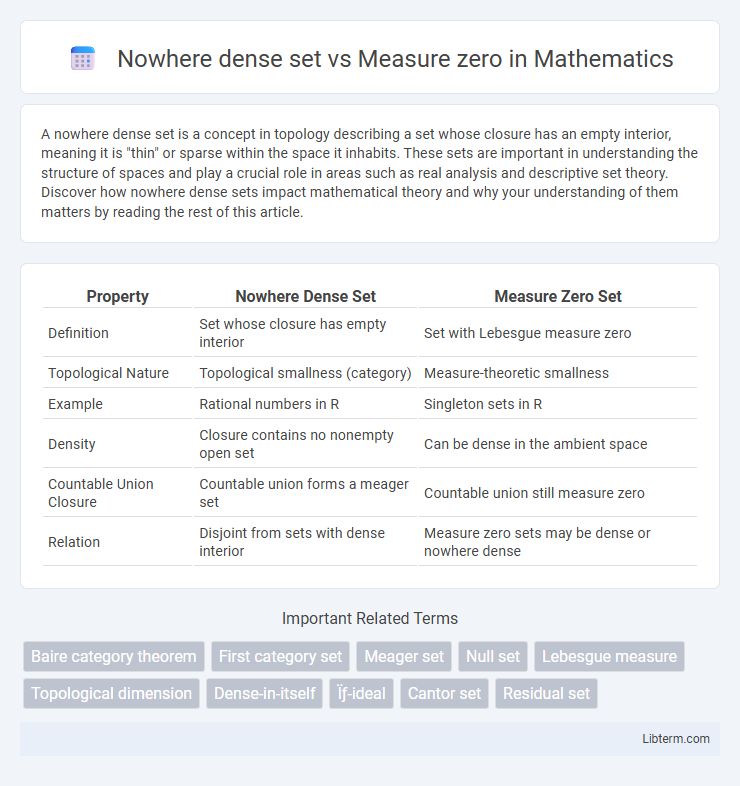
Table of Comparison
| Property | Nowhere Dense Set | Measure Zero Set |
|---|---|---|
| Definition | Set whose closure has empty interior | Set with Lebesgue measure zero |
| Topological Nature | Topological smallness (category) | Measure-theoretic smallness |
| Example | Rational numbers in R | Singleton sets in R |
| Density | Closure contains no nonempty open set | Can be dense in the ambient space |
| Countable Union Closure | Countable union forms a meager set | Countable union still measure zero |
| Relation | Disjoint from sets with dense interior | Measure zero sets may be dense or nowhere dense |
Introduction to Nowhere Dense Sets and Measure Zero
Nowhere dense sets are subsets of a topological space whose closure has empty interior, meaning they do not contain any open sets and are "thinly" distributed within the space. Measure zero sets, often studied in real analysis, are subsets of Euclidean space that can be covered by countably many intervals or balls with arbitrarily small total volume, indicating they occupy no "bulk" in terms of Lebesgue measure. Understanding the distinction between nowhere dense sets and measure zero sets is fundamental in real analysis, fractal geometry, and descriptive set theory, as these concepts describe different notions of smallness or thinness in mathematical spaces.
Defining Nowhere Dense Sets
Nowhere dense sets are defined as subsets of a topological space whose closure has an empty interior, meaning they contain no open subsets within their closure. These sets contrast with measure zero sets, which pertain to the Lebesgue measure and represent sets that occupy no volume in the real line or higher-dimensional spaces. While nowhere dense sets emphasize topological properties, measure zero sets focus on size in terms of measure theory.
Understanding Measure Zero Sets
Measure zero sets are subsets of a given space whose total length, area, or volume can be made arbitrarily small, meaning they occupy no "volume" in the sense of Lebesgue measure. These sets are critical in real analysis because they include countable sets, such as rational numbers, and certain fractals, demonstrating that having zero measure does not imply being negligible in topology. Understanding measure zero sets helps in differentiating between sets that are "small" in measure but can be topologically large, contrasting with nowhere dense sets that are topologically small but may have positive measure.
Key Differences Between Nowhere Dense and Measure Zero
Nowhere dense sets are those whose closure has empty interior, meaning they are "small" in a topological sense by lacking any non-empty open subsets. Measure zero sets have Lebesgue measure zero, indicating they occupy no volume or length in the measure-theoretic sense. Key differences include that nowhere dense sets can have positive measure, while measure zero sets can be dense in an interval, highlighting the distinct foundations of topological smallness versus measure-theoretic smallness.
Examples of Nowhere Dense Sets
A classic example of a nowhere dense set is the Cantor set, which is uncountable yet has empty interior and no intervals. Another example includes finite or countable sets like the rationals within real numbers, which are nowhere dense but do not occupy any real measure. Unlike measure zero sets, such as single points or lines in the plane, nowhere dense sets are defined by their topological property of containing no open subsets rather than their size in terms of Lebesgue measure.
Examples of Measure Zero Sets
The Cantor set exemplifies a classic measure zero set, containing uncountably many points yet occupying no length on the real line. Countable sets such as the rational numbers also have measure zero despite being dense in the real numbers. These sets contrast with nowhere dense sets, which lack any interval of positive length but do not necessarily have measure zero.
Topological vs Measure-Theoretic Perspectives
A nowhere dense set in topology is characterized by its closure having an empty interior, implying it is "small" in the sense of lacking any open subsets, whereas a measure zero set in measure theory possesses zero Lebesgue measure, indicating it occupies no volume in terms of size. From a topological perspective, nowhere dense sets are crucial in understanding the structure of spaces, particularly in Baire category theory, while measure zero sets are fundamental in quantifying size and integrability in analysis. These concepts intersect but differ significantly: nowhere dense sets may have positive measure, and measure zero sets can be dense, highlighting the distinct nature of "smallness" in topology versus measure theory.
Relationship Between Nowhere Density and Measure Zero
Nowhere dense sets have empty interior and are sparse in topological sense, while measure zero sets are negligible in terms of Lebesgue measure, meaning their total length, area, or volume is zero. Every nowhere dense set in \(\mathbb{R}^n\) can have positive measure, but every measure zero set is always nowhere dense in some contexts, specifically in perfect subsets where the measure zero set lacks interior points. The relationship highlights that nowhere density captures topological smallness, whereas measure zero captures metric smallness, and these properties can coincide or differ depending on the ambient space and set structure.
Applications in Analysis and Topology
Nowhere dense sets and measure zero sets play distinct roles in analysis and topology, with nowhere dense sets primarily characterizing "small" sets in a topological sense, such as in Baire category theory, where they help describe residual sets and generic properties. Measure zero sets are crucial in measure theory and Lebesgue integration, identifying sets negligible for integration and probability, impacting differentiation and function spaces. Their differing notions of smallness enable refined analysis in functional analysis, ergodic theory, and descriptive set theory, where the interplay between category and measure informs convergence, regularity, and structural properties of function and metric spaces.
Summary and Further Reading
A nowhere dense set in a topological space is a set whose closure has empty interior, meaning it is "small" in terms of topology but may still have positive measure. A measure zero set, often studied in measure theory, refers to sets that can be covered by intervals of arbitrarily small total length, indicating "smallness" from a measure perspective but not necessarily topological thinness. For deeper insights, explore works on Lebesgue measure, Baire category theorem, and their roles in real analysis and descriptive set theory.
Nowhere dense set Infographic
 libterm.com
libterm.com