Outer measure is a fundamental concept in measure theory used to assign a size or length to sets in a way that extends the notion of intervals in real numbers. It helps in defining measurable sets and is essential for understanding Lebesgue measure and integration. Explore the rest of the article to deepen your understanding of how outer measure underpins modern mathematical analysis.
Table of Comparison
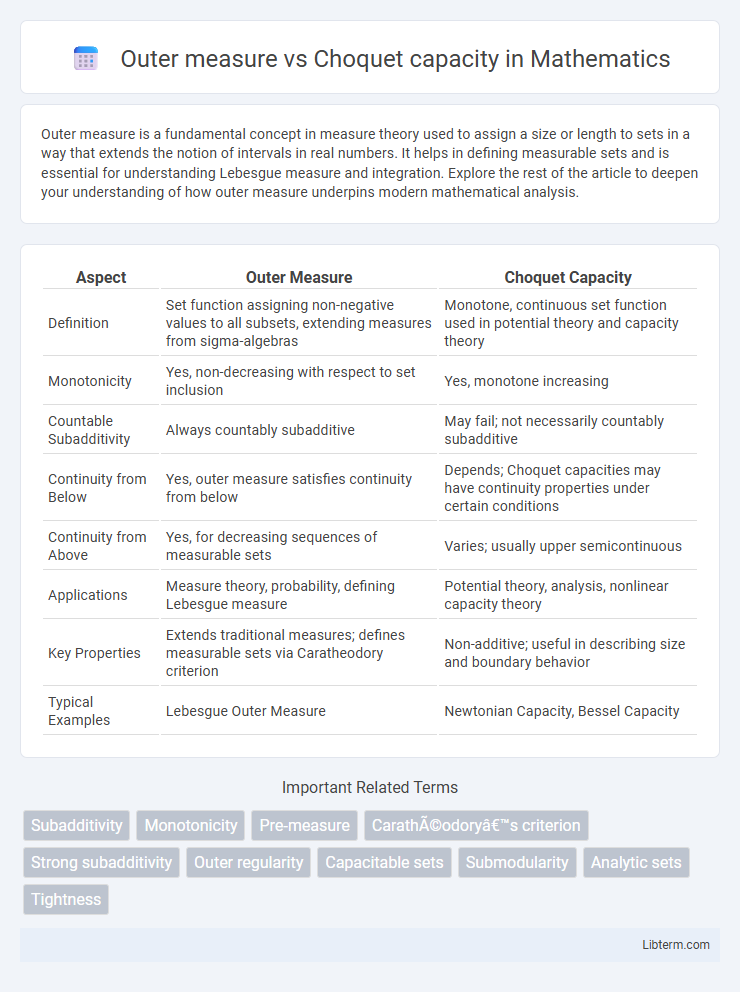
| Aspect | Outer Measure | Choquet Capacity |
|---|---|---|
| Definition | Set function assigning non-negative values to all subsets, extending measures from sigma-algebras | Monotone, continuous set function used in potential theory and capacity theory |
| Monotonicity | Yes, non-decreasing with respect to set inclusion | Yes, monotone increasing |
| Countable Subadditivity | Always countably subadditive | May fail; not necessarily countably subadditive |
| Continuity from Below | Yes, outer measure satisfies continuity from below | Depends; Choquet capacities may have continuity properties under certain conditions |
| Continuity from Above | Yes, for decreasing sequences of measurable sets | Varies; usually upper semicontinuous |
| Applications | Measure theory, probability, defining Lebesgue measure | Potential theory, analysis, nonlinear capacity theory |
| Key Properties | Extends traditional measures; defines measurable sets via Caratheodory criterion | Non-additive; useful in describing size and boundary behavior |
| Typical Examples | Lebesgue Outer Measure | Newtonian Capacity, Bessel Capacity |
Introduction to Outer Measure and Choquet Capacity
Outer measure provides a fundamental tool in measure theory, defining a set function that is countably subadditive, monotone, and assigns zero measure to the empty set, serving as a preliminary step towards defining complete measures. Choquet capacity generalizes this concept by introducing a set function that is monotone, continuous from below, and satisfies submodularity, enabling nuanced analysis in potential theory and applications involving non-additive measures. Both frameworks extend classical measure concepts, with outer measures laying the groundwork for measurable sets and Choquet capacities offering flexibility in capturing capacities beyond traditional measures.
Fundamental Concepts and Definitions
Outer measure is a set function that assigns a non-negative extended real number to all subsets of a given space, satisfying monotonicity and countable subadditivity, serving as a foundational tool in measure theory for extending measures to more general sets. Choquet capacity, a more general concept, is a set function fulfilling monotonicity and continuity properties, used in potential theory and decision theory to capture notions of "size" or "capacity" beyond measures, often defined via suprema over certain classes of measures. The fundamental difference lies in outer measures being countably subadditive set functions tailored for measure extension, whereas Choquet capacities relax additivity to encompass a broader class of set functions that quantify capacity with applications in nonlinear analysis.
Historical Background and Development
Outer measure originated from the early 20th-century work of Henri Lebesgue, who developed it to extend the concept of length to more complex sets, forming a foundational tool in measure theory and real analysis. Choquet capacity, introduced by Gustave Choquet in the 1950s, evolved as a nonlinear set function capturing potential theory and decision-making processes, emphasizing subadditivity and monotonicity properties. The development of Choquet capacity marked a significant advancement in functional analysis, broadening the scope of measure theory beyond additive measures and linking topology with probability and optimization theories.
Mathematical Formulation of Outer Measure
Outer measure is a function defined on all subsets of a given set, typically satisfying countable subadditivity, monotonicity, and null empty set properties, often constructed via an infimum of covers by measurable sets. Its mathematical formulation involves assigning to each subset the infimum of sums of measures over countable collections of covering sets, ensuring extensibility beyond sigma-algebras. In contrast, Choquet capacity generalizes outer measures by relaxing additivity requirements and emphasizing monotone set functions that allow for non-additive integration theories.
Mathematical Definition of Choquet Capacity
The Choquet capacity is a set function \( v: 2^X \to [0, \infty] \) defined on a set \( X \) that is monotone and continuous from below, satisfying \( v(\emptyset) = 0 \). Unlike an outer measure, the Choquet capacity need not be countably subadditive but must fulfill the property of monotonicity: if \( A \subseteq B \), then \( v(A) \leq v(B) \). This mathematical definition allows the Choquet capacity to generalize outer measures by relaxing subadditivity while still supporting important applications in potential theory and decision theory.
Key Differences Between Outer Measure and Choquet Capacity
Outer measure defines a set function that assigns a non-negative extended real number to all subsets of a space, primarily focusing on countable subadditivity and the measure of arbitrary sets. Choquet capacity, on the other hand, is a set function characterized by monotonicity and continuity from above or below, often used to generalize measures in potential theory. The key difference lies in outer measure's emphasis on sigma-subadditivity for measure extension versus Choquet capacity's flexible axiomatic framework accommodating nonlinear capacities and non-additive set functions.
Applications in Measure Theory and Potential Theory
Outer measure provides a foundational tool for constructing measures by assigning sizes to arbitrary subsets, crucial in defining Lebesgue measure and proving measurability. Choquet capacity extends this concept by capturing nonlinear set functions, instrumental in potential theory to analyze fine properties of functions, such as subharmonicity and balayage. Applications include solving Dirichlet problems, characterizing exceptional sets, and refining measure-theoretic approaches to capacity in fractal and irregular domains.
Properties and Examples of Outer Measures
Outer measures are set functions defined on all subsets of a given space that are non-negative, monotone, and countably subadditive, commonly used to extend measures beyond sigma-algebras. Key properties include null empty set, monotonicity (if A B then outer measure of A <= outer measure of B), and countable subadditivity (outer measure of a countable union <= sum of outer measures). Examples of outer measures include the Lebesgue outer measure on R, which assigns lengths to all subsets by infimum of coverings by intervals, contrasting with Choquet capacities that relax additivity in favor of monotonicity and continuity from below.
Properties and Examples of Choquet Capacities
Choquet capacities are set functions characterized by monotonicity, continuity from below, and submodularity, unlike outer measures that are countably subadditive and measure non-negative sets. Examples of Choquet capacities include the Lebesgue outer measure restricted to compact sets and the Hausdorff capacity, both highlighting their use in potential theory and fractal geometry. These capacities provide flexibility by allowing non-additive measures, useful for modeling uncertainty and irregular structures in mathematical analysis.
Conclusion: Comparative Insights and Future Perspectives
Outer measure provides a foundational, sigma-subadditive set function crucial for measure theory, whereas Choquet capacity extends these concepts by incorporating non-additive set functions that capture broader types of uncertainty and potential theory applications. Comparative insights reveal that Choquet capacities offer enhanced flexibility in modeling imprecise probabilities and risk, making them instrumental in decision theory and economics where classical outer measures may fall short. Future perspectives involve advancing computational methods for Choquet integrals and expanding applications in machine learning, finance, and environmental risk assessment, leveraging their ability to handle vagueness and interdependence beyond traditional measures.
Outer measure Infographic
 libterm.com
libterm.com