Fixed points are values in a function where the output equals the input, meaning f(x) = x. These points are critical in various fields like mathematics, computer science, and economics for analyzing system stability and behavior. Explore the rest of the article to understand how fixed points influence complex systems and practical applications.
Table of Comparison
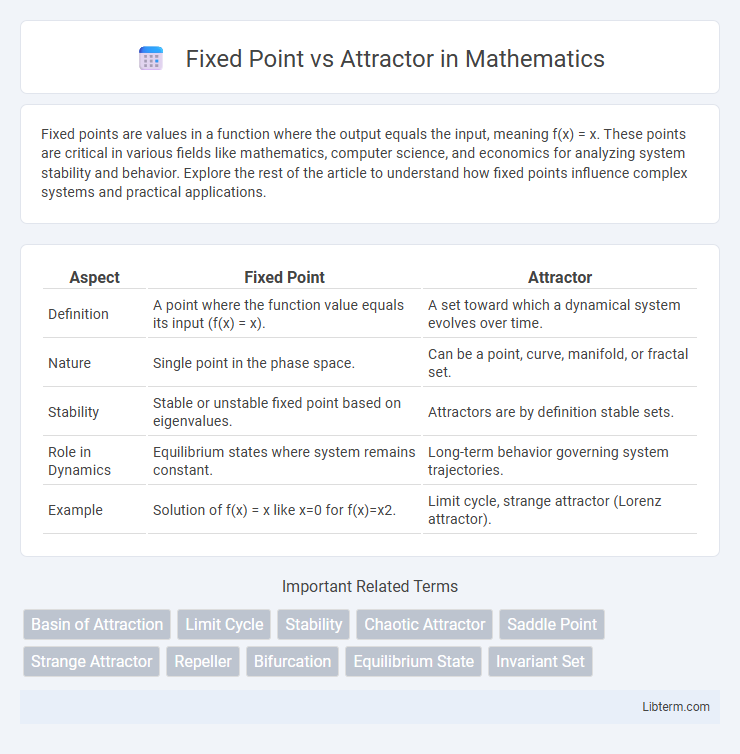
| Aspect | Fixed Point | Attractor |
|---|---|---|
| Definition | A point where the function value equals its input (f(x) = x). | A set toward which a dynamical system evolves over time. |
| Nature | Single point in the phase space. | Can be a point, curve, manifold, or fractal set. |
| Stability | Stable or unstable fixed point based on eigenvalues. | Attractors are by definition stable sets. |
| Role in Dynamics | Equilibrium states where system remains constant. | Long-term behavior governing system trajectories. |
| Example | Solution of f(x) = x like x=0 for f(x)=x2. | Limit cycle, strange attractor (Lorenz attractor). |
Introduction to Fixed Points and Attractors
Fixed points are states in a dynamical system where the system remains constant over time, representing equilibrium solutions where no change occurs. Attractors are sets towards which the system evolves from a variety of initial conditions, encompassing fixed points, limit cycles, or strange attractors in chaotic systems. Understanding fixed points and attractors is crucial for analyzing system stability, long-term behavior, and predicting outcomes in nonlinear dynamics.
Defining Fixed Points in Dynamical Systems
Fixed points in dynamical systems are specific states where the system remains unchanged over time, meaning the derivative or update function equals zero. They serve as critical anchors in the phase space, providing insight into system stability and long-term behavior. Understanding fixed points is essential for analyzing equilibrium conditions and predicting the evolution of nonlinear dynamic models.
Understanding Attractors: Types and Examples
Attractors in dynamical systems represent states or sets toward which a system evolves over time, with fixed points being a specific type of attractor where the system remains static. Common types of attractors include fixed point attractors, limit cycles, and strange attractors, each characterized by unique stability and behavior patterns. For example, a fixed point attractor corresponds to equilibrium in physical processes, while strange attractors describe chaotic systems with fractal structures, such as the Lorenz attractor in weather models.
Key Differences Between Fixed Points and Attractors
Fixed points are specific states where a system remains constant over time, while attractors represent sets or regions toward which systems evolve. Fixed points can be stable or unstable, acting as equilibrium points, whereas attractors encompass fixed points, limit cycles, or chaotic sets that shape long-term behavior. The key difference lies in attractors guiding trajectories in phase space, whereas fixed points denote precise invariant states.
Mathematical Representation and Notation
A fixed point in mathematics is a point \( x^* \) such that \( f(x^*) = x^* \) for a given function \( f \), representing an invariant under the function's mapping. An attractor, often denoted as \( A \), is a set toward which a dynamical system evolves over time, satisfying \( \lim_{n \to \infty} f^n(x) = A \) for \( x \) in some neighborhood of \( A \). While every attractor may contain fixed points, fixed points themselves are described by the simple equation \( f(x^*) = x^* \), whereas attractors encompass a broader class including fixed points, limit cycles, and strange attractors, often characterized via invariant sets and stability conditions in the phase space.
Stability Analysis: Fixed Points vs Attractors
Fixed points describe specific states where a dynamical system remains unchanged, while attractors represent sets or regions toward which nearby states evolve over time. Stability analysis examines eigenvalues or Lyapunov exponents at fixed points to determine if small perturbations decay, indicating stability, whereas attractors are characterized by their basin of attraction, defining the initial conditions that converge to them. Understanding the distinction aids in predicting long-term behavior, where stable fixed points are simple attractors and more complex attractors include limit cycles and strange attractors in nonlinear systems.
Applications in Real-World Systems
Fixed points serve as equilibrium states where system variables remain constant, crucial in engineering systems for stability analysis and control design. Attractors represent long-term behavior patterns in dynamical systems, essential in climate modeling, neuroscience, and economics to predict system evolution and chaotic behavior. Understanding the distinction enhances the modeling of physical processes, enabling precise control in robotics and forecasting in meteorology.
Visualizing Behavior: Phase Space and Trajectories
Fixed points represent states in phase space where trajectories converge and system variables remain constant over time, acting as equilibrium points. Attractors extend this concept by encompassing sets or regions toward which trajectories evolve, potentially forming limit cycles or strange attractors in nonlinear dynamics. Visualizing these behaviors in phase space reveals how system trajectories converge, spiral, or oscillate around fixed points and attractors, providing insight into system stability and long-term dynamics.
Common Misconceptions and Clarifications
Fixed points and attractors are often conflated, but fixed points are specific states where the system remains unchanged, while attractors can be more complex sets like limit cycles or strange attractors that systems approach over time. A common misconception is that all attractors are fixed points; however, attractors encompass any stable long-term behavior, including periodic or chaotic patterns. Clarifying this distinction is crucial for accurately analyzing dynamical systems and understanding their stability properties.
Conclusion: Choosing Between Fixed Points and Attractors
Choosing between fixed points and attractors depends on the stability and complexity of the system's behavior. Fixed points represent static equilibrium states with no movement, ideal for simple, predictable systems requiring steady-state solutions. Attractors characterize dynamic long-term behaviors in nonlinear systems, offering insights into complex, oscillatory, or chaotic phenomena for advanced modeling and analysis.
Fixed Point Infographic
 libterm.com
libterm.com