The dot product calculates the scalar result from multiplying two vectors, capturing their directional relationship and magnitude similarity. This operation is fundamental in fields like physics and computer graphics to determine angles, projections, and work done by forces. Explore the rest of the article to deepen your understanding of the dot product and its powerful applications.
Table of Comparison
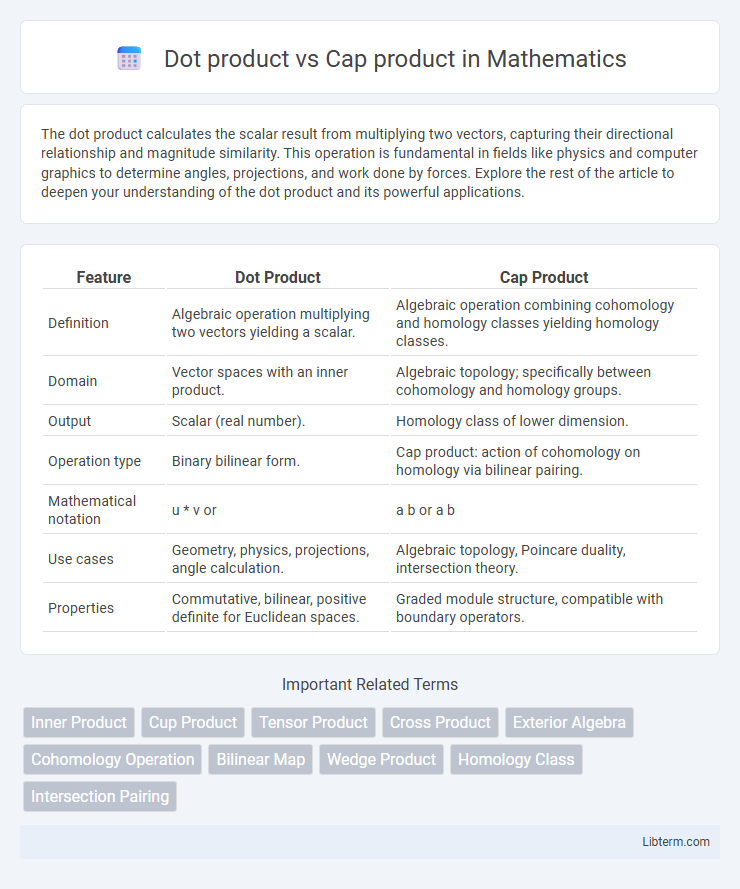
| Feature | Dot Product | Cap Product |
|---|---|---|
| Definition | Algebraic operation multiplying two vectors yielding a scalar. | Algebraic operation combining cohomology and homology classes yielding homology classes. |
| Domain | Vector spaces with an inner product. | Algebraic topology; specifically between cohomology and homology groups. |
| Output | Scalar (real number). | Homology class of lower dimension. |
| Operation type | Binary bilinear form. | Cap product: action of cohomology on homology via bilinear pairing. |
| Mathematical notation | u * v or |
a b or a b |
| Use cases | Geometry, physics, projections, angle calculation. | Algebraic topology, Poincare duality, intersection theory. |
| Properties | Commutative, bilinear, positive definite for Euclidean spaces. | Graded module structure, compatible with boundary operators. |
Introduction to Dot Product and Cap Product
The dot product is a scalar value obtained by multiplying corresponding components of two vectors and summing the results, fundamental in measuring vector magnitude and angle. The cap product, an operation in algebraic topology, combines cohomology classes with homology classes, producing lower-dimensional homology classes. Understanding the dot product aids in vector projection and orthogonality, while the cap product plays a key role in relating cohomological and homological structures within topological spaces.
Fundamental Concepts: Vectors and Operations
The dot product is a scalar operation that multiplies two vectors by summing the products of their corresponding components, measuring the magnitude of one vector projected onto another. The cap product, also known as the cup product in algebraic topology, combines cohomology and homology classes, capturing intricate topological information in a graded algebraic structure. Understanding the dot product's role in Euclidean geometry contrasts with the cap product's function in algebraic topology, highlighting different applications of vector and multilinear operations.
Mathematical Definition of Dot Product
The dot product is a binary operation that takes two equal-length sequences of numbers (usually vectors) and returns a single scalar, calculated as the sum of the products of corresponding entries. Formally, for vectors a = (a1, a2, ..., an) and b = (b1, b2, ..., bn), the dot product is defined as a * b = (aibi) for i = 1 to n. This differs from the cap product in algebraic topology, where the cap product operates between cohomology and homology classes to yield lower-dimensional homology classes, emphasizing its role in topological structures rather than pure vector algebra.
Mathematical Definition of Cap Product
The cap product is a bilinear operation defined between a cohomology class and a homology class, resulting in a lower-dimensional homology class, typically denoted as \( \frown: H^p(X; R) \times H_q(X; R) \rightarrow H_{q-p}(X; R) \). It encodes the action of cochains on chains by capping a cohomology class with a homology class, thus providing a way to "cap off" dimensions and form intersections in algebraic topology. Unlike the dot product, which is an inner product on vectors in a Euclidean space, the cap product operates in the setting of singular homology and cohomology, capturing topological invariants related to orientation and duality.
Geometric Interpretation: Dot Product vs Cap Product
The dot product measures the projection of one vector onto another, yielding a scalar that indicates the magnitude of their alignment and cosine of the angle between them. The cap product operates within algebraic topology, combining a cohomology class with a homology class to produce a lower-dimensional homology class, reflecting intersection properties within topological spaces. Geometrically, the dot product quantifies vector alignment in Euclidean space, while the cap product interprets interactions between algebraic invariants and geometric cycles.
Key Differences: Dot Product and Cap Product
The dot product is an algebraic operation that takes two vectors and returns a scalar, commonly used to measure the angle between vectors or project one vector onto another. In contrast, the cap product is a topological operation in algebraic topology that combines a cohomology class with a homology class to produce a lower-dimensional homology class, facilitating the interaction between homology and cohomology groups. Key differences lie in their domains and outputs: the dot product belongs to vector algebra yielding scalar values, while the cap product operates within homological algebra producing homology classes.
Applications in Mathematics and Physics
The dot product is crucial in physics for calculating work, projection, and understanding vector relationships like angles and magnitudes. In mathematics, it aids in defining orthogonality in inner product spaces and simplifying vector algebra operations. The cap product, used primarily in algebraic topology, enables interaction between homology and cohomology classes, facilitating computations in manifold theory and the classification of topological spaces.
Computational Examples and Calculations
The dot product, computed as the sum of the products of corresponding vector components, results in a scalar value often used to determine angles or projections between vectors, such as calculating \( \mathbf{a} \cdot \mathbf{b} = a_1b_1 + a_2b_2 + a_3b_3 \). The cap product, in algebraic topology, combines a cohomology class and a homology class to produce another homology class, typically represented through chain and cochain interactions, for example, \( \alpha \frown \sigma \) where \( \alpha \) is a cochain and \( \sigma \) a chain, with computations involving boundary operators and evaluation maps. Computationally, the dot product is straightforward in Euclidean space with vector components, while the cap product requires more abstract algebraic structures like simplicial complexes, making its calculations dependent on the underlying topological space and chain complex definitions.
Common Mistakes and Misconceptions
Confusing the dot product with the cap product often arises from misunderstanding their distinct mathematical contexts: the dot product is an algebraic operation on vectors yielding a scalar, while the cap product operates in algebraic topology between cohomology and homology classes, producing lower-dimensional homology classes. A common mistake is treating the cap product as a simple vector operation, ignoring its role in relating chain complexes and cochain complexes. Misconceptions also include assuming commutativity or similar computational properties for both products, despite the cap product's dependence on orientation and boundary conditions.
Conclusion: Choosing the Right Product
The dot product measures the scalar projection between two vectors, making it ideal for applications requiring magnitude and directional correlation such as physics and computer graphics. The cap product, used in algebraic topology, combines cohomology and homology classes to provide insights into space structure and duality. Selecting the appropriate product depends on whether the problem involves vector magnitude interactions or topological space analysis.
Dot product Infographic
 libterm.com
libterm.com