Functional design focuses on practicality, ensuring that every element serves a clear purpose to enhance usability and efficiency. This approach prioritizes user experience by simplifying interactions and eliminating unnecessary complexity. Explore the rest of this article to discover how functional design can transform your everyday products and spaces.
Table of Comparison
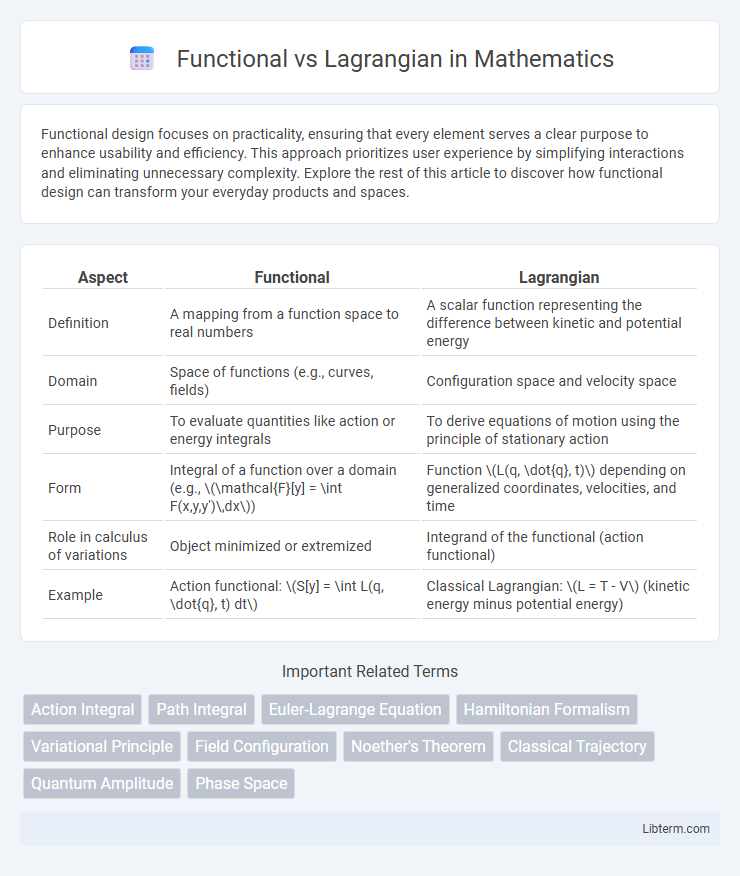
| Aspect | Functional | Lagrangian |
|---|---|---|
| Definition | A mapping from a function space to real numbers | A scalar function representing the difference between kinetic and potential energy |
| Domain | Space of functions (e.g., curves, fields) | Configuration space and velocity space |
| Purpose | To evaluate quantities like action or energy integrals | To derive equations of motion using the principle of stationary action |
| Form | Integral of a function over a domain (e.g., \(\mathcal{F}[y] = \int F(x,y,y')\,dx\)) | Function \(L(q, \dot{q}, t)\) depending on generalized coordinates, velocities, and time |
| Role in calculus of variations | Object minimized or extremized | Integrand of the functional (action functional) |
| Example | Action functional: \(S[y] = \int L(q, \dot{q}, t) dt\) | Classical Lagrangian: \(L = T - V\) (kinetic energy minus potential energy) |
Introduction to Functional and Lagrangian Approaches
Functional approaches in physics formulate problems by defining a functional, typically representing the total energy or action, which depends on fields or paths and their derivatives; optimizing this functional determines the system's behavior. The Lagrangian approach specifically expresses the dynamics through the Lagrangian function, the difference between kinetic and potential energy, allowing derivation of equations of motion via the principle of least action. Both frameworks provide powerful methods to analyze physical systems, with functional methods offering general optimization perspectives and the Lagrangian formalism central to classical mechanics and field theory.
Fundamental Definitions: Functional vs Lagrangian
A functional is a mapping from a space of functions to real numbers, often expressed as an integral involving the function and its derivatives, fundamental in variational calculus for finding extrema of functionals. The Lagrangian is a function that summarizes the dynamics of a system, typically defined as the difference between kinetic and potential energy in classical mechanics, used to formulate the equations of motion via the Euler-Lagrange equation. The key distinction lies in the functional being an integral operator acting on functions, while the Lagrangian is the integrand specifying the system's local behavior within that integral.
Historical Origins and Development
The historical origins of functional and Lagrangian mechanics trace back to the 18th century with Leonhard Euler and Joseph-Louis Lagrange, who formulated the principles that redefined classical mechanics. Functional analysis in mechanics evolved through the calculus of variations, enabling the characterization of physical systems via functionals representing action or energy. Lagrangian mechanics, rooted in the principle of least action, revolutionized dynamics by expressing equations of motion through scalar functions, significantly influencing subsequent developments in theoretical physics.
Mathematical Foundations and Formalism
Functional analysis underpins the study of infinite-dimensional vector spaces, emphasizing mappings between functions, while the Lagrangian formalism centers on the principle of stationary action to derive equations of motion in classical mechanics. The mathematical foundation of functional approaches involves Hilbert and Banach spaces, integral transforms, and operator theory, whereas the Lagrangian method utilizes calculus of variations, differential equations, and symplectic geometry. Both frameworks employ rigorous formalism to connect physical phenomena with abstract mathematical structures, enabling precise formulation and solution of dynamic systems.
Applications in Classical Mechanics
Functional approaches in classical mechanics primarily utilize the principle of least action, providing a powerful framework for deriving equations of motion through the calculus of variations. Lagrangian mechanics reformulates Newtonian mechanics by expressing dynamics in terms of kinetic and potential energy, enabling the analysis of complex systems with constraints and generalized coordinates. Applications span from rigid body dynamics and orbital mechanics to modern fields such as quantum mechanics and field theory, where these formulations offer elegant, coordinate-independent solutions.
Role in Quantum Field Theory
Functional methods in Quantum Field Theory (QFT) provide a framework for calculating path integrals, enabling the evaluation of correlation functions and generating functionals crucial for perturbative expansions. The Lagrangian formalism defines the dynamics of fields through an action principle, specifying the fundamental interactions and symmetries of the theory. Together, the functional approach translates the Lagrangian density into a generating functional, facilitating the computation of Green's functions and scattering amplitudes in QFT.
Comparative Advantages and Limitations
Functional methods excel in providing direct solutions to differential equations by minimizing energy or action, offering intuitive physical interpretations and efficiency in complex boundary conditions. Lagrangian approaches leverage variational principles to derive equations of motion, facilitating the incorporation of constraints and symmetries, but can lead to more complex mathematical formulations. Functional techniques often simplify numerical implementations, whereas Lagrangian methods provide greater flexibility in theoretical analysis and generalized coordinate systems.
Examples: Problems Illustrated with Both Methods
In fluid mechanics, both Functional and Lagrangian approaches are employed to analyze particle trajectories and flow behavior. The Functional method focuses on velocity fields as functions of spatial coordinates and time, allowing the study of steady and unsteady flow patterns, such as potential flow around airfoils or Poiseuille flow in pipes. The Lagrangian approach tracks individual fluid particles by solving ordinary differential equations for position over time, effectively illustrating problems like pollutant dispersion in rivers or the motion of droplets in multiphase flows.
Contemporary Research and Innovations
Contemporary research in fluid dynamics emphasizes the functional approach for its direct applicability in numerical simulations and real-time data analysis, leveraging function-based models to capture complex flow behaviors. Innovations in Lagrangian methods focus on particle tracking and pathline reconstruction, enhancing the accuracy of turbulence modeling and environmental fluid studies. Cutting-edge advancements integrate machine learning with both frameworks to optimize predictive capabilities and computational efficiency in complex fluid systems.
Conclusion: Choosing the Right Approach
Selecting between functional and Lagrangian methods depends on the specific problem context and desired outcomes in classical mechanics or field theory. Functional approaches excel in dealing with systems characterized by infinite degrees of freedom or when constraints are complex, while the Lagrangian method provides a more straightforward formulation for finite-dimensional systems with well-defined coordinate choices. Evaluating factors such as computational efficiency, ease of implementing constraints, and problem dimensionality guides the optimal decision for accurate modeling and solution derivation.
Functional Infographic
 libterm.com
libterm.com