Segmenting your audience allows you to tailor marketing strategies that directly address specific customer needs, boosting engagement and conversion rates. Understanding the distinct characteristics within each segment helps optimize resource allocation and enhances overall campaign effectiveness. Explore the rest of the article to learn how precise segmentation can transform Your business outcomes.
Table of Comparison
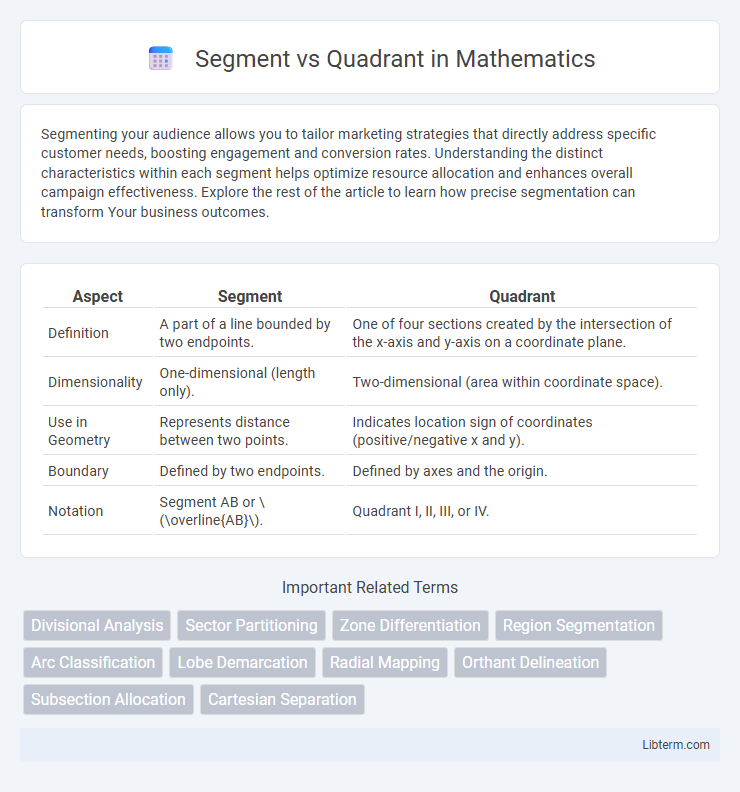
| Aspect | Segment | Quadrant |
|---|---|---|
| Definition | A part of a line bounded by two endpoints. | One of four sections created by the intersection of the x-axis and y-axis on a coordinate plane. |
| Dimensionality | One-dimensional (length only). | Two-dimensional (area within coordinate space). |
| Use in Geometry | Represents distance between two points. | Indicates location sign of coordinates (positive/negative x and y). |
| Boundary | Defined by two endpoints. | Defined by axes and the origin. |
| Notation | Segment AB or \(\overline{AB}\). | Quadrant I, II, III, or IV. |
Introduction to Segments and Quadrants
Segments represent portions of a circle defined by two radii and the enclosed arc, crucial in geometry for calculating areas and lengths. Quadrants divide a Cartesian plane into four equal parts, each representing 90-degree sections of a circle, essential in graphing and trigonometric analysis. Understanding both segments and quadrants enables precise interpretation of circular and coordinate-based problems in mathematics.
Defining Segments
Segments are portions of a circle defined by a chord and the corresponding arc, representing a specific area within the circle's boundary. Quadrants divide the circle into four equal parts using two perpendicular radii intersecting at the center, each quadrant covering 90 degrees. Understanding segments involves calculating areas constrained by curved boundaries, whereas quadrants focus on equal angular divisions.
Defining Quadrants
Quadrants are defined as four equal parts created by the intersection of two perpendicular axes, typically the x-axis and y-axis, dividing a plane into sections named as Quadrant I, II, III, and IV. Each quadrant represents a unique combination of positive and negative values on the Cartesian coordinate system, providing a framework for analyzing the sign and relationship of ordered pairs. In contrast to segments, which refer to portions of a curve or line, quadrants offer a spatial division essential for graphing functions and solving geometric problems.
Key Differences Between Segments and Quadrants
Segments are portions of a circle defined by a chord and the corresponding arc, representing a curved area bounded by a straight line and the curve, while quadrants are four equal parts created by two perpendicular radii dividing a circle into 90-degree sections. Segments vary in size depending on the chord length and arc, whereas quadrants are fixed at one-fourth of the circle's area, each spanning a right angle. Key differences include segments being irregular, curved-surface areas and quadrants being precise right-angle sectors with equal area portions of the circle.
Applications of Segments in Various Fields
Segments are extensively applied in fields such as marketing for customer segmentation, allowing businesses to target specific consumer groups based on behavior or demographics. In geometry and computer graphics, line segments help define shapes and paths, facilitating accurate modeling and rendering processes. Additionally, segments are used in data analysis to partition datasets for focused insights, improving decision-making across industries like finance and healthcare.
Applications of Quadrants in Analysis
Quadrants are essential in data analysis for categorizing variables into four distinct sections based on two axes, facilitating visual interpretation of relationships and patterns. Common applications include market segmentation, where quadrants help identify customer groups by behavior and value, and performance analysis, distinguishing areas of strengths and weaknesses in business metrics. This method enables precise targeting and strategic decision-making by simplifying complex data into actionable insights.
Advantages of Using Segments
Segments allow precise targeting by categorizing a market into distinct groups based on specific criteria such as demographics, behavior, or preferences. This granularity enables more effective marketing strategies and personalized communication, leading to higher customer engagement and conversion rates. Compared to quadrants, segments offer greater flexibility and adaptability in addressing diverse customer needs and optimizing resource allocation.
Benefits of Quadrant Analysis
Quadrant analysis offers distinct advantages by visually categorizing data into four clear segments based on two variables, enhancing interpretability and strategic decision-making. This method highlights relationships, trends, and outliers more effectively than simple segmentation, allowing businesses to prioritize resources and tailor strategies to specific market needs. The clarity and simplicity of quadrant analysis facilitate faster insights, making it invaluable for competitive analysis, customer segmentation, and performance evaluation.
Choosing Between Segments and Quadrants
Choosing between segments and quadrants depends on the analysis complexity and data categorization needs. Segments divide data into distinct groups based on specific criteria, ideal for targeted marketing and customer profiling. Quadrants split data along two variables into four parts, useful for visualizing relationships and prioritizing decision-making.
Conclusion: Segment vs Quadrant
Segments divide circles into distinct regions defined by two radii and the connecting arc, useful for precise area calculations within a curve. Quadrants partition a circle into four equal 90-degree sections, simplifying angle measurement and coordinate localization. Choosing between segment and quadrant depends on the specific geometric requirements, such as detailed arc analysis versus straightforward quarter-circle division.
Segment Infographic
 libterm.com
libterm.com