An abelian category is a fundamental concept in homological algebra and category theory, providing a framework where morphisms and objects behave similarly to those in the category of abelian groups. This structure allows for the definition of kernels, cokernels, exact sequences, and image factorizations, facilitating the study of complex algebraic objects and their relationships. Explore the rest of the article to understand how abelian categories underpin many modern mathematical theories and your work in abstract algebra.
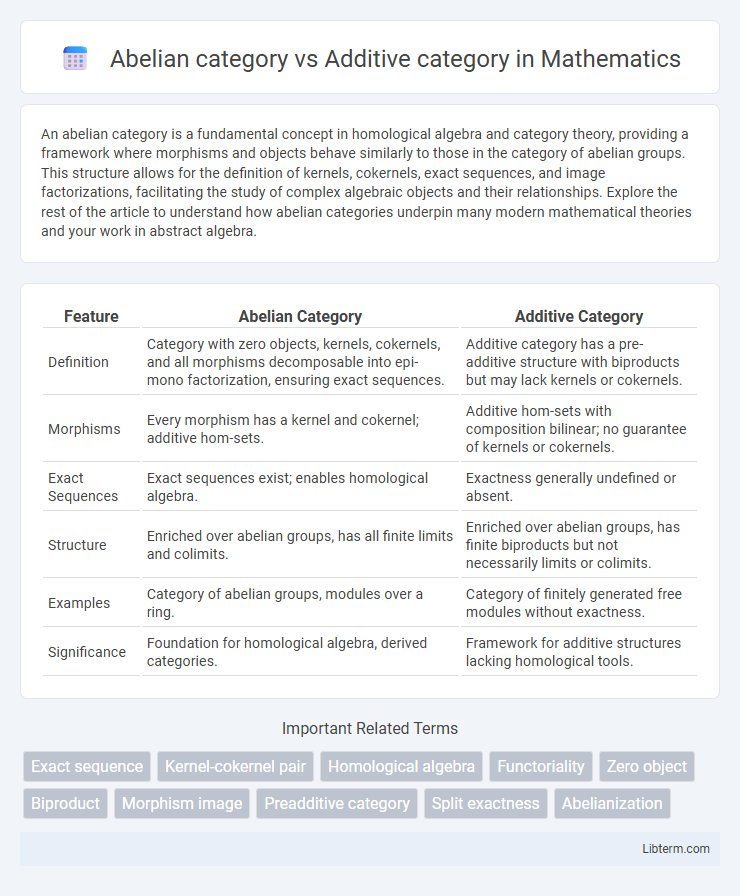
Table of Comparison
| Feature | Abelian Category | Additive Category |
|---|---|---|
| Definition | Category with zero objects, kernels, cokernels, and all morphisms decomposable into epi-mono factorization, ensuring exact sequences. | Additive category has a pre-additive structure with biproducts but may lack kernels or cokernels. |
| Morphisms | Every morphism has a kernel and cokernel; additive hom-sets. | Additive hom-sets with composition bilinear; no guarantee of kernels or cokernels. |
| Exact Sequences | Exact sequences exist; enables homological algebra. | Exactness generally undefined or absent. |
| Structure | Enriched over abelian groups, has all finite limits and colimits. | Enriched over abelian groups, has finite biproducts but not necessarily limits or colimits. |
| Examples | Category of abelian groups, modules over a ring. | Category of finitely generated free modules without exactness. |
| Significance | Foundation for homological algebra, derived categories. | Framework for additive structures lacking homological tools. |
Introduction to Abelian and Additive Categories
Additive categories are categories enriched over abelian groups where every hom-set is an abelian group and composition is bilinear, supporting finite biproducts that combine products and coproducts. Abelian categories extend additive categories by incorporating exact sequences, kernels, and cokernels, allowing a well-defined notion of exactness essential for homological algebra. These structures provide a rigorous framework for generalizing module theory and developing advanced concepts in algebraic geometry and representation theory.
Defining Additive Categories
Additive categories are defined as categories enriched over the category of abelian groups, where each hom-set is an abelian group and composition of morphisms is bilinear. These categories possess finite biproducts, allowing the direct sum of objects, which serves as both product and coproduct. Unlike Abelian categories that require kernels and cokernels with exact sequences, additive categories do not necessitate these exactness properties, making them a more general framework in homological algebra.
Key Properties of Additive Categories
Additive categories are enriched over abelian groups with a zero object, biproducts, and morphism sets forming abelian groups, enabling addition of morphisms and direct sum decomposition. Unlike abelian categories, additive categories do not require every morphism to have a kernel and cokernel or the existence of exact sequences. The key properties of additive categories include the existence of finite biproducts, additive structure on hom-sets, and the presence of a zero morphism that acts as an additive identity.
Understanding Abelian Categories
Abelian categories generalize the structure of modules over a ring, featuring kernels and cokernels with all morphisms allowing exact sequences that classify homological algebra. Unlike additive categories, which merely require biproducts and abelian group structures on Hom-sets, abelian categories ensure every monomorphism and epimorphism is a kernel or cokernel, facilitating a robust notion of exactness. This precise framework underpins key concepts in algebraic geometry, representation theory, and homological algebra by enabling systematic treatment of exact sequences and derived functors.
Essential Properties of Abelian Categories
Abelian categories extend additive categories by requiring all morphisms to have kernels and cokernels, ensuring every monomorphism and epimorphism is normal. They feature exact sequences enabling homological algebra and guarantee that every morphism factorizes through its image and coimage, making them ideal for studying exactness properties. These essential properties facilitate a rich algebraic structure that supports concepts like exact functors and derived categories.
Structural Differences: Abelian vs Additive
An Abelian category is an additive category with kernels and cokernels, ensuring every monomorphism and epimorphism is normal, which guarantees exact sequences and homological algebra applications. Additive categories only require the existence of finite biproducts and hom-sets with abelian group structures, lacking the guarantees of exactness and normality present in Abelian categories. The fundamental structural difference lies in Abelian categories possessing rich exactness properties that enable robust manipulation of morphisms, while additive categories provide a more minimal framework focused primarily on direct sums and additive morphism composition.
Morphisms in Additive and Abelian Categories
Morphisms in additive categories are homomorphisms between objects where morphism sets form abelian groups, enabling addition and zero morphisms. In abelian categories, every morphism has a kernel and cokernel, and all monomorphisms and epimorphisms are normal, ensuring exactness and the existence of well-defined images and coimages. This structure allows abelian categories to generalize module categories with richer morphism properties, crucial for homological algebra.
Examples of Additive and Abelian Categories
Additive categories include examples such as the category of abelian groups, the category of modules over a ring, and the category of vector spaces over a field, characterized by having finite biproducts and additive hom-sets. Abelian categories, which are a refined subclass of additive categories, include examples like the category of abelian groups, the category of finitely generated modules over a Noetherian ring, and the category of coherent sheaves on a scheme, distinguished by having kernels and cokernels, and every monomorphism and epimorphism being normal. These examples illustrate the structural richness of abelian categories compared to general additive categories, where exact sequences and homological methods are applicable.
Categorical Importance in Algebra
Abelian categories generalize module theory by ensuring exact sequences and kernels coincide, enabling a robust framework for homological algebra and derived functors. Additive categories provide the baseline structure with biproducts and hom-sets forming abelian groups but lack the full exactness properties needed for advanced algebraic constructs. The categorical importance lies in abelian categories' role in unifying various algebraic theories, such as sheaf cohomology and representation theory, through their enriched exactness and kernel-cokernel duality.
Summary: Choosing Abelian or Additive Categories
Abelian categories provide a comprehensive framework with kernels, cokernels, and exact sequences, making them ideal for homological algebra and module theory. Additive categories, equipped with finite biproducts and abelian group hom-sets, serve as a more general setting where exactness and kernel-cokernel pairs may not exist. Choosing between Abelian and additive categories depends on whether one requires full exactness and rich morphism structures (Abelian) or a simpler additive structure without full exactness (Additive).
Abelian category Infographic
 libterm.com
libterm.com