The bordism spectrum is a fundamental object in algebraic topology that encodes information about manifolds up to bordism equivalence. It plays a crucial role in the study of generalized homology theories and stable homotopy theory, providing tools for understanding manifold classifications. Explore the rest of the article to uncover how the bordism spectrum connects these deep mathematical concepts and benefits your research.
Table of Comparison
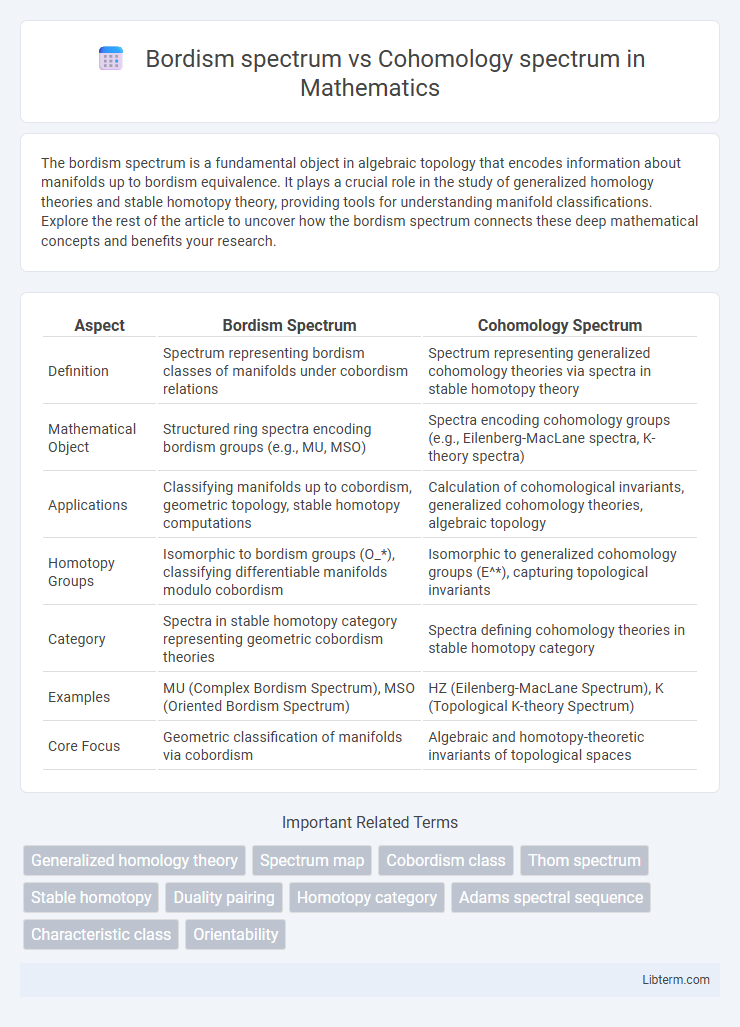
| Aspect | Bordism Spectrum | Cohomology Spectrum |
|---|---|---|
| Definition | Spectrum representing bordism classes of manifolds under cobordism relations | Spectrum representing generalized cohomology theories via spectra in stable homotopy theory |
| Mathematical Object | Structured ring spectra encoding bordism groups (e.g., MU, MSO) | Spectra encoding cohomology groups (e.g., Eilenberg-MacLane spectra, K-theory spectra) |
| Applications | Classifying manifolds up to cobordism, geometric topology, stable homotopy computations | Calculation of cohomological invariants, generalized cohomology theories, algebraic topology |
| Homotopy Groups | Isomorphic to bordism groups (O_*), classifying differentiable manifolds modulo cobordism | Isomorphic to generalized cohomology groups (E^*), capturing topological invariants |
| Category | Spectra in stable homotopy category representing geometric cobordism theories | Spectra defining cohomology theories in stable homotopy category |
| Examples | MU (Complex Bordism Spectrum), MSO (Oriented Bordism Spectrum) | HZ (Eilenberg-MacLane Spectrum), K (Topological K-theory Spectrum) |
| Core Focus | Geometric classification of manifolds via cobordism | Algebraic and homotopy-theoretic invariants of topological spaces |
Introduction to Bordism and Cohomology Spectra
Bordism spectra represent classes of manifolds under equivalence by bordism, encoding geometric information through stable homotopy theory and serving as foundational tools in algebraic topology. Cohomology spectra generalize cohomology theories by associating spectrum objects to cohomology functors, capturing algebraic invariants of spaces across dimensions. Both spectra unify geometric and algebraic perspectives, with bordism spectra focusing on manifold classifications and cohomology spectra providing generalized cohomological data.
Defining the Bordism Spectrum
The bordism spectrum is defined by representing cobordism classes of manifolds through stable homotopy theory, often constructed via Thom spectra associated with vector bundles over classifying spaces. This spectrum encodes geometric information about manifolds up to bordism equivalence and serves as a foundational object in stable homotopy category. In contrast, the cohomology spectrum captures generalized cohomology theories, focusing on algebraic invariants rather than geometric bordism relations.
Understanding the Cohomology Spectrum
The cohomology spectrum is a fundamental object in stable homotopy theory representing generalized cohomology theories through spectra, enabling algebraic invariants to classify topological spaces. Unlike the bordism spectrum, which encodes geometric information about manifolds and cobordism classes, the cohomology spectrum provides a framework for computing cohomological operations and stable homotopy groups. Its construction allows the translation of geometric problems into algebraic settings, making it essential for understanding complex relationships in algebraic topology.
Key Differences Between Bordism and Cohomology Spectra
Bordism spectra classify manifolds up to bordism equivalence, capturing geometric information through classes of manifolds and their boundaries, while cohomology spectra represent generalized cohomology theories measuring algebraic invariants of topological spaces. The bordism spectrum is constructed using Thom spectra related to vector bundles, reflecting geometric cobordism relations, whereas cohomology spectra correspond to homotopy types defining cohomology groups with coefficients in ring spectra. Key differences include the emphasis on geometric classification in bordism spectra versus algebraic invariants in cohomology spectra and the distinct construction methods between Thom spectra for bordism and homotopy-theoretic frameworks for cohomology.
Algebraic Structures in Bordism Versus Cohomology
Bordism spectra encode algebraic structures capturing geometric information through cobordism classes with ring and module operations defined via disjoint union and Cartesian product. Cohomology spectra represent generalized cohomology theories equipped with graded ring structures derived from cup product operations, emphasizing algebraic invariants of topological spaces. The interplay between these spectra reveals how bordism's homotopical richness complements cohomology's algebraic formalism, facilitating deep connections in stable homotopy theory and algebraic topology.
Geometric Interpretation of Spectra
Bordism spectra represent stable geometric objects classified by bordism classes of manifolds, encoding cobordism relations through their homotopy groups. Cohomology spectra provide algebraic invariants derived from spaces, interpreting cohomology theories as representable in the stable homotopy category. The geometric interpretation of bordism spectra emphasizes manifold structures and cobordism equivalences, while cohomology spectra focus on generalized cohomological operations and characteristic classes as algebraic reflections of topological features.
Applications of Bordism Spectrum in Topology
The Bordism spectrum plays a crucial role in topology by classifying manifolds up to bordism equivalence, facilitating the detection of topological invariants that are insensitive to smooth structures. It enables the computation of stable homotopy groups and provides a geometric approach to generalized homology theories, connecting with phenomena such as characteristic classes and index theory. Applications include the study of cobordism rings, the formulation of fixed-point theorems, and advancements in stable homotopy theory through spectra like MU and MSO.
Cohomology Spectrum and Its Computational Tools
Cohomology spectra serve as fundamental objects in stable homotopy theory, representing generalized cohomology theories through structured ring spectra. Computational tools for cohomology spectra include spectral sequences such as the Adams and Adams-Novikov spectral sequences, which facilitate the calculation of stable homotopy groups by filtering complex algebraic structures. Software packages like SageMath and specialized libraries for homotopy theory provide frameworks to implement these computations, enabling advances in understanding the algebraic and geometric properties encoded in cohomology spectra.
Interactions and Dualities Between Bordism and Cohomology
Bordism spectra, such as MO or MSO, provide a powerful framework for understanding manifolds through cobordism classes, while cohomology spectra, including ordinary cohomology and extraordinary ones like K-theory, capture algebraic topological invariants of spaces. The interaction between bordism and cohomology is exemplified by the Pontryagin-Thom construction, which establishes a duality connecting geometric bordism classes with homotopy classes of maps into Thom spectra, enabling the translation of geometric problems into homotopical and cohomological terms. This duality manifests in generalized cohomology theories where Thom isomorphisms relate bordism groups to cohomological invariants, facilitating computations and deepening the understanding of manifold topology via spectral sequences and formal group laws.
Recent Developments and Future Directions
Recent developments in bordism spectra emphasize computational techniques using equivariant and motivic homotopy theory to refine the classification of manifolds with additional structures, yielding new connections to stable homotopy groups. Advances in cohomology spectra involve enhanced spectral sequences and derived algebraic geometry, enabling deeper insights into generalized cohomology theories and their applications in chromatic homotopy theory. Future directions anticipate integrating bordism and cohomology spectra frameworks to solve open problems in quantum field theory and string topology, leveraging higher category theory and computational homotopy tools.
Bordism spectrum Infographic
 libterm.com
libterm.com