A mild solution offers gentle and effective relief without harsh chemicals or strong ingredients, making it suitable for sensitive skin or delicate tasks. It ensures comfort while maintaining efficacy, preventing irritation or damage. Explore the rest of the article to discover how a mild solution can benefit your needs.
Table of Comparison
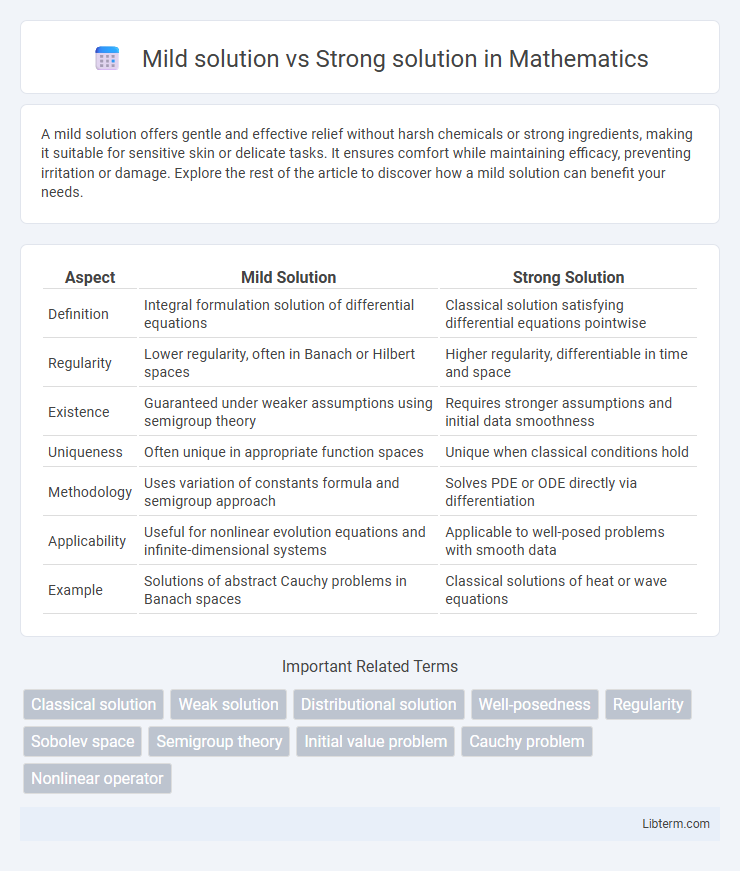
| Aspect | Mild Solution | Strong Solution |
|---|---|---|
| Definition | Integral formulation solution of differential equations | Classical solution satisfying differential equations pointwise |
| Regularity | Lower regularity, often in Banach or Hilbert spaces | Higher regularity, differentiable in time and space |
| Existence | Guaranteed under weaker assumptions using semigroup theory | Requires stronger assumptions and initial data smoothness |
| Uniqueness | Often unique in appropriate function spaces | Unique when classical conditions hold |
| Methodology | Uses variation of constants formula and semigroup approach | Solves PDE or ODE directly via differentiation |
| Applicability | Useful for nonlinear evolution equations and infinite-dimensional systems | Applicable to well-posed problems with smooth data |
| Example | Solutions of abstract Cauchy problems in Banach spaces | Classical solutions of heat or wave equations |
Understanding Mild Solutions and Strong Solutions
Mild solutions refer to solutions of differential equations expressed through integral formulations, typically using semigroup theory, allowing the handling of less regular initial data and ensuring existence where classical solutions may fail. Strong solutions require the function to possess higher regularity, satisfying the differential equation pointwise almost everywhere with well-defined derivatives. Understanding the distinction hinges on the level of regularity and the framework: mild solutions leverage integral equations for broader applicability, while strong solutions rely on direct differentiation and stricter smoothness conditions.
Key Differences Between Mild and Strong Solutions
Mild solutions of differential equations typically involve integral formulations using semigroup theory and are less regular, often existing when classical derivatives do not. Strong solutions require higher regularity and satisfy the differential equation almost everywhere, involving pointwise derivatives. The key difference lies in the degree of smoothness and how the solution fulfills the equation: mild solutions solve an integral equation while strong solutions solve the differential equation in a more classical sense.
Chemical Properties: Mild vs Strong Solutions
Mild solutions typically contain lower concentrations of solutes, resulting in less pronounced chemical reactivity and reduced risk of corrosion or damage to materials. Strong solutions possess higher solute concentrations, leading to greater chemical activity, increased ionic strength, and enhanced ability to participate in chemical reactions or conduct electricity. Understanding the differences in pH, conductivity, and reactivity between mild and strong solutions is essential for applications in chemical manufacturing, pharmaceuticals, and environmental science.
Common Applications of Mild Solutions
Mild solutions are commonly used in the study of partial differential equations (PDEs) where classical solutions may not exist or be difficult to obtain, such as in heat conduction, fluid dynamics, and population models. These solutions leverage semigroup theory to handle evolution equations in Banach spaces, providing a framework for analyzing long-term behavior and stability of systems. Applications in control theory and stochastic PDEs also benefit from mild solutions due to their flexibility in handling less regular initial data and nonlinearities.
Industrial Uses of Strong Solutions
Strong solutions in industrial applications provide precise and reliable models for complex dynamical systems governed by partial differential equations, enabling real-time control and optimization in manufacturing processes. Their ability to guarantee existence, uniqueness, and regularity of solutions makes them essential in fluid dynamics simulations, chemical reaction modeling, and materials science, where accurate predictions impact efficiency and safety. Industries leverage strong solutions for designing advanced control systems, improving system stability, and reducing computational errors in processes such as aerospace engineering, automotive design, and energy production.
Safety Considerations for Mild and Strong Solutions
Mild solutions prioritize low irritancy and reduced chemical concentration, making them safer for sensitive skin and minimizing the risk of adverse reactions. Strong solutions contain higher concentrations of active ingredients, increasing their potency but also raising the potential for skin irritation, burns, or systemic toxicity if not used properly. Proper safety measures, including patch testing, protective gear, and controlled application, are essential when handling strong solutions to prevent harm.
Environmental Impact: Mild vs Strong Solutions
Mild solutions typically employ less aggressive chemicals and processes that reduce harmful emissions and minimize resource consumption, leading to a lower environmental footprint. Strong solutions, while more effective in immediate remediation or industrial efficiency, often involve higher energy usage and produce greater waste or toxic byproducts, which can contribute to environmental degradation. Choosing mild solutions supports sustainable practices by balancing effectiveness with ecological preservation, making them preferable in scenarios prioritizing environmental impact.
Cost Comparison: Mild and Strong Solutions
Mild solutions often require less computational cost and time compared to strong solutions due to their reliance on integral formulations and weaker regularity conditions. Strong solutions demand higher computational resources as they involve solving partial differential equations with stricter smoothness and differentiability requirements. Cost comparison indicates that mild solutions are more efficient for large-scale or complex problems where approximate but feasible solutions are acceptable.
Choosing the Right Solution for Your Needs
Mild solutions and strong solutions differ primarily in their regularity and applicability to differential equations, with mild solutions offering broader existence under weaker conditions and strong solutions providing higher regularity and uniqueness. Choosing the right solution depends on your problem's requirements: use mild solutions when working with less regular initial data or when classical differentiability is difficult to achieve. For precise, well-posed problems where uniqueness and regularity are critical, strong solutions are the preferred choice.
Future Trends in Solution Concentration Usage
Future trends in solution concentration usage emphasize the growing preference for mild solutions due to their enhanced biocompatibility and reduced toxicity, which align with sustainable and green chemistry initiatives. Strong solutions continue to play a critical role in industrial processes requiring high reactivity and efficiency, but advancements in nanotechnology and precision formulation are pushing development towards tailored concentrations that balance potency and safety. Emerging applications in pharmaceuticals and environmental remediation drive innovation toward customizable, concentration-controlled solutions that maximize therapeutic efficacy while minimizing adverse effects.
Mild solution Infographic
 libterm.com
libterm.com