Selecting the exact category for your product or service significantly enhances its visibility and search engine optimization. Proper categorization ensures that potential customers quickly find what they need, improving your website's relevance and user experience. Explore the rest of the article to discover strategies for identifying the perfect category that fits Your offerings.
Table of Comparison
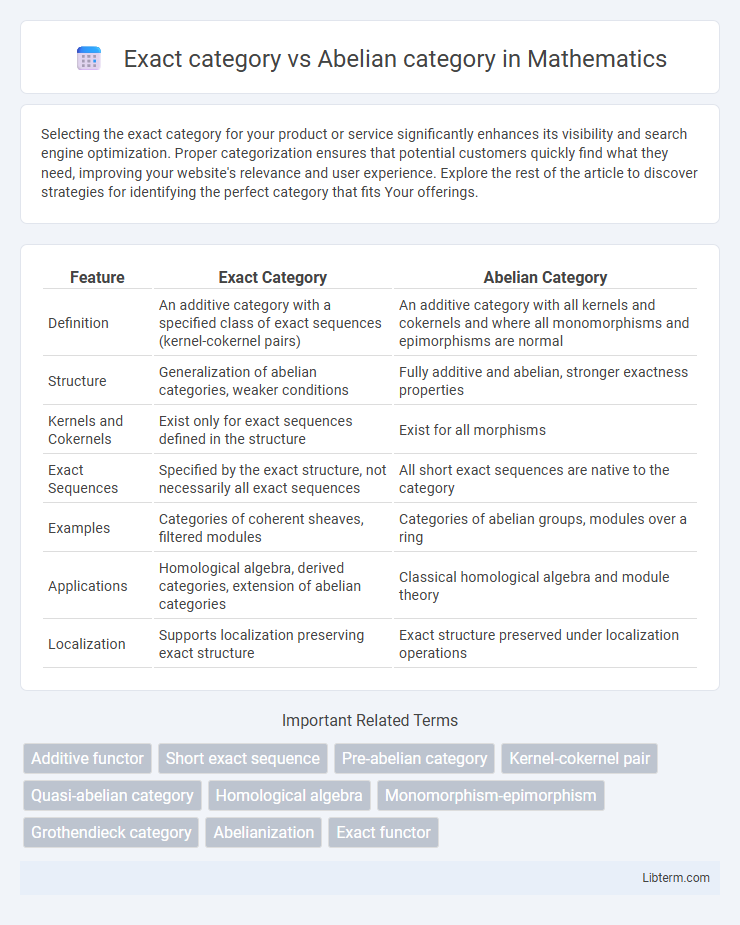
| Feature | Exact Category | Abelian Category |
|---|---|---|
| Definition | An additive category with a specified class of exact sequences (kernel-cokernel pairs) | An additive category with all kernels and cokernels and where all monomorphisms and epimorphisms are normal |
| Structure | Generalization of abelian categories, weaker conditions | Fully additive and abelian, stronger exactness properties |
| Kernels and Cokernels | Exist only for exact sequences defined in the structure | Exist for all morphisms |
| Exact Sequences | Specified by the exact structure, not necessarily all exact sequences | All short exact sequences are native to the category |
| Examples | Categories of coherent sheaves, filtered modules | Categories of abelian groups, modules over a ring |
| Applications | Homological algebra, derived categories, extension of abelian categories | Classical homological algebra and module theory |
| Localization | Supports localization preserving exact structure | Exact structure preserved under localization operations |
Introduction to Algebraic Categories
Exact categories generalize abelian categories by relaxing the requirement that every morphism has kernels and cokernels, capturing a broader class of additive categories with a well-behaved notion of short exact sequences. Abelian categories serve as the foundational framework in algebraic categories due to their complete exactness properties, including all finite limits and colimits and the existence of enough injectives and projectives. Understanding the subtle distinctions between exact and abelian categories is crucial in homological algebra, where exact categories allow the study of relative homological algebra and derived categories beyond classical abelian settings.
Defining Exact Categories
An exact category is a pair (A, E) where A is an additive category and E is a class of kernel-cokernel pairs called conflations that satisfy axioms resembling short exact sequences in abelian categories. Unlike abelian categories, exact categories do not require all morphisms to have kernels and cokernels but ensure enough structure to define extensions and homological algebra. This framework generalizes abelian categories by allowing exact sequences in contexts where full abelian properties are too restrictive, facilitating work in triangulated and derived categories.
Overview of Abelian Categories
Abelian categories provide a generalized framework for homological algebra, characterized by the existence of kernels, cokernels, and exact sequences that mimic properties of modules over a ring. Unlike exact categories, which focus on admissible monomorphisms and epimorphisms to define exactness, Abelian categories demand all morphisms have kernels and cokernels, ensuring every monomorphism and epimorphism is normal. This structure guarantees that morphisms factor uniquely through their images and coimages, enabling a rich theory of exact sequences and homological functors critical in algebra and geometry.
Core Properties of Exact Categories
Exact categories generalize abelian categories by relaxing requirements while retaining a structured concept of exact sequences defined via kernel-cokernel pairs called conflations. Core properties include closure under extensions, existence of inflation and deflation morphisms, and stability under pushouts and pullbacks along these morphisms, enabling homological algebra methods in more general settings. Unlike abelian categories, exact categories need not have all kernels and cokernels but maintain a precise axiomatic framework to handle exactness and short exact sequences.
Fundamental Features of Abelian Categories
Abelian categories are additive categories equipped with kernels and cokernels for every morphism, ensuring every monomorphism and epimorphism is normal and enabling exact sequences. Unlike exact categories, which generalize exactness via a chosen class of admissible short exact sequences, abelian categories guarantee all morphisms factor as a composition of an epimorphism followed by a monomorphism. This intrinsic exactness structure facilitates homological algebra and underpins fundamental concepts such as derived functors and cohomology theories.
Comparing Exact and Abelian Categories
Exact categories generalize abelian categories by relaxing requirements on kernels and cokernels, allowing for a broader class of additive categories with exact sequences defined by a specific class of admissible monomorphisms and epimorphisms. Abelian categories require every morphism to have a kernel and cokernel, ensuring all exact sequences arise from these morphisms, which provides a more rigid and structured framework for homological algebra. Exact categories enable the study of relative homological algebra where abelian properties do not fully apply, making them crucial in contexts such as representation theory and algebraic geometry where more flexible exactness conditions are needed.
Examples of Exact Categories in Mathematics
Exact categories generalize abelian categories by weakening some axioms while retaining a well-behaved notion of exact sequences. Examples of exact categories include the category of projective modules over a ring, extension-closed subcategories of abelian categories, and the category of coherent sheaves on a non-noetherian scheme. These structures allow homological methods in settings where abelian categories are too restrictive, enabling deeper exploration of derived and triangulated categories.
Illustrative Examples of Abelian Categories
Abelian categories, such as the category of abelian groups, the category of modules over a ring, and the category of coherent sheaves on a scheme, provide a rich framework with exact sequences enabling homological algebra. Unlike exact categories, which generalize exactness without requiring all kernels and cokernels, abelian categories guarantee the existence of all finite limits and colimits, including kernels and cokernels. These features allow abelian categories to support powerful tools like derived functors and cohomology theories, making them central in algebraic geometry and representation theory.
Applications and Importance in Homological Algebra
Exact categories generalize abelian categories by relaxing the requirement for all kernels and cokernels to exist while still supporting a well-behaved notion of exact sequences, enabling broader applicability in contexts like algebraic K-theory and representation theory. Abelian categories provide a robust framework with all limits, colimits, and exact sequences, serving as the foundational setting for classical homological algebra techniques such as derived functors and Ext and Tor groups. The distinction between exact and abelian categories allows mathematicians to extend homological methods to new algebraic structures where abelian assumptions fail but exact sequences remain meaningful, thus deepening the understanding of derived categories and triangulated categories.
Key Differences and When to Use Each Category
Exact categories generalize abelian categories by allowing weaker exactness conditions, specifically identifying a class of "admissible" monomorphisms and epimorphisms without requiring all kernels and cokernels to exist. Abelian categories are exact categories with the strongest exactness properties, including all finite limits and colimits, making them ideal for homological algebra and well-behaved module categories. Use exact categories for more flexible settings like relative homological algebra or when working with subcategories lacking full abelian structure, while abelian categories are preferred for classical homological theories and representation theory where robust exactness properties simplify analysis.
Exact category Infographic
 libterm.com
libterm.com