A developable surface is a type of geometric surface that can be unfolded or flattened onto a plane without distortion, preserving lengths and angles. Common examples include cylinders, cones, and tangent developables, crucial in fields like architecture, manufacturing, and computer graphics for material optimization and design accuracy. Explore this article to understand how developable surfaces impact your design projects and practical applications.
Table of Comparison
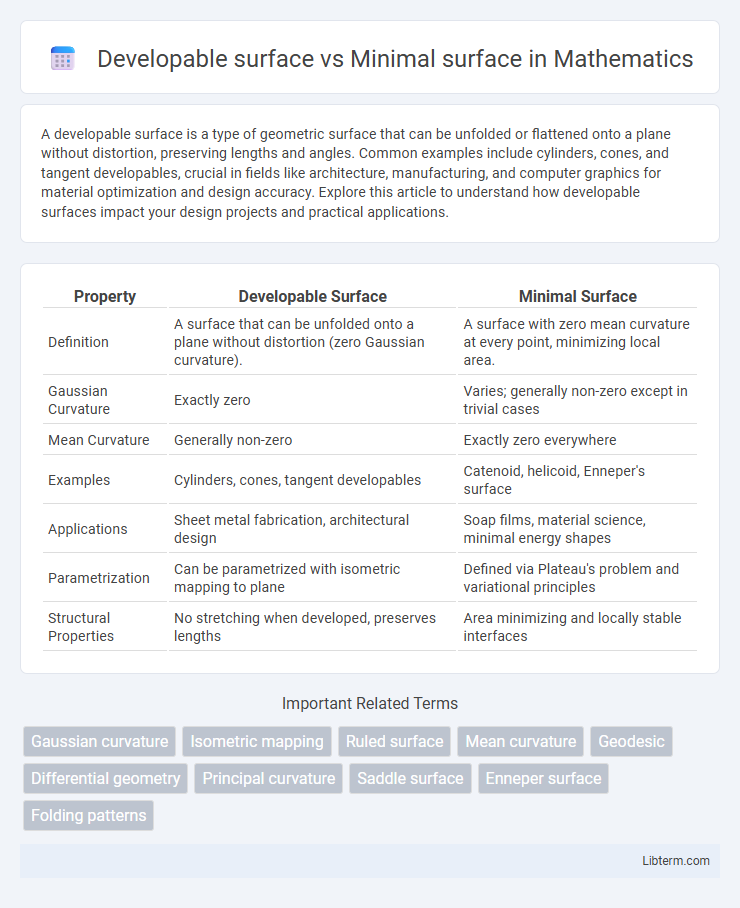
| Property | Developable Surface | Minimal Surface |
|---|---|---|
| Definition | A surface that can be unfolded onto a plane without distortion (zero Gaussian curvature). | A surface with zero mean curvature at every point, minimizing local area. |
| Gaussian Curvature | Exactly zero | Varies; generally non-zero except in trivial cases |
| Mean Curvature | Generally non-zero | Exactly zero everywhere |
| Examples | Cylinders, cones, tangent developables | Catenoid, helicoid, Enneper's surface |
| Applications | Sheet metal fabrication, architectural design | Soap films, material science, minimal energy shapes |
| Parametrization | Can be parametrized with isometric mapping to plane | Defined via Plateau's problem and variational principles |
| Structural Properties | No stretching when developed, preserves lengths | Area minimizing and locally stable interfaces |
Introduction to Developable and Minimal Surfaces
Developable surfaces are characterized by zero Gaussian curvature, allowing them to be unfolded into a plane without distortion and commonly found in materials like metal sheets or paper. Minimal surfaces, defined by zero mean curvature, represent surfaces that minimize area locally and often arise in physical phenomena such as soap films spanning wire frames. Both surfaces play crucial roles in differential geometry and practical applications, with developable surfaces emphasizing bending without stretching and minimal surfaces emphasizing geometric optimization of surface area.
Fundamental Definitions
Developable surfaces are characterized by zero Gaussian curvature, meaning they can be unfolded onto a plane without distortion, commonly seen in cylinders and cones. Minimal surfaces are defined by mean curvature equal to zero at every point, representing surfaces that locally minimize area, such as the catenoid and helicoid. The fundamental distinction lies in developable surfaces preserving intrinsic distances through isometric mapping, while minimal surfaces represent equilibrium states in variational problems governed by the calculus of variations.
Mathematical Properties of Developable Surfaces
Developable surfaces are characterized by zero Gaussian curvature, allowing them to be flattened onto a plane without distortion, unlike minimal surfaces which minimize mean curvature and exhibit saddle-like geometry. Mathematically, developable surfaces are ruled surfaces generated by moving a straight line, with the property that their Gaussian curvature K = 0 everywhere, making them intrinsically flat. These surfaces satisfy the Monge-Ampere equation det(D2f) = 0, distinguishing them from minimal surfaces that solve the minimal surface equation Df = 0.
Mathematical Properties of Minimal Surfaces
Minimal surfaces are characterized by zero mean curvature at every point, distinguishing them from developable surfaces, which have zero Gaussian curvature but nonzero mean curvature except along rulings. These surfaces solve variational problems by locally minimizing surface area and satisfy the minimal surface equation, a nonlinear partial differential equation derived from the calculus of variations. Unlike developable surfaces that can be unfolded into a plane without distortion, minimal surfaces exhibit intrinsic curvature that prohibits such isometric mapping.
Key Differences between Developable and Minimal Surfaces
Developable surfaces have zero Gaussian curvature and can be flattened onto a plane without distortion, making them ideal for applications in sheet metal fabrication and architectural design. Minimal surfaces minimize surface area for a given boundary, characterized by zero mean curvature, often found in natural soap films and used in structural optimization. The key difference lies in curvature properties: developable surfaces possess zero Gaussian curvature, while minimal surfaces maintain zero mean curvature, influencing their geometric behavior and practical uses.
Geometric Visualization and Representation
Developable surfaces can be unfolded into a plane without distortion, making them ideal for applications in manufacturing and architectural design where precise geometric representation is critical. Minimal surfaces, characterized by zero mean curvature, illustrate complex geometric visualization with smooth, saddle-shaped forms that minimize surface area while maintaining structural integrity. Effective representation techniques leverage differential geometry and parametric modeling to capture the intrinsic properties of both surface types, facilitating accurate simulations and practical implementations.
Real-world Applications of Developable Surfaces
Developable surfaces, such as cylinders and cones, are essential in manufacturing industries for creating materials that can be formed from flat sheets without stretching, enabling efficient fabrication of metal panels, ship hulls, and architectural cladding. Unlike minimal surfaces, which minimize surface area and are primarily studied for their mathematical properties and applications in materials science, developable surfaces provide practical solutions in automotive bodywork and paper modeling due to their ability to unfold into flat patterns. This property of developable surfaces facilitates accurate cutting, bending, and assembly processes, reducing waste and improving structural integrity in real-world engineering and design projects.
Real-world Applications of Minimal Surfaces
Minimal surfaces, characterized by zero mean curvature and elegant geometric properties, find extensive real-world applications in architecture and materials science due to their ability to form stable, lightweight structures with minimal material usage. Unlike developable surfaces that can be flattened without distortion, minimal surfaces such as soap films and catenoids optimize surface area, supporting innovations in tensile membrane structures, aerospace design, and biomedical scaffolds. Their unique balance of strength and efficiency drives advanced engineering solutions that leverage natural minimal-energy configurations for sustainable and cost-effective design.
Comparative Advantages and Limitations
Developable surfaces, characterized by zero Gaussian curvature, allow for isometric mapping of flat materials such as metal sheets, enabling efficient fabrication with minimal material distortion. Minimal surfaces minimize surface area under boundary constraints, offering superior structural efficiency and aesthetic appeal in architectural and engineering applications but require complex manufacturing techniques due to their double curvature. While developable surfaces excel in manufacturing simplicity and cost-effectiveness, minimal surfaces provide enhanced mechanical performance and fluid dynamics optimization, posing challenges in fabrication and material usage.
Future Directions in Surface Geometry Research
Future directions in surface geometry research emphasize the exploration of developable surfaces for advanced manufacturing and architectural applications due to their unique property of zero Gaussian curvature enabling material flattening without distortion. Concurrently, minimal surfaces, characterized by mean curvature zero and optimal area properties, are investigated for innovations in biomimetic structures and energy-efficient material designs. Integrating computational methods with differential geometry promises breakthroughs in hybrid surface modeling, optimizing both structural efficiency and manufacturability in complex geometric designs.
Developable surface Infographic
 libterm.com
libterm.com