Topological space is a fundamental concept in mathematics that generalizes the notions of convergence, continuity, and boundary through a set equipped with a collection of open sets satisfying specific axioms. Understanding the properties and structures of topological spaces allows you to navigate complex areas in analysis, geometry, and beyond. Explore the rest of the article to deepen your grasp of topological spaces and their applications.
Table of Comparison
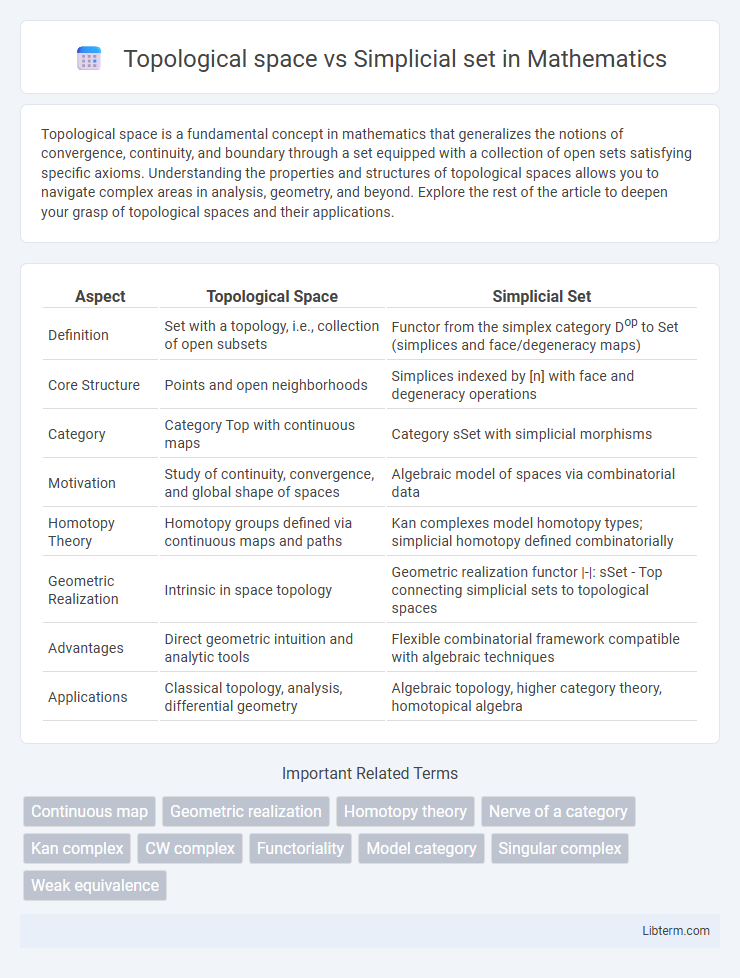
| Aspect | Topological Space | Simplicial Set |
|---|---|---|
| Definition | Set with a topology, i.e., collection of open subsets | Functor from the simplex category Dop to Set (simplices and face/degeneracy maps) |
| Core Structure | Points and open neighborhoods | Simplices indexed by [n] with face and degeneracy operations |
| Category | Category Top with continuous maps | Category sSet with simplicial morphisms |
| Motivation | Study of continuity, convergence, and global shape of spaces | Algebraic model of spaces via combinatorial data |
| Homotopy Theory | Homotopy groups defined via continuous maps and paths | Kan complexes model homotopy types; simplicial homotopy defined combinatorially |
| Geometric Realization | Intrinsic in space topology | Geometric realization functor |-|: sSet - Top connecting simplicial sets to topological spaces |
| Advantages | Direct geometric intuition and analytic tools | Flexible combinatorial framework compatible with algebraic techniques |
| Applications | Classical topology, analysis, differential geometry | Algebraic topology, higher category theory, homotopical algebra |
Introduction to Topological Spaces and Simplicial Sets
Topological spaces are fundamental structures in mathematics defined by a set of points along with a topology, a collection of open subsets satisfying union, intersection, and inclusion properties, providing a framework for continuity and convergence. Simplicial sets are combinatorial models of topological spaces built from simplices--vertices, edges, triangles, and their higher-dimensional analogs--organized via face and degeneracy maps, allowing algebraic and categorical manipulations. Both concepts serve to study shape and structure, with topological spaces emphasizing geometric intuition and simplicial sets enabling discrete, algebraic approaches in homotopy theory and algebraic topology.
Fundamental Concepts and Definitions
Topological spaces consist of a set equipped with a collection of open subsets satisfying union, intersection, and inclusion axioms that define continuous deformations. Simplicial sets are combinatorial structures built from simplices connected by face and degeneracy maps, encoding spatial information algebraically. The fundamental group and homotopy type can be studied in both frameworks, with simplicial sets providing a discrete and categorical perspective on topological invariants.
Motivation: Why Compare Topological Spaces and Simplicial Sets?
Comparing topological spaces and simplicial sets reveals fundamental differences in how geometric and combinatorial structures encode homotopy information and continuous transformations. Topological spaces provide a classical framework for studying continuity and convergence, while simplicial sets offer a combinatorial model that simplifies complex homotopy computations and categorical interpretations. Understanding their interplay motivates advances in algebraic topology, enabling more efficient methods for modeling spaces and mapping homotopies.
Building Blocks: Points, Open Sets, and Simplices
Topological spaces are built from points and open sets, where open sets define the structure and continuity of the space. Simplicial sets use simplices--points, line segments, triangles, and higher-dimensional analogues--as combinatorial building blocks to model spaces algebraically. The fundamental difference lies in topology's reliance on open sets for spatial relationships, while simplicial sets encode these relationships through face and degeneracy maps connecting simplices.
Morphisms: Continuous Maps vs. Simplicial Maps
Morphisms in topological spaces are continuous maps that preserve the structure of open sets, ensuring the preimage of every open set remains open. In contrast, simplicial sets use simplicial maps, which are functions between sets of simplices that maintain the face and degeneracy relations, reflecting combinatorial structure. Continuous maps enable geometric intuition in topology, while simplicial maps facilitate algebraic manipulation in combinatorial topology and higher category theory.
Homotopy and Homology in Both Structures
Topological spaces and simplicial sets both serve as fundamental frameworks for studying homotopy and homology, with topological spaces relying on continuous maps and deformation retracts to analyze homotopy groups and singular homology. Simplicial sets, composed of combinatorial data via simplices and face/degeneracy maps, facilitate an algebraic approach to homotopy theory through Kan complexes and model category structures, providing explicit simplicial homotopy and homology computations. The equivalence between the homotopy categories of topological spaces and simplicial sets, established by geometric realization and singular functor adjunctions, underscores the importance of these structures in algebraic topology and their complementary roles in understanding topological invariants.
Advantages of Topological Spaces
Topological spaces offer a flexible framework for studying continuity, convergence, and neighborhood structures with intuitive geometric and analytical interpretations. Their well-established theory enables straightforward applications in classical analysis, differential geometry, and algebraic topology. Unlike simplicial sets, topological spaces provide direct access to concepts like open and closed sets, making them particularly advantageous for handling problems involving limits and continuity.
Benefits of Simplicial Sets
Simplicial sets offer a combinatorial framework that simplifies complex topological problems by encoding spaces through simplices and face/degeneracy maps, enabling more effective computational manipulation. Unlike traditional topological spaces, simplicial sets facilitate homotopy-theoretic analysis with explicit algebraic structures that improve the study of higher-dimensional categories and homotopy types. Their categorical nature supports easier modeling of colimits and limits, making them powerful tools in abstract homotopy theory and algebraic topology.
Key Differences and Applications
Topological spaces provide a continuous framework for studying spaces using open sets, while simplicial sets offer a combinatorial approach based on simplices and face/degeneracy maps. Key differences include the use of geometric intuition in topological spaces versus algebraic and categorical structures in simplicial sets, which make them ideal for homotopy theory and higher category theory. Applications of topological spaces span classical analysis and geometry, whereas simplicial sets are crucial in algebraic topology, including the study of homotopy limits and the development of model categories.
Conclusion: Choosing the Right Framework
Selecting between a topological space and a simplicial set depends on the specific requirements of your mathematical or computational problem, especially in algebraic topology or homotopy theory. Topological spaces provide a more intuitive geometric framework suitable for continuous structures, whereas simplicial sets offer a combinatorial model ideal for discrete and categorical methods. Choosing the right framework involves balancing geometric intuition against algebraic flexibility, with simplicial sets often preferred for computational homotopy and higher category theory applications.
Topological space Infographic
 libterm.com
libterm.com