Convergence in probability is a fundamental concept in statistics that describes how a sequence of random variables becomes arbitrarily close to a specific value as the sample size increases. This form of convergence is crucial for understanding the behavior of estimators and ensuring the reliability of statistical inference. Explore the rest of the article to deepen your understanding of convergence in probability and its practical applications.
Table of Comparison
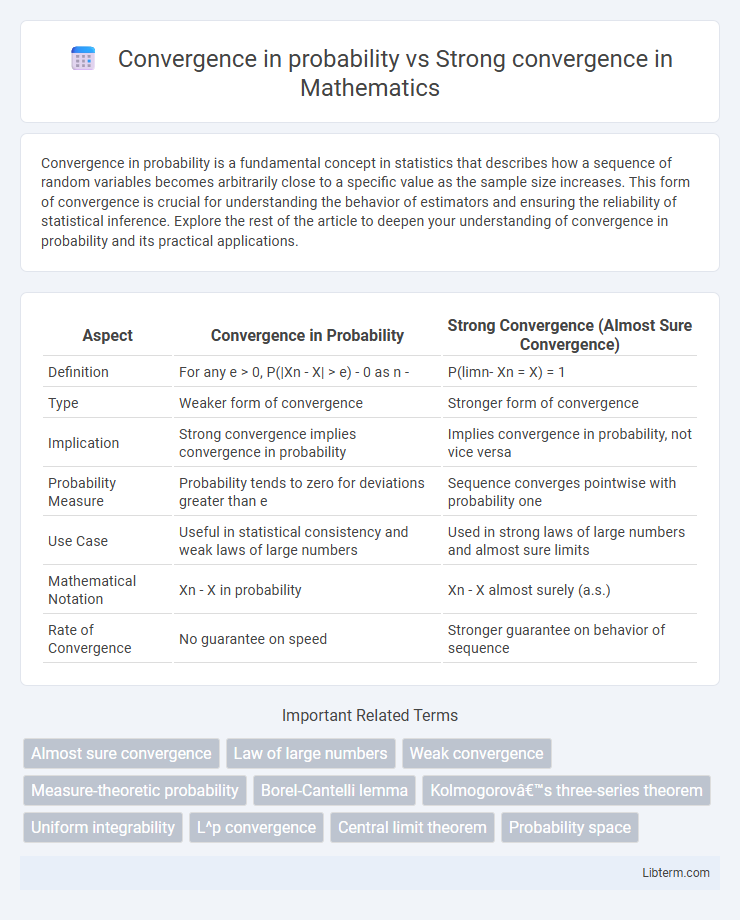
| Aspect | Convergence in Probability | Strong Convergence (Almost Sure Convergence) |
|---|---|---|
| Definition | For any e > 0, P(|Xn - X| > e) - 0 as n - | P(limn- Xn = X) = 1 |
| Type | Weaker form of convergence | Stronger form of convergence |
| Implication | Strong convergence implies convergence in probability | Implies convergence in probability, not vice versa |
| Probability Measure | Probability tends to zero for deviations greater than e | Sequence converges pointwise with probability one |
| Use Case | Useful in statistical consistency and weak laws of large numbers | Used in strong laws of large numbers and almost sure limits |
| Mathematical Notation | Xn - X in probability | Xn - X almost surely (a.s.) |
| Rate of Convergence | No guarantee on speed | Stronger guarantee on behavior of sequence |
Introduction to Convergence Concepts
Convergence in probability describes a sequence of random variables approaching a fixed random variable such that for any positive epsilon, the probability that their difference exceeds epsilon converges to zero. Strong convergence, or almost sure convergence, requires that the sequence converges to the random variable with probability one, meaning the values eventually stay arbitrarily close almost everywhere. These fundamental concepts highlight the differences in stochastic limit behavior, underpinning theorems in probability theory and statistics.
Definitions: Convergence in Probability
Convergence in probability occurs when the probability that a sequence of random variables deviates from a fixed value by more than any positive threshold approaches zero as the sequence progresses. Formally, a sequence {X_n} converges in probability to X if for every e > 0, the limit of P(|X_n - X| > e) as n approaches infinity is zero. This concept ensures that the values of X_n become arbitrarily close to X with high probability but does not guarantee almost sure convergence.
Definitions: Strong Convergence (Almost Sure Convergence)
Strong convergence, or almost sure convergence, occurs when a sequence of random variables \(X_n\) converges to a random variable \(X\) with probability 1, meaning \(P(\lim_{n \to \infty} X_n = X) = 1\). This type of convergence implies that the values of \(X_n\) will eventually be arbitrarily close to \(X\) for almost every outcome in the sample space. Unlike convergence in probability, strong convergence guarantees convergence for individual sample paths rather than just in distribution or probability.
Key Differences Between the Two Convergences
Convergence in probability means that for any positive epsilon, the probability that the difference between the sequence and the limit exceeds epsilon approaches zero as the index goes to infinity. Strong convergence, often called almost sure convergence, requires that the sequence converges to the limit with probability one, meaning the event of non-convergence has zero probability. The key difference is that strong convergence implies convergence in probability, but convergence in probability does not guarantee strong convergence, reflecting a hierarchy in modes of convergence in probability theory.
Formal Mathematical Statements
Convergence in probability of a sequence of random variables \(X_n\) to \(X\) is formally defined as \(\forall \epsilon > 0, \lim_{n \to \infty} P(|X_n - X| > \epsilon) = 0\). Strong convergence, or almost sure convergence, requires that \(P\left(\lim_{n \to \infty} X_n = X\right) = 1\), meaning the sequence \(X_n\) converges to \(X\) almost everywhere. Strong convergence implies convergence in probability by the Borel-Cantelli lemma, but the converse generally does not hold without additional assumptions.
Practical Examples and Illustrations
Convergence in probability occurs when the probability that a sequence of random variables differs from a target variable by more than a small amount approaches zero, often illustrated by the law of large numbers where the sample mean converges to the population mean as the sample size increases. Strong convergence, or almost sure convergence, demands that the sequence converges to the target variable with probability one, exemplified by scenarios such as the almost sure convergence of random walks normalized by their number of steps. Practical examples include convergence in probability when approximating parameters with large samples in statistics, versus strong convergence observed in stochastic algorithms like Monte Carlo simulations that require guaranteed long-term behavior.
Hierarchy of Modes of Convergence
Strong convergence, also known as almost sure convergence, implies that a sequence of random variables converges to a limit with probability one, representing the strongest form of convergence in probability theory. Convergence in probability is weaker, requiring that for every positive epsilon, the probability that the sequence deviates from the limit by more than epsilon approaches zero as the sample size grows. The hierarchy of modes of convergence places almost sure convergence above convergence in probability, which in turn is stronger than convergence in distribution but weaker than L^p convergence for p >= 1.
Implications in Probability Theory
Convergence in probability implies that for any positive epsilon, the probability that the sequence deviates from the limit by more than epsilon approaches zero, ensuring a weaker form of convergence used extensively in the Law of Large Numbers. Strong convergence, or almost sure convergence, guarantees that the sequence converges to the limit with probability one, providing a stronger condition critical for results like the Strong Law of Large Numbers. Understanding the distinction is essential for applying limit theorems and analyzing stochastic processes in probability theory.
Applications in Statistics and Data Science
Convergence in probability ensures that estimators approach the true parameter value as sample size increases, making it essential for consistency in statistical inference and large-sample theory. Strong convergence, or almost sure convergence, provides stronger guarantees of estimator behavior, crucial for developing robust algorithms in machine learning that require stability across iterations. Both types of convergence underpin the reliability of predictive models, hypothesis testing, and the asymptotic analysis of algorithms in data science.
Summary and Key Takeaways
Convergence in probability occurs when the probability that a sequence of random variables deviates from the limit by any positive amount approaches zero, emphasizing "eventual closeness" in a probabilistic sense. Strong convergence, or almost sure convergence, requires that the sequence converges to the limit with probability one, ensuring pointwise convergence almost everywhere. Understanding the difference hinges on recognizing that strong convergence implies convergence in probability, but not vice versa, highlighting different modes of stochastic convergence crucial in probability theory and statistical inference.
Convergence in probability Infographic
 libterm.com
libterm.com