Topology explores properties of space that remain unchanged under continuous deformations such as stretching or bending, without tearing or gluing. It plays a crucial role in various fields including mathematics, physics, and computer science, helping to understand shapes, surfaces, and spatial relationships. Delve deeper into the article to discover how topology impacts your understanding of the world around you.
Table of Comparison
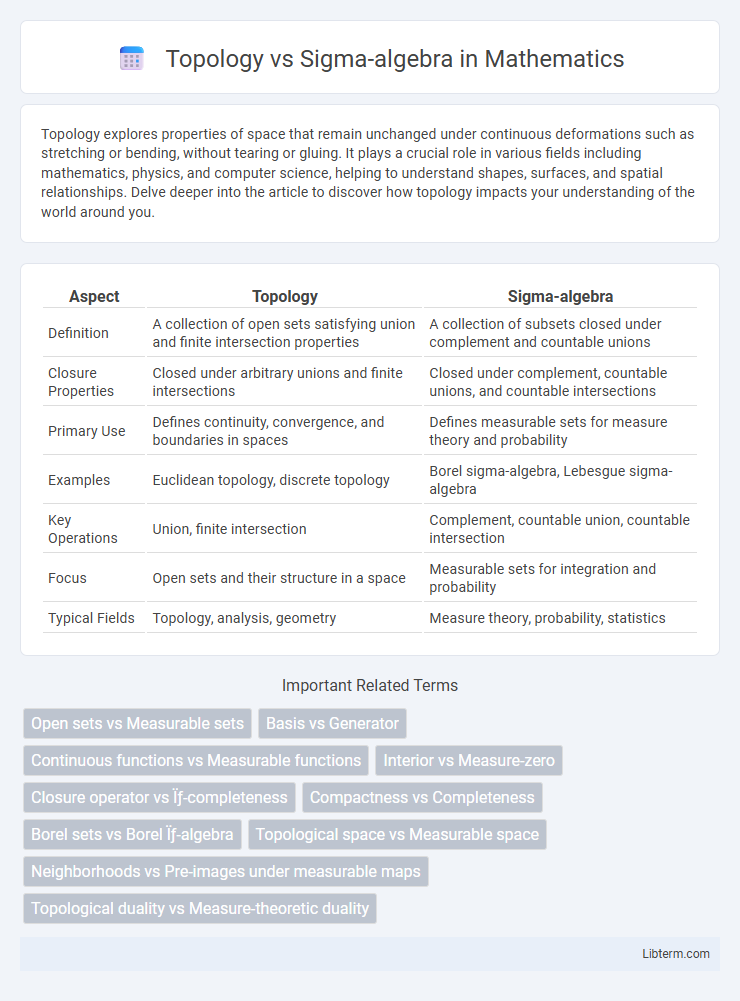
| Aspect | Topology | Sigma-algebra |
|---|---|---|
| Definition | A collection of open sets satisfying union and finite intersection properties | A collection of subsets closed under complement and countable unions |
| Closure Properties | Closed under arbitrary unions and finite intersections | Closed under complement, countable unions, and countable intersections |
| Primary Use | Defines continuity, convergence, and boundaries in spaces | Defines measurable sets for measure theory and probability |
| Examples | Euclidean topology, discrete topology | Borel sigma-algebra, Lebesgue sigma-algebra |
| Key Operations | Union, finite intersection | Complement, countable union, countable intersection |
| Focus | Open sets and their structure in a space | Measurable sets for integration and probability |
| Typical Fields | Topology, analysis, geometry | Measure theory, probability, statistics |
Introduction to Topology and Sigma-Algebra
Topology studies the properties of spaces through open sets, focusing on concepts like continuity, convergence, and boundary without relying on measure. Sigma-algebra is a collection of sets closed under countable unions, intersections, and complements, essential for defining measurable spaces and integrating functions in probability theory. Both structures provide foundational frameworks for analysis, yet topology addresses spatial relations while sigma-algebra underpins measure-theoretic approaches.
Key Definitions: Topology and Sigma-Algebra
Topology is a collection of open sets on a given set that is closed under finite intersections and arbitrary unions, defining the structure of continuous spaces. Sigma-algebra is a collection of subsets closed under complement and countable unions, serving as the foundational structure for measure theory and probability. The key difference lies in their closure properties: topology emphasizes open set operations, while sigma-algebra focuses on measurable sets and countable operations.
Fundamental Concepts in Topology
Topology centers on open sets, neighborhoods, and continuity, providing the framework for convergence and connectedness in mathematical spaces. Sigma-algebra focuses on collections of sets closed under countable unions, intersections, and complements, essential for defining measures and integrating functions. Fundamental concepts in topology include open and closed sets, basis, subbasis, and separation axioms, which differ from sigma-algebra's measurable sets and operations fundamental to measure theory.
Essential Properties of Sigma-Algebras
Sigma-algebras are collections of subsets closed under complementation and countable unions, essential for defining measure spaces in probability theory. They include the entire set and are closed under countable intersections due to closure under complementation and unions, enabling rigorous treatment of measurable events. Unlike topologies, which emphasize open sets and continuity, sigma-algebras prioritize closure properties that facilitate defining measures and integrating functions.
Topology vs Sigma-Algebra: Structural Differences
Topology and sigma-algebra differ fundamentally in their structural properties: topology involves open sets closed under finite intersections and arbitrary unions, while sigma-algebra requires closure under complements and countable unions. Topologies emphasize continuity and convergence through open sets, whereas sigma-algebras focus on measurable sets for integration and probability theory. These differences delineate their application domains, with topology underpinning geometric spaces and sigma-algebras forming the basis of measure theory.
Set Operations in Topology and Sigma-Algebra
Topology and sigma-algebra both involve collections of subsets closed under specific set operations, but their closure properties differ fundamentally. In topology, the family of open sets is closed under arbitrary unions and finite intersections, emphasizing the structure of continuity and convergence. Sigma-algebra requires closure under countable unions, countable intersections, and complements, which supports measure-theoretic frameworks and probability theory.
Applications of Topology in Mathematics
Topology provides a framework for analyzing continuity, convergence, and boundary properties essential in fields such as analysis, differential geometry, and dynamical systems. Unlike sigma-algebras, which primarily underpin measure theory and probability through measurable sets and integrals, topological spaces enable the study of spatial properties and global structure without relying on measures. Key applications include the classification of manifolds, fixed point theorems in nonlinear analysis, and modern approaches to functional spaces in mathematical physics and algebraic topology.
Applications of Sigma-Algebra in Probability Theory
Sigma-algebras are fundamental in probability theory as they provide the rigorous framework for defining measurable events and constructing probability measures, enabling the formal treatment of random variables and expectation. Unlike topologies, which focus on open sets and continuity, sigma-algebras prioritize closure under countable unions and complements, ensuring well-defined probabilities for complex event combinations. This structure underpins key concepts such as conditional probability, independence, and measurable functions, making sigma-algebras indispensable for stochastic processes and statistical inference.
Examples Illustrating Topology and Sigma-Algebra
A topology on a set X can be exemplified by the standard topology on the real numbers, where the open sets include open intervals like (a, b), whereas a sigma-algebra on X, such as the Borel sigma-algebra, contains all open sets and is closed under countable unions, intersections, and complements. For instance, the power set of X is a sigma-algebra containing every subset of X, showing maximal closure properties, while a topology need only satisfy closure under finite intersections and arbitrary unions. These examples highlight that topologies focus on openness and continuity concepts, while sigma-algebras emphasize measurability and probabilistic structure.
Conclusion: Comparing Topology and Sigma-Algebra
Topology and sigma-algebra both provide frameworks for organizing sets but serve distinct purposes: topology focuses on continuity and limit processes using open sets, while sigma-algebra structures measurable sets for integration and probability. The key difference lies in closure properties--topologies are closed under finite intersections and arbitrary unions, whereas sigma-algebras require closure under countable unions, intersections, and complements. Understanding these fundamental contrasts is essential for applications in analysis, measure theory, and probability theory.
Topology Infographic
 libterm.com
libterm.com