The fpqc topology (faithfully flat quasi-compact topology) is a Grothendieck topology used in algebraic geometry, where covers consist of faithfully flat and quasi-compact morphisms of schemes. This topology is essential for studying descent theory, allowing one to glue schemes and sheaves over faithfully flat coverings. Explore the rest of the article to understand how the fpqc topology facilitates advanced constructions in scheme theory and descent.
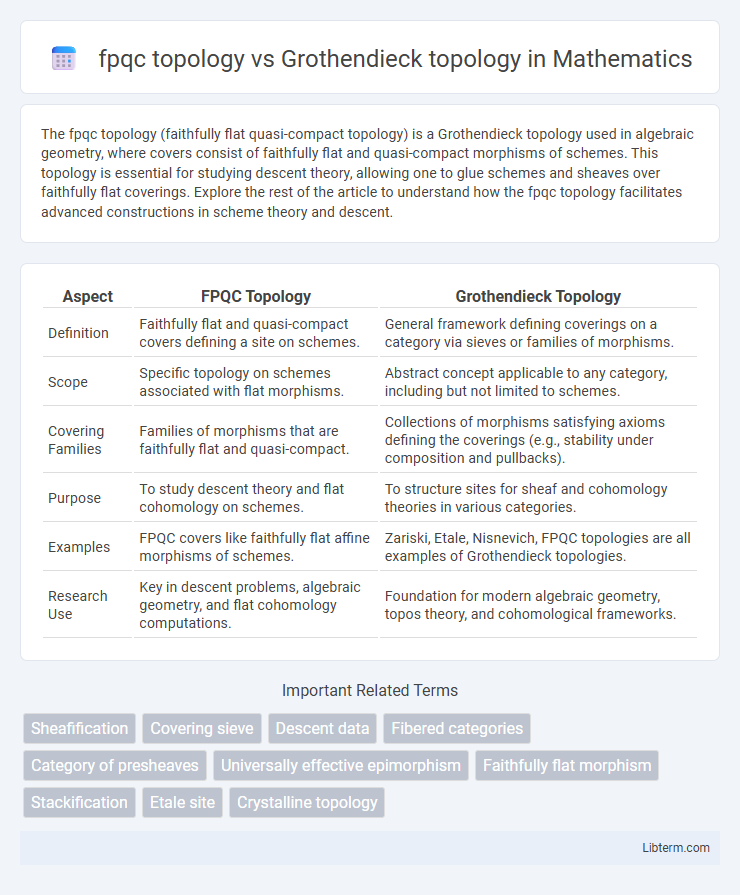
Table of Comparison
| Aspect | FPQC Topology | Grothendieck Topology |
|---|---|---|
| Definition | Faithfully flat and quasi-compact covers defining a site on schemes. | General framework defining coverings on a category via sieves or families of morphisms. |
| Scope | Specific topology on schemes associated with flat morphisms. | Abstract concept applicable to any category, including but not limited to schemes. |
| Covering Families | Families of morphisms that are faithfully flat and quasi-compact. | Collections of morphisms satisfying axioms defining the coverings (e.g., stability under composition and pullbacks). |
| Purpose | To study descent theory and flat cohomology on schemes. | To structure sites for sheaf and cohomology theories in various categories. |
| Examples | FPQC covers like faithfully flat affine morphisms of schemes. | Zariski, Etale, Nisnevich, FPQC topologies are all examples of Grothendieck topologies. |
| Research Use | Key in descent problems, algebraic geometry, and flat cohomology computations. | Foundation for modern algebraic geometry, topos theory, and cohomological frameworks. |
Introduction to Topologies in Algebraic Geometry
FPQC topology, a refinement within the framework of Grothendieck topologies, specializes in coverings defined by faithfully flat and quasi-compact morphisms, crucial for descent theory and algebraic stack constructions. Grothendieck topologies generalize classical topological notions to categorical settings, enabling the definition of sheaves on schemes through covering families that satisfy specific axioms, including Zariski, etale, and fpqc topologies. Understanding these topologies facilitates a deep grasp of geometric objects in algebraic geometry by providing tools for local-global principles and cohomological methods.
Overview of Grothendieck Topologies
Grothendieck topologies generalize classical topological spaces by defining coverings through commutative algebraic structures, providing a flexible framework for sheaf theory on categories beyond sets. The fpqc (faithfully flat quasi-compact) topology is a specific Grothendieck topology focused on schemes, utilizing faithfully flat and quasi-compact morphisms to capture descent data. Unlike classical topologies, Grothendieck topologies like fpqc emphasize morphism properties, enabling the study of algebraic geometry and cohomology in deeper categorical contexts.
Defining the fpqc Topology
The fpqc topology is defined on the category of schemes by specifying coverings as families of faithfully flat, quasi-compact morphisms that jointly surject onto the target scheme, ensuring the preservation of quasi-coherent sheaves under pullback. Unlike general Grothendieck topologies, which are abstractly defined via sieves satisfying axioms, the fpqc topology is concretely constructed to capture faithfully flat descent properties in algebraic geometry. This topology refines the fppf and fpqc topologies by focusing on morphisms that allow effective descent for quasi-coherent modules and algebraic structures.
Key Properties of the fpqc Topology
The fpqc topology is a Grothendieck topology on the category of schemes characterized by faithfully flat and quasi-compact morphisms that generate coverings. Key properties include stability under base change, meaning pullbacks of fpqc coverings are fpqc coverings, and effective descent for quasi-coherent sheaves, ensuring that descent data is effective for objects like modules and morphisms. This topology is finer than the fppf and etale topologies, making it essential for studying flat descent and faithfully flat descent in algebraic geometry.
Comparison with Other Grothendieck Topologies
The fpqc topology, defined by faithfully flat and quasi-compact morphisms, offers a finer coverage than many standard Grothendieck topologies such as the Zariski, etale, and fppf topologies by allowing more general morphisms. Unlike the etale topology, which restricts to unramified morphisms, fpqc topology accommodates faithfully flat morphisms that may have substantial ramification or non-local behavior. This increased generality enables fpqc to detect subtler cohomological phenomena and descent properties, positioning it as the finest among common Grothendieck topologies used in algebraic geometry.
Morphisms Relevant to fpqc and Grothendieck Sites
FPQC topology is defined using faithfully flat and quasi-compact morphisms, emphasizing coverings by morphisms that ensure descent of quasi-coherent sheaves and properties stable under base change. Grothendieck topology generalizes these concepts by specifying coverage via sieves or families of morphisms satisfying axioms abstracting open covers, often including fpqc coverings as particular cases. Morphisms relevant to fpqc sites typically feature flatness and quasi-compactness to guarantee effective descent, while Grothendieck sites accommodate a broader range of morphisms ensuring cohomological and sheaf-theoretic flexibility.
Sheaf Theory in fpqc vs Grothendieck Contexts
The fpqc topology, defined by faithfully flat and quasi-compact morphisms, provides a finer cover structure than general Grothendieck topologies, allowing for more flexible descent and sheaf conditions. Sheaf theory in the fpqc context emphasizes the ability to glue data over highly nontrivial flat covers, enabling effective handling of quasi-coherent sheaves and complex algebraic stacks. In contrast, Grothendieck topologies, like the etale or Zariski topologies, impose more restrictive locality conditions that simplify sheaf constructions but limit the generality of descent and cohomological analyses.
fpqc Topology: Strengths and Limitations
The fpqc topology excels in capturing faithfully flat quasi-compact morphisms, making it highly effective for descent theory and faithfully reflecting properties of schemes under base change. Its strength lies in ensuring epimorphic families for sheaf conditions, but its limitations include complexity and less intuitive geometric interpretation compared to Grothendieck topologies like the etale or Zariski topology. The Grothendieck topology framework generalizes various topologies, offering flexible coverage notions, whereas fpqc topology specifically focuses on flatness and quasi-compactness constraints, balancing generality and technical depth.
Applications of fpqc and Grothendieck Topologies
FPQC topology is essential in algebraic geometry for studying faithfully flat morphisms, enabling descent theory and effective treatment of quasi-coherent sheaves. Grothendieck topologies generalize classical topologies, allowing the development of etale, fppf, and fpqc topologies which facilitate cohomological methods and the formulation of stack theory. Applications of fpqc and Grothendieck topologies include the classification of algebraic stacks, descent of morphisms, and constructing moduli spaces with desirable geometric properties.
Conclusion: Choosing the Right Topology
FPQC topology excels in capturing faithfully flat and quasi-compact morphisms, making it ideal for descent theory and faithfully reflecting algebraic structures. Grothendieck topology, with its broader framework including Zariski, etale, and fppf topologies, provides more flexibility and is suited for various cohomological and sheaf-theoretic applications. Selecting the right topology depends on the specific geometric or algebraic problem, with FPQC favored for fine-grained flatness considerations and Grothendieck topologies for more general or flexible coverings.
fpqc topology Infographic
 libterm.com
libterm.com