A weak solution refers to a function that satisfies a differential equation in an integral or generalized sense rather than pointwise, allowing solutions where classical derivatives may not exist. This concept is crucial in partial differential equations and variational problems, extending the scope of solvable equations. Explore the rest of the article to deepen your understanding of weak solutions and their applications.
Table of Comparison
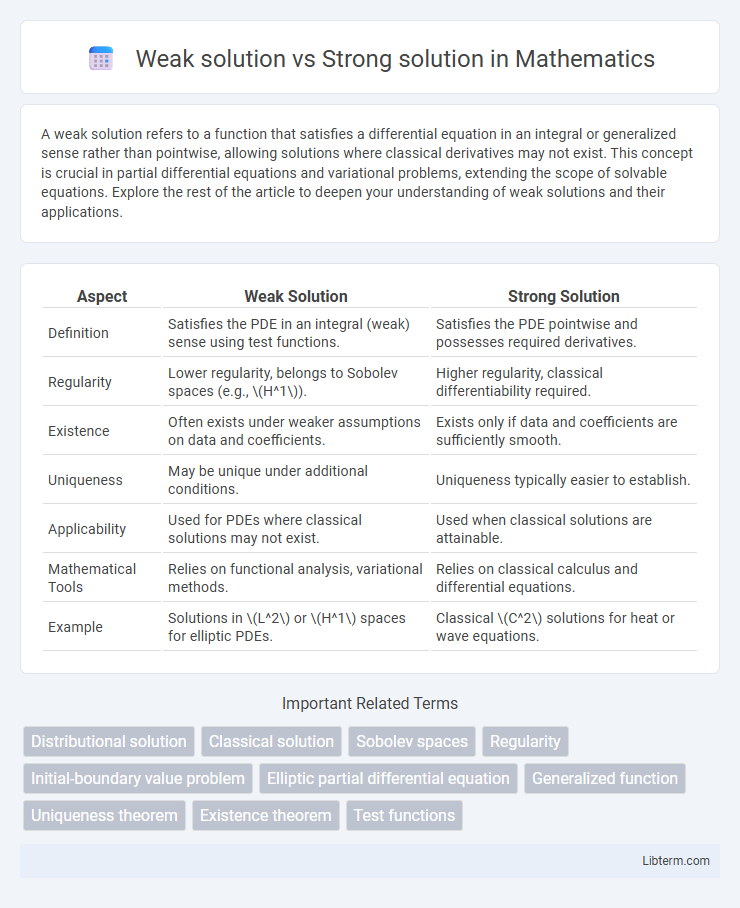
| Aspect | Weak Solution | Strong Solution |
|---|---|---|
| Definition | Satisfies the PDE in an integral (weak) sense using test functions. | Satisfies the PDE pointwise and possesses required derivatives. |
| Regularity | Lower regularity, belongs to Sobolev spaces (e.g., \(H^1\)). | Higher regularity, classical differentiability required. |
| Existence | Often exists under weaker assumptions on data and coefficients. | Exists only if data and coefficients are sufficiently smooth. |
| Uniqueness | May be unique under additional conditions. | Uniqueness typically easier to establish. |
| Applicability | Used for PDEs where classical solutions may not exist. | Used when classical solutions are attainable. |
| Mathematical Tools | Relies on functional analysis, variational methods. | Relies on classical calculus and differential equations. |
| Example | Solutions in \(L^2\) or \(H^1\) spaces for elliptic PDEs. | Classical \(C^2\) solutions for heat or wave equations. |
Introduction to Weak and Strong Solutions
Weak solutions allow partial differential equations to be satisfied in an integral or distributional sense, accommodating functions that may not possess traditional derivatives. Strong solutions require differentiability of the solution functions and satisfy the equations pointwise, reflecting classical interpretations. This distinction is fundamental in the analysis of PDEs where weak solutions broaden the scope for existence and uniqueness theorems.
Defining Weak Solutions
Weak solutions refer to functions that satisfy a differential equation in an integral or distributional sense rather than pointwise, allowing for less regularity and accommodating discontinuities or singularities. They are pivotal in partial differential equations, especially when classical or strong solutions do not exist due to lack of smoothness in data or coefficients. This concept extends solvability by interpreting derivatives weakly using test functions, enabling analysis in Sobolev spaces and ensuring broader applicability in mathematical physics and engineering models.
Defining Strong Solutions
Strong solutions to differential equations are functions that satisfy the equation pointwise and possess necessary derivatives as required by the equation's order, ensuring classical differentiability almost everywhere. These solutions typically lie within Sobolev spaces like \(H^1\) or \(H^2\), where the equation holds true in the classical sense. Defining strong solutions involves verifying existence, uniqueness, and regularity conditions that guarantee the function meets the differential operator constraints explicitly rather than in an integrated or distributional sense.
Mathematical Foundations
Weak solutions and strong solutions differ fundamentally in their mathematical foundations, particularly in the context of partial differential equations (PDEs). Strong solutions require classical differentiability and satisfy the PDEs pointwise, ensuring higher regularity and uniqueness under appropriate conditions. Weak solutions relax differentiability criteria by satisfying the PDEs in an integral or distributional sense, enabling analysis in broader function spaces such as Sobolev spaces and facilitating the study of existence when classical solutions may not exist.
Existence and Uniqueness Criteria
Weak solutions guarantee existence under broader conditions by relaxing differentiability requirements, making them suitable for PDEs with irregular data or domains. Strong solutions demand higher regularity, ensuring uniqueness and stability but exist only if initial and boundary data meet strict smoothness and compatibility criteria. Existence and uniqueness of weak solutions are often established via energy methods and compactness, whereas strong solutions rely on classical PDE theory and fixed-point arguments.
Regularity and Smoothness of Solutions
Weak solutions allow for functions with lower regularity, typically residing in Sobolev spaces like \( H^1 \) or \( L^2 \), accommodating discontinuities or singularities, whereas strong solutions require higher smoothness, often demanding continuous second derivatives or membership in \( C^1 \) or \( H^2 \) spaces. The differentiability and integrability conditions for strong solutions enable pointwise satisfaction of differential equations, while weak solutions satisfy them in an integral or distributional sense, granting existence under less restrictive smoothness assumptions. Regularity theory investigates conditions under which weak solutions gain additional smoothness, bridging the gap between weak and strong formulations in PDE analysis.
Application Areas in Differential Equations
Weak solutions are primarily applied in fluid dynamics, elasticity, and problems involving discontinuities or irregular domains where classical differentiability fails. Strong solutions are utilized in well-posed problems with smooth data, such as heat conduction, classical mechanics, and chemical reaction models, where uniqueness and stability are crucial. Numerical methods and finite element analysis often rely on weak solutions to handle complex boundary conditions and non-smooth phenomena efficiently.
Advantages and Limitations
A strong solution to a differential equation requires the function to be differentiable and satisfy the equation pointwise, offering precise and classical interpretations with clear physical meaning. Weak solutions relax regularity requirements, allowing functions that may not be differentiable everywhere but still satisfy the equation in an integral or distributional sense, enabling treatment of problems with discontinuities or singularities. While strong solutions provide detailed local behavior, they are limited to smooth data, and weak solutions extend applicability to broader function spaces but may lack uniqueness or finer properties.
Common Examples and Case Studies
Weak solutions frequently appear in fluid dynamics, particularly in modeling shock waves in Euler equations where discontinuities prevent classical solutions. Strong solutions are common in heat conduction problems governed by the heat equation, ensuring differentiability and uniqueness under smooth initial conditions. Case studies like the Navier-Stokes equations highlight the distinction: weak solutions exist globally but may lack regularity, while strong solutions exist locally with higher regularity, illustrating challenges in mathematical physics and PDE analysis.
Conclusion and Future Perspectives
Weak solutions provide broader applicability in solving partial differential equations, especially when classical solutions are unattainable due to irregularities or discontinuities. Strong solutions offer greater regularity and uniqueness but require more stringent conditions on the initial data and equations. Future research aims to bridge the gap between weak and strong solutions by developing improved regularity criteria and numerical methods to verify uniqueness and stability in complex systems.
Weak solution Infographic
 libterm.com
libterm.com