Lie algebra is a fundamental mathematical structure used to study continuous symmetries and their properties, playing a crucial role in fields such as theoretical physics, geometry, and representation theory. It consists of a vector space equipped with a binary operation called the Lie bracket, which satisfies specific antisymmetry and Jacobi identity conditions. Discover how Lie algebra can deepen your understanding of symmetry and its applications by exploring the rest of the article.
Table of Comparison
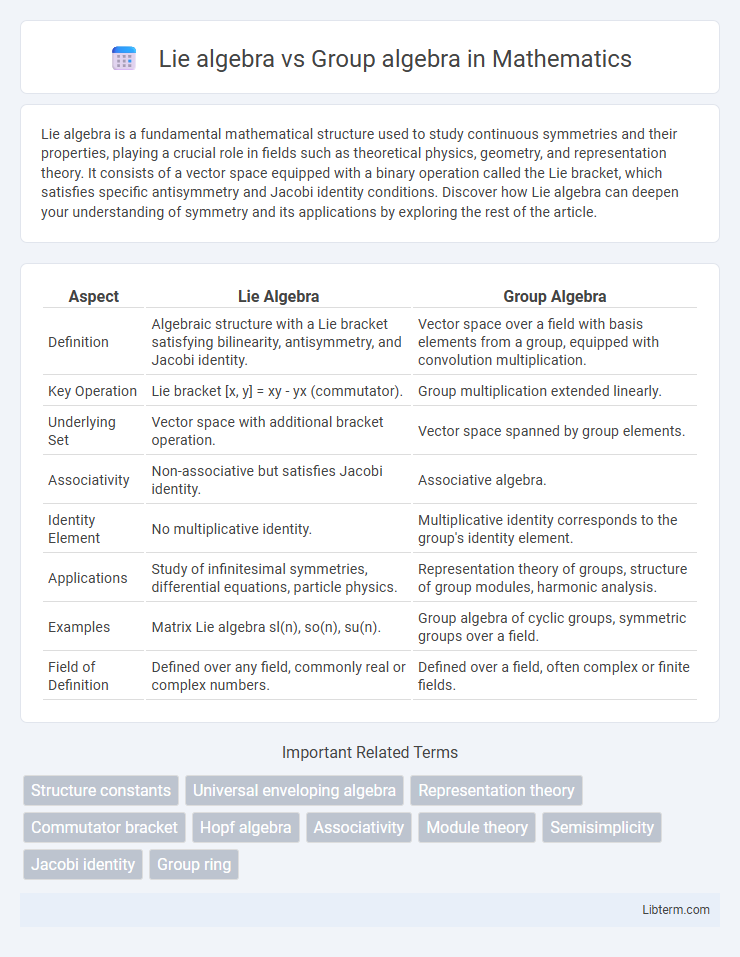
| Aspect | Lie Algebra | Group Algebra |
|---|---|---|
| Definition | Algebraic structure with a Lie bracket satisfying bilinearity, antisymmetry, and Jacobi identity. | Vector space over a field with basis elements from a group, equipped with convolution multiplication. |
| Key Operation | Lie bracket [x, y] = xy - yx (commutator). | Group multiplication extended linearly. |
| Underlying Set | Vector space with additional bracket operation. | Vector space spanned by group elements. |
| Associativity | Non-associative but satisfies Jacobi identity. | Associative algebra. |
| Identity Element | No multiplicative identity. | Multiplicative identity corresponds to the group's identity element. |
| Applications | Study of infinitesimal symmetries, differential equations, particle physics. | Representation theory of groups, structure of group modules, harmonic analysis. |
| Examples | Matrix Lie algebra sl(n), so(n), su(n). | Group algebra of cyclic groups, symmetric groups over a field. |
| Field of Definition | Defined over any field, commonly real or complex numbers. | Defined over a field, often complex or finite fields. |
Introduction to Lie Algebra and Group Algebra
Lie algebras are algebraic structures used to study continuous symmetries through elements that satisfy the Lie bracket, an antisymmetric bilinear operation encoding the infinitesimal structure of Lie groups. Group algebras combine group theory and ring theory by associating a vector space over a field with basis elements corresponding to a group, enabling algebraic manipulation of group elements. Understanding the relationship between Lie algebras and group algebras is fundamental in representation theory, where Lie algebras often arise as tangent spaces to Lie groups and group algebras assist in analyzing discrete group representations.
Fundamental Concepts and Definitions
Lie algebra is a vector space equipped with a bilinear, antisymmetric bracket operation satisfying the Jacobi identity, playing a central role in studying continuous symmetries and differentiable groups. Group algebra is an associative algebra constructed from a group and a base field, where group elements form a basis and multiplication extends linearly, serving as a framework for analyzing group representations. Both structures link algebraic properties to symmetry, with Lie algebras emphasizing infinitesimal transformations and group algebras focusing on discrete group elements.
Structural Differences Between Lie Algebra and Group Algebra
Lie algebras are algebraic structures characterized by a bilinear, antisymmetric Lie bracket satisfying the Jacobi identity, which governs their behavior as infinitesimal generators of continuous symmetry groups. Group algebras, constructed from a group and a field, form associative algebras where the group elements serve as a basis, enabling representation theory through linear combinations and convolution-like multiplication. The core structural difference lies in Lie algebras embodying non-associative operations focused on infinitesimal transformations, whereas group algebras emphasize associative multiplication reflecting global group structures.
Algebraic Operations and Properties
Lie algebras feature a bilinear, antisymmetric Lie bracket operation satisfying the Jacobi identity, which defines the structure and governs algebraic manipulations within the algebra. Group algebras are constructed by extending group elements linearly over a field, where multiplication inherits the group's operation but is associative and typically non-commutative. The core distinction lies in Lie algebras encoding infinitesimal symmetries through brackets, while group algebras provide a richer associative framework encapsulating entire group structures algebraically.
Representation Theory Comparison
Representation theory of Lie algebras primarily studies linear actions on vector spaces via Lie algebra homomorphisms, highlighting structures like weights and root systems, while group algebra representations involve modules over the group algebra, connecting the group's structure with linear transformations. Lie algebra representations are often infinite-dimensional and involve continuous symmetries, whereas group algebra representations are generally finite-dimensional and relate to discrete symmetries. Both frameworks use module theory, but Lie algebra representations provide tools for differential geometric applications, and group algebra representations emphasize combinatorial and character-theoretic aspects.
Applications in Mathematics and Physics
Lie algebras, fundamental in studying continuous symmetries, play a crucial role in differential geometry, quantum mechanics, and particle physics by describing infinitesimal transformations and conserved quantities. Group algebras provide algebraic frameworks for representing finite groups, facilitating the analysis of symmetry properties in crystallography, coding theory, and harmonic analysis. Both structures enable the examination of symmetry through algebraic methods, with Lie algebras focusing on continuous groups and group algebras on discrete groups, impacting representation theory and the classification of elementary particles.
Examples of Lie Algebras and Group Algebras
Lie algebras, such as the algebra of \( n \times n \) skew-symmetric matrices or the Heisenberg algebra, capture the infinitesimal structure of continuous transformation groups and are fundamental in differential geometry and theoretical physics. Group algebras, exemplified by the group algebra \( \mathbb{C}[G] \) of a finite group \( G \), form associative algebras that encode group operations algebraically and are critical in representation theory. The Lie algebra \( \mathfrak{sl}_2(\mathbb{R}) \) and the group algebra of the symmetric group \( S_n \) illustrate the distinct algebraic frameworks and applications of these two structures.
Importance in Modern Algebraic Research
Lie algebras provide a fundamental framework for studying infinitesimal symmetries and continuous transformation groups, playing a crucial role in differential geometry and theoretical physics. Group algebras enable algebraic encoding of group symmetries through linear combinations of group elements, facilitating representation theory and module analysis. Their interplay advances modern algebraic research by linking structural insights of symmetry groups with linear operator techniques, impacting quantum mechanics, number theory, and algebraic topology.
Interconnections and Interplay
Lie algebra and group algebra are deeply interconnected through the exponential map, which bridges Lie algebras with Lie groups, enabling the translation of algebraic structures into group-theoretic contexts. The universal enveloping algebra of a Lie algebra plays a critical role in representing Lie algebras within group algebras, facilitating the study of representations and harmonic analysis on groups. This interplay allows for a comprehensive understanding of symmetry and transformation in both continuous and discrete settings within mathematics and theoretical physics.
Summary and Future Directions
Lie algebras and group algebras serve distinct roles in algebraic structures, with Lie algebras capturing infinitesimal symmetries through bracket operations, while group algebras provide a framework to study group representations via associative algebra structures. Future research is poised to explore deeper interconnections, particularly in quantum group theory, categorical algebra, and applications to mathematical physics, where hybrid approaches may yield novel algebraic insights. Advances in computational methods and homological techniques are expected to enhance the understanding of representation theory and deformation quantization in these algebraic contexts.
Lie algebra Infographic
 libterm.com
libterm.com