Homeomorphism is a fundamental concept in topology describing a continuous, bijective mapping between two spaces with a continuous inverse, indicating they are topologically equivalent. Understanding homeomorphisms helps classify spaces based on their intrinsic properties, rather than their exact geometric shape. Explore the rest of the article to deepen your knowledge of how homeomorphisms reveal the nature of geometric spaces.
Table of Comparison
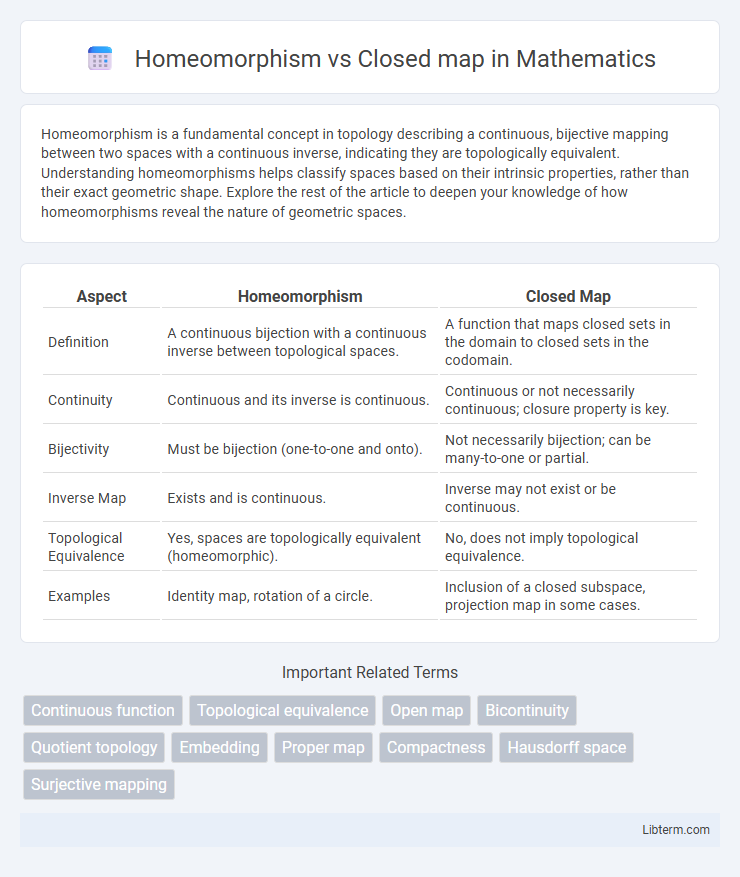
| Aspect | Homeomorphism | Closed Map |
|---|---|---|
| Definition | A continuous bijection with a continuous inverse between topological spaces. | A function that maps closed sets in the domain to closed sets in the codomain. |
| Continuity | Continuous and its inverse is continuous. | Continuous or not necessarily continuous; closure property is key. |
| Bijectivity | Must be bijection (one-to-one and onto). | Not necessarily bijection; can be many-to-one or partial. |
| Inverse Map | Exists and is continuous. | Inverse may not exist or be continuous. |
| Topological Equivalence | Yes, spaces are topologically equivalent (homeomorphic). | No, does not imply topological equivalence. |
| Examples | Identity map, rotation of a circle. | Inclusion of a closed subspace, projection map in some cases. |
Introduction to Homeomorphism and Closed Map
A homeomorphism is a continuous bijection between topological spaces with a continuous inverse, preserving topological properties and enabling the spaces to be considered topologically equivalent. A closed map is a function between topological spaces that maps closed sets to closed sets, which plays a critical role in maintaining closure properties under the mapping. Understanding the distinctions and relationships between homeomorphisms and closed maps is fundamental in topology for classifying spaces and analyzing continuity and closure behavior.
Defining Homeomorphism in Topology
A homeomorphism in topology is a continuous bijection between two topological spaces with a continuous inverse, ensuring a perfect topological equivalence. Unlike closed maps, which only require the image of closed sets to be closed, a homeomorphism preserves both open and closed set structures through invertible mappings. This bijective correspondence maintains topological properties such as connectedness and compactness, making homeomorphisms fundamental in classifying spaces up to topological equivalence.
Understanding Closed Maps: A Formal Definition
A closed map is a function between topological spaces that maps every closed set in the domain to a closed set in the codomain, preserving the closure property under continuous mappings. Unlike homeomorphisms, which require bijectivity and continuous inverses, closed maps emphasize the topological closure without necessarily being invertible or open. Understanding closed maps involves recognizing their role in continuity and topology preservation, crucial for analyzing limits, compactness, and boundary behavior in mathematical structures.
Key Properties of Homeomorphisms
Homeomorphisms are continuous bijections with continuous inverses, preserving topological properties such as openness, closedness, and connectedness between spaces. Unlike closed maps, which only guarantee the image of closed sets remains closed, homeomorphisms ensure a perfect topological equivalence by maintaining both open and closed set structures. Key properties include preserving compactness, Hausdorff conditions, and neighborhood bases, making homeomorphisms fundamental in classifying topological spaces.
Essential Features of Closed Maps
Closed maps are functions between topological spaces that send closed sets to closed sets, ensuring the preservation of closure properties in the target space. Unlike homeomorphisms, which require a bijective, continuous function with a continuous inverse guaranteeing a topological equivalence, closed maps do not necessarily preserve open sets or bijectivity. The essential feature of closed maps is their capacity to maintain closedness under image, playing a crucial role in identifying quotient spaces and ensuring continuity with respect to closed structures.
Homeomorphism vs Closed Map: Core Differences
Homeomorphisms are continuous bijections with continuous inverses, guaranteeing topological equivalence between spaces, whereas closed maps only require the image of closed sets to be closed without necessarily being bijections or inverses. The core difference lies in homeomorphisms preserving topological structure fully, while closed maps merely ensure the preservation of closedness in images, lacking the inverse continuity constraint. Understanding these distinctions is crucial for analyzing when spaces are topologically identical versus when only closure properties are maintained under a mapping.
Examples Illustrating Homeomorphisms
Homeomorphisms are continuous bijections with continuous inverses, exemplified by the mapping of a circle onto an ellipse, preserving topological properties. In contrast, closed maps send closed sets to closed sets without requiring bijectivity or inverse continuity, such as the projection from a cylinder to a circle. Understanding homeomorphisms through examples like the deformation of a coffee cup into a donut highlights their role in topology, unlike closed maps which emphasize set-theoretic closure properties.
Examples of Closed Maps in Practice
Closed maps occur frequently in topology and analysis, with classic examples including quotient maps and continuous surjections from compact spaces onto Hausdorff spaces. The projection map from a product space onto one of its factors is another important example, as it carries closed sets onto closed sets. Unlike homeomorphisms, which require bijective continuous maps with continuous inverses, closed maps preserve closedness without necessarily being invertible or open.
Importance of Homeomorphisms and Closed Maps in Topology
Homeomorphisms are crucial in topology as they define when two spaces are topologically equivalent, preserving properties such as continuity and neighborhood structures. Closed maps ensure that the image of a closed set remains closed, playing a key role in understanding continuity and compactness. Together, homeomorphisms and closed maps help classify spaces and analyze their intrinsic topological properties.
Conclusion: Choosing Between Homeomorphism and Closed Map
Choosing between a homeomorphism and a closed map depends on the desired topological properties and the level of structural preservation required. Homeomorphisms guarantee a bicontinuous bijection preserving topological equivalence and all properties of the spaces, making them ideal for identifying spaces as topologically identical. Closed maps ensure image sets remain closed but may not preserve topological equivalence or invertibility, thus serving well in specific continuity contexts without enforcing full homeomorphic structure.
Homeomorphism Infographic
 libterm.com
libterm.com