Jordan algebra is a nonassociative algebraic structure primarily studied in abstract algebra and mathematical physics, characterized by a commutative product satisfying the Jordan identity. This concept plays a significant role in quantum mechanics and projective geometry, providing a framework for understanding observables and symmetries. Explore the rest of the article to uncover how Jordan algebras impact modern mathematical theories and applications.
Table of Comparison
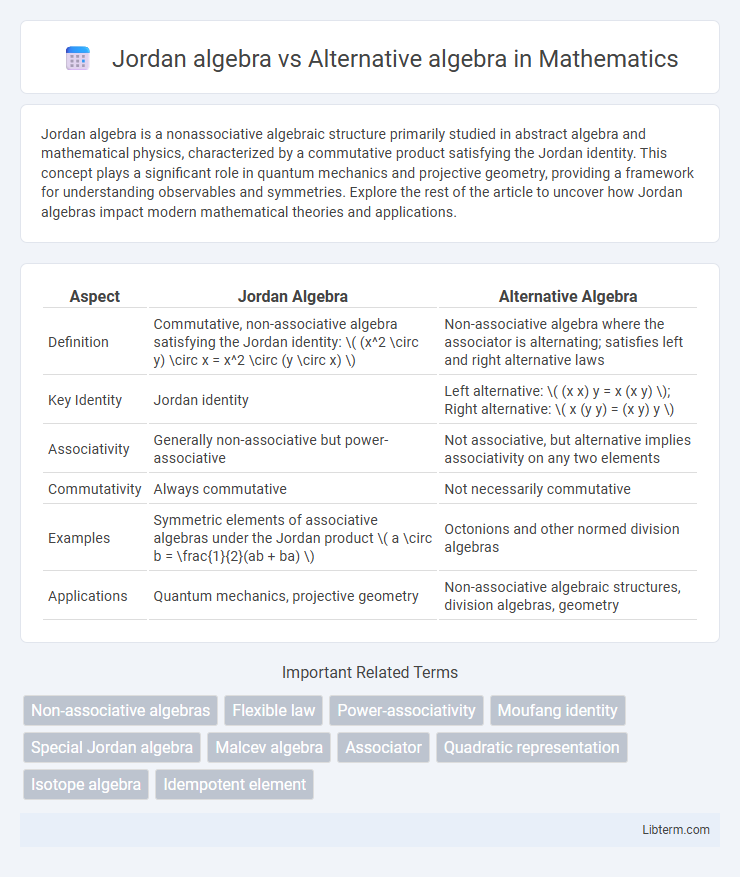
| Aspect | Jordan Algebra | Alternative Algebra |
|---|---|---|
| Definition | Commutative, non-associative algebra satisfying the Jordan identity: \( (x^2 \circ y) \circ x = x^2 \circ (y \circ x) \) | Non-associative algebra where the associator is alternating; satisfies left and right alternative laws |
| Key Identity | Jordan identity | Left alternative: \( (x x) y = x (x y) \); Right alternative: \( x (y y) = (x y) y \) |
| Associativity | Generally non-associative but power-associative | Not associative, but alternative implies associativity on any two elements |
| Commutativity | Always commutative | Not necessarily commutative |
| Examples | Symmetric elements of associative algebras under the Jordan product \( a \circ b = \frac{1}{2}(ab + ba) \) | Octonions and other normed division algebras |
| Applications | Quantum mechanics, projective geometry | Non-associative algebraic structures, division algebras, geometry |
Introduction to Jordan and Alternative Algebras
Jordan algebras are non-associative algebras defined by the Jordan identity (x2 * y) * x = x2 * (y * x), emphasizing commutative multiplication and applications in quantum mechanics and projective geometry. Alternative algebras generalize associative algebras by satisfying the left and right alternative laws (x * x) * y = x * (x * y) and y * (x * x) = (y * x) * x, playing a key role in the study of composition algebras and octonions. Both structures extend classical algebraic systems while relaxing associativity constraints, enabling exploration of symmetries and invariants in mathematics and physics.
Historical Background and Development
Jordan algebras originated in the 1930s through the work of Pascual Jordan, who aimed to formalize algebraic structures underlying quantum mechanics. Alternative algebras, developed earlier in the early 20th century by mathematicians like A.A. Albert, generalize associative algebras by relaxing associativity conditions to alternative laws. Both algebra types played significant roles in the evolution of non-associative algebraic systems, influencing modern mathematical physics and abstract algebra research.
Fundamental Definitions and Concepts
Jordan algebras are non-associative algebras defined by the commutative Jordan product \(a \circ b = \frac{1}{2}(ab + ba)\) and satisfy the Jordan identity \((a^2 \circ b) \circ a = a^2 \circ (b \circ a)\). Alternative algebras, characterized by the alternative laws \((aa)b = a(ab)\) and \(a(bb) = (ab)b\), generalize associative algebras by allowing non-associative multiplication while preserving left and right alternativity. The fundamental difference lies in Jordan algebras focusing on commutativity and a specific polynomial identity, whereas alternative algebras emphasize weaker forms of associativity through alternative identities.
Key Properties of Jordan Algebras
Jordan algebras are commutative algebras characterized by the Jordan identity: \( (x^2 \circ y) \circ x = x^2 \circ (y \circ x) \), ensuring power-associativity and symmetrization of associative products. Unlike alternative algebras, which satisfy the alternative laws and are generally noncommutative but flexible, Jordan algebras emphasize commutativity and a special form of associativity that arises from symmetrized associative multiplication. These properties enable Jordan algebras to model observables in quantum mechanics and possess rich algebraic structures distinct from the non-associative but alternative frameworks.
Key Properties of Alternative Algebras
Alternative algebras are characterized by the flexibility of their multiplication, satisfying the left and right alternative laws, which imply that the subalgebra generated by any two elements is associative. Unlike Jordan algebras, which are commutative and satisfy the Jordan identity, alternative algebras need not be commutative but maintain associativity in any two-element subalgebra. Key properties include the associator's alternation, meaning the associator vanishes whenever two arguments are equal, ensuring that the multiplication is "almost associative" and allowing the construction of important algebraic structures like octonions.
Structural Differences Between Jordan and Alternative Algebras
Jordan algebras are commutative but not necessarily associative, characterized by the Jordan identity (a2 b) a = a2 (b a), which distinguishes their multiplication structure. Alternative algebras maintain a weaker associativity condition through the alternative laws, where the associator (a, a, b) and (b, a, a) vanish, ensuring any two elements generate an associative subalgebra. Structural differences manifest as Jordan algebras emphasize symmetric product operations with power-associativity, while alternative algebras generalize associativity by relaxing it but preserving the alternativity condition, often enabling noncommutative multiplication.
Examples and Applications in Mathematics and Physics
Jordan algebras, exemplified by the algebra of self-adjoint operators on a Hilbert space with the Jordan product, are extensively used in quantum mechanics to model observables and study quantum states, while alternative algebras, such as the octonions, play a critical role in understanding non-associative structures in algebra and appear in certain physical theories like string theory and special relativity. Applications of Jordan algebras in mathematics include the classification of formally real Jordan algebras and symmetries in projective geometry, whereas alternative algebras find applications in the construction of division algebras and exceptional Lie groups. The distinction between these algebraic structures lies in their underlying identities: Jordan algebras satisfy the Jordan identity ensuring commutativity in their product, while alternative algebras satisfy weaker associativity conditions, allowing for more generalized non-associative compositions.
Comparison of Associativity and Commutativity
Jordan algebras are commutative but generally non-associative, characterized by the Jordan identity (a2*b)*a = a2*(b*a), ensuring a weakened form of associativity suited for quantum mechanics. Alternative algebras are non-commutative but satisfy the alternative laws, meaning the associator vanishes when two arguments are identical, providing a partial associativity stronger than that in Jordan algebras. The key distinction lies in Jordan algebras emphasizing commutativity with weak associativity constraints, while alternative algebras relax commutativity but impose alternative associativity conditions.
Roles in Modern Algebraic Research
Jordan algebras play a critical role in the study of non-associative algebras with applications in quantum mechanics and projective geometry, emphasizing commutative but non-associative operations. Alternative algebras, characterized by the alternativity property, extend associative algebra frameworks and contribute to division algebra theory, particularly in octonion and Cayley algebra research. Both algebraic structures enrich modern algebraic research by enabling exploration of symmetry, structural classification, and applications in theoretical physics and geometry.
Summary and Future Directions
Jordan algebras, characterized by their commutative but non-associative product satisfying the Jordan identity, find applications in quantum mechanics and projective geometry, while alternative algebras generalize associative algebras by relaxing associativity only on certain elements, notably including octonions. Comparative studies highlight Jordan algebras' relevance in symmetric cone theory and special relativity, whereas alternative algebras underpin exceptional Lie groups and non-associative division algebras. Future research directions aim to deepen the understanding of automorphism groups, explore applications in theoretical physics, and develop classification frameworks integrating both algebraic structures in unified non-associative algebra systems.
Jordan algebra Infographic
 libterm.com
libterm.com