Understanding the intricacies of the field enhances your ability to navigate challenges and leverage opportunities effectively. Mastery of key concepts and skills ensures meaningful contributions and career advancement. Explore the rest of the article to discover essential insights and strategies for success in your field.
Table of Comparison
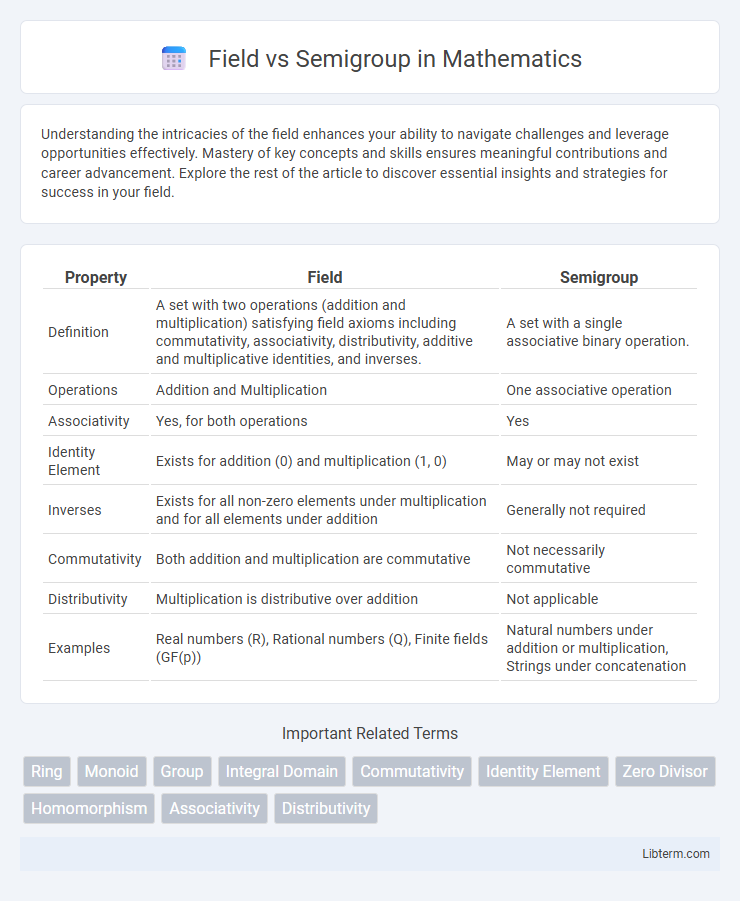
| Property | Field | Semigroup |
|---|---|---|
| Definition | A set with two operations (addition and multiplication) satisfying field axioms including commutativity, associativity, distributivity, additive and multiplicative identities, and inverses. | A set with a single associative binary operation. |
| Operations | Addition and Multiplication | One associative operation |
| Associativity | Yes, for both operations | Yes |
| Identity Element | Exists for addition (0) and multiplication (1, 0) | May or may not exist |
| Inverses | Exists for all non-zero elements under multiplication and for all elements under addition | Generally not required |
| Commutativity | Both addition and multiplication are commutative | Not necessarily commutative |
| Distributivity | Multiplication is distributive over addition | Not applicable |
| Examples | Real numbers (R), Rational numbers (Q), Finite fields (GF(p)) | Natural numbers under addition or multiplication, Strings under concatenation |
Introduction to Algebraic Structures
Fields and semigroups are fundamental algebraic structures with distinct properties crucial in abstract algebra. A field is a set equipped with two operations, addition and multiplication, where every nonzero element has a multiplicative inverse, enabling division. In contrast, a semigroup requires only one associative binary operation without necessarily having identity or inverse elements, making fields richer structures used widely in algebraic systems and number theory.
Defining Fields: Core Concepts
A field is an algebraic structure consisting of a set equipped with two operations: addition and multiplication, where both operations are associative, commutative, and have identity elements, along with additive inverses and multiplicative inverses for all non-zero elements. Fields satisfy distributivity, linking addition and multiplication, which contrasts with semigroups that only require an associative binary operation without necessarily having identities or inverses. Core concepts defining fields include the presence of identity elements (0 for addition, 1 for multiplication), additive inverses for every element, and multiplicative inverses for every non-zero element, ensuring a rich algebraic framework for solving equations and performing division.
Understanding Semigroups: Basic Properties
A semigroup is an algebraic structure consisting of a non-empty set equipped with an associative binary operation, ensuring closure within the set. Unlike fields, semigroups do not require the existence of identity elements or inverses, focusing instead on the fundamental property of associativity. This foundational concept underpins more complex structures such as monoids and groups, highlighting the incremental nature of algebraic hierarchy.
Key Differences Between Fields and Semigroups
Fields are algebraic structures equipped with two operations, addition and multiplication, where every nonzero element has a multiplicative inverse, ensuring the existence of division. Semigroups consist of a single associative binary operation without requiring identity or inverse elements, making their structure less restrictive than fields. The key difference lies in fields supporting both addition and multiplication with inverses and identities, while semigroups only require closure and associativity under one operation.
Examples of Fields in Mathematics
Fields in mathematics include the set of rational numbers (Q), real numbers (R), and complex numbers (C), all of which support addition, subtraction, multiplication, and division operations except division by zero. These sets satisfy field axioms such as associativity, commutativity, distributivity, and the existence of additive and multiplicative inverses. Unlike semigroups, which only require closure and associativity under a single binary operation, fields form richer algebraic structures enabling advanced mathematical analysis and applications.
Examples of Semigroups in Practice
Semigroups are algebraic structures consisting of a set equipped with an associative binary operation, commonly seen in examples like strings under concatenation, natural numbers with addition, or square matrices under multiplication. Unlike fields, semigroups do not require elements to have inverses or identity elements, which broadens their applicability in computer science and abstract algebra. Practical instances include modeling state transitions in automata, combining logging events in software development, and representing non-negative weight combinations in graph theory.
Algebraic Operations: What Sets Fields Apart
Fields exhibit two binary operations, addition and multiplication, each forming an abelian group with the multiplicative group excluding zero. Semigroups have only one associative binary operation without requiring identity or inverses, unlike fields that demand multiplicative inverses for all nonzero elements. The presence of distributive laws in fields further distinguishes them by linking addition and multiplication into a cohesive algebraic structure.
Applications of Fields and Semigroups
Fields are essential in cryptography, coding theory, and signal processing due to their well-defined addition, multiplication, and inverses enabling complex arithmetic operations. Semigroups find applications in computer science, automata theory, and formal language processing by modeling state transitions and combining discrete elements without requiring inverses. The algebraic structures of fields support error correction and secure communication, while semigroups facilitate optimization in concurrent systems and data aggregation tasks.
Comparing Field Axioms vs Semigroup Axioms
Field axioms require two binary operations, addition and multiplication, each forming abelian groups under their respective operations, with multiplication distributive over addition, while semigroup axioms involve a single associative binary operation without necessitating identity or inverses. Unlike semigroups, fields mandate additive and multiplicative identities, additive inverses for all elements, and multiplicative inverses for all nonzero elements, ensuring richer algebraic structure. The distributive law is fundamental in fields but absent in semigroup axioms, highlighting the complexity and hierarchy between these algebraic systems.
Conclusion: Choosing Between Field and Semigroup
Choosing between a field and a semigroup depends on the algebraic properties required for a specific application. Fields provide a rich structure with both additive and multiplicative inverses, enabling division and extensive manipulation in linear algebra and calculus. Semigroups offer simpler, associative operations without the necessity of inverses, making them suitable for modeling processes like string concatenation or state transitions where invertibility is not essential.
Field Infographic
 libterm.com
libterm.com