Inverse operations are fundamental in mathematics, enabling you to reverse a calculation or solve equations efficiently. Understanding how functions, matrices, and numbers interact through their inverses enhances problem-solving skills and deepens comprehension of algebraic structures. Explore the rest of this article to discover practical examples and applications of inverse concepts in various fields.
Table of Comparison
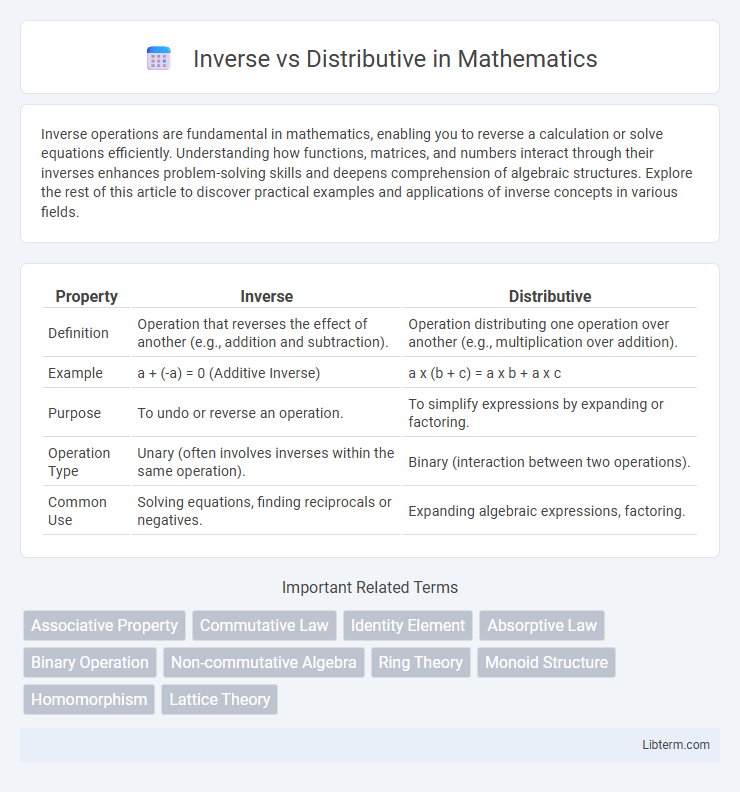
| Property | Inverse | Distributive |
|---|---|---|
| Definition | Operation that reverses the effect of another (e.g., addition and subtraction). | Operation distributing one operation over another (e.g., multiplication over addition). |
| Example | a + (-a) = 0 (Additive Inverse) | a x (b + c) = a x b + a x c |
| Purpose | To undo or reverse an operation. | To simplify expressions by expanding or factoring. |
| Operation Type | Unary (often involves inverses within the same operation). | Binary (interaction between two operations). |
| Common Use | Solving equations, finding reciprocals or negatives. | Expanding algebraic expressions, factoring. |
Introduction to Inverse and Distributive Properties
The inverse property involves operations that undo each other, such as addition and subtraction or multiplication and division, resulting in the original value, like a + (-a) = 0 or a x (1/a) = 1. The distributive property allows multiplication to be distributed over addition or subtraction within parentheses, illustrated by a(b + c) = ab + ac. Understanding these properties is fundamental in simplifying algebraic expressions and solving equations efficiently.
Definition of Inverse Property
The inverse property in mathematics states that for every element, there exists another element that combines with it to yield the identity element, such as in addition where a number plus its additive inverse equals zero. The distributive property involves multiplying a sum by distributing the multiplier to each term inside the parentheses. Understanding the inverse property is essential for solving equations and simplifying expressions by reversing operations.
Definition of Distributive Property
The distributive property defines how multiplication interacts with addition or subtraction, stating that a(b + c) equals ab + ac. This property allows for the multiplication of each addend within a parenthesis by a single factor outside, facilitating simpler algebraic expressions. Inverse operations, in contrast, involve reversing the effect of an operation, such as subtraction undoing addition.
Mathematical Representation of Inverse
The mathematical representation of inverse typically involves finding a value or function that reverses the effect of an original operation, such as the inverse of a function \(f(x)\) denoted by \(f^{-1}(x)\), where \(f(f^{-1}(x)) = x\). In contrast, the distributive property relates to the multiplication of a number over addition or subtraction, expressed as \(a(b + c) = ab + ac\). Understanding these representations highlights how inverse operations undo processes while distributive operations distribute terms across sums or differences.
Mathematical Representation of Distributive
The distributive property in mathematics is represented by the equation a(b + c) = ab + ac, demonstrating how multiplication distributes over addition. This property allows the expansion of expressions by multiplying a single term by each term inside a parenthesis. In contrast, inverse operations like addition and subtraction or multiplication and division reverse each other, but do not involve distribution across terms.
Key Differences Between Inverse and Distributive
The inverse property involves finding a value that, when combined with the original number, results in the identity element, such as a + (-a) = 0 for addition or a x (1/a) = 1 for multiplication. The distributive property describes how multiplication distributes over addition or subtraction: a x (b + c) = a x b + a x c, emphasizing the expansion of expressions. Key differences include that the inverse property relates to operations that undo each other to yield an identity, while the distributive property focuses on how one operation distributes over another within an expression.
Practical Applications in Algebra
Inverse and distributive properties serve distinct roles in algebraic problem-solving: the inverse property, involving operations like addition and multiplication, helps simplify equations by reversing quantities to isolate variables, essential in solving linear equations and checking solutions. The distributive property expands expressions by multiplying a single term across terms inside parentheses, crucial in simplifying polynomials, factoring, and solving equations efficiently. Mastery of these properties enhances manipulation of algebraic expressions, leading to clearer steps in equation solving and improved mathematical reasoning.
Common Errors and Misconceptions
Common errors in understanding inverse and distributive properties often involve confusing the operations; the inverse property relates to adding or multiplying by a number's opposite to yield an identity element, while the distributive property involves multiplying a sum by distributing the multiplication over each addend. A typical misconception is assuming that the distributive property applies to division or that the inverse operation can be applied without context, leading to incorrect simplifications. Misapplication of these properties results in errors such as treating subtraction as distributive or using inverses incorrectly in equations.
Importance in Problem Solving
The inverse property enables solving equations by reversing operations, essential for isolating variables and simplifying expressions in problem solving. The distributive property allows for expanding and factoring expressions, making complex problems more manageable by breaking them into smaller parts. Mastery of both properties enhances algebraic manipulation skills and improves accuracy in solving linear and quadratic equations.
Summary and Conclusion
Inverse and distributive properties serve distinct purposes in algebraic operations; the inverse property involves an element that reverses the effect of an operation, returning to the identity element, while the distributive property describes how multiplication distributes over addition or subtraction. Understanding these properties aids in simplifying expressions and solving equations effectively. Mastery of inverse and distributive properties enhances problem-solving skills and mathematical flexibility.
Inverse Infographic
 libterm.com
libterm.com