Ordinal numbers indicate position or rank in a sequential order, such as first, second, or third. They are essential in organizing data, events, or instructions where order matters more than quantity. Discover how understanding ordinals can improve your communication and clarity by reading the full article.
Table of Comparison
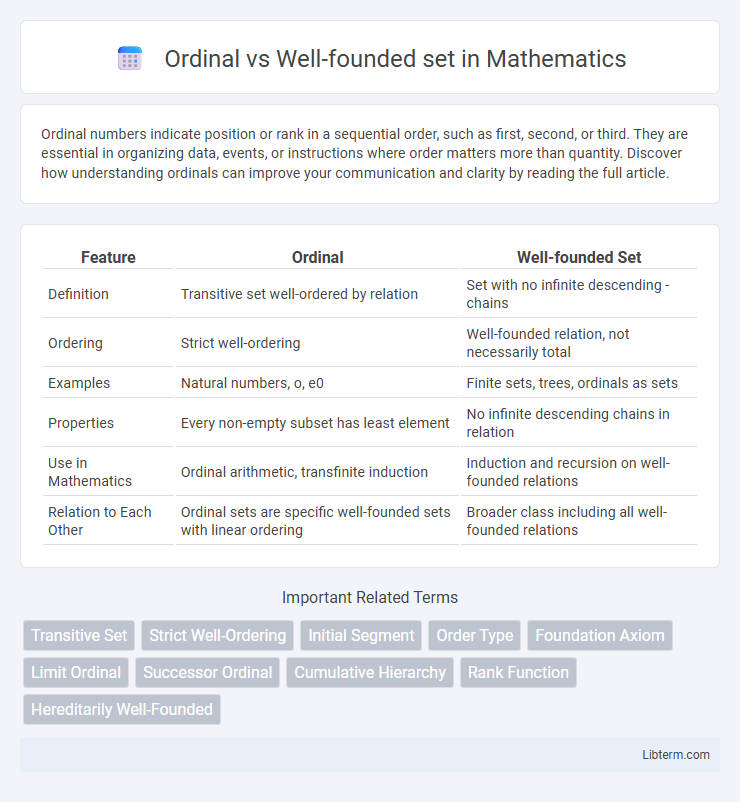
| Feature | Ordinal | Well-founded Set |
|---|---|---|
| Definition | Transitive set well-ordered by relation | Set with no infinite descending -chains |
| Ordering | Strict well-ordering | Well-founded relation, not necessarily total |
| Examples | Natural numbers, o, e0 | Finite sets, trees, ordinals as sets |
| Properties | Every non-empty subset has least element | No infinite descending chains in relation |
| Use in Mathematics | Ordinal arithmetic, transfinite induction | Induction and recursion on well-founded relations |
| Relation to Each Other | Ordinal sets are specific well-founded sets with linear ordering | Broader class including all well-founded relations |
Introduction to Ordinal and Well-founded Sets
Ordinal sets represent ordered types extending natural numbers to describe positions in well-ordered sequences, characterized by transfinite recursion and the principle of transfinite induction. Well-founded sets, defined by the absence of infinitely descending membership chains, ensure every non-empty subset has a minimal element, playing a crucial role in set theory and foundational mathematics. Both concepts underpin the structure of order types and support rigorous proofs involving induction and recursion over infinite sets.
Defining Ordinal Sets
Ordinal sets are defined through transfinite induction as well-ordered sets that are strictly well-ordered by membership, where each element is also an ordinal representing all smaller ordinals. These sets satisfy the property of being well-founded, meaning no infinite descending membership sequences exist, ensuring each non-empty subset has a least element. The concept of ordinals extends natural numbers into the transfinite by capturing order types of well-ordered sets and enabling rigorous handling of infinite hierarchies.
Understanding Well-founded Sets
Well-founded sets are defined by the absence of infinite descending membership chains, ensuring every non-empty subset has a minimal element, a property crucial for induction and recursion in set theory. Ordinal sets, as specific well-founded sets, are transitive and well-ordered by membership, representing order types of well-ordered sets. Understanding well-founded sets enables foundational insights into foundational mathematics, enabling proofs of termination and structural induction beyond ordinals.
Key Differences Between Ordinal and Well-founded Sets
Ordinal sets are transitive well-ordered sets where every element has a unique position in a strict well-ordering, enabling definition of order types. Well-founded sets are defined by the absence of infinitely descending membership chains, ensuring no infinite regression without requiring a total order. The key difference lies in ordinals possessing a linear, well-defined order structure, while well-founded sets only guarantee foundation without imposing total comparability among elements.
Properties of Ordinal Sets
Ordinal sets are transitive sets well-ordered by the membership relation , meaning every non-empty subset has a least element under . Each element of an ordinal set is also an ordinal, ensuring a strict linear order and enabling transfinite induction and recursion. Well-foundedness guarantees no infinite descending -chains, but ordinal sets specifically possess a well-ordering structure that distinguishes them within the class of well-founded sets.
Properties of Well-founded Sets
Well-founded sets are characterized by the absence of infinite descending sequences, ensuring every non-empty subset has a minimal element, which guarantees termination in recursive definitions. Unlike ordinals that are transitive and well-ordered by , well-founded sets may lack total comparability but still prohibit infinite regressions, emphasizing the foundational role in set theory. This property enables well-founded induction, essential for proofs and constructions across mathematical logic and computer science.
Applications in Set Theory
Ordinal numbers serve as fundamental tools in set theory for organizing well-ordered sets, enabling the classification of sets by their order type and supporting transfinite induction proofs. Well-founded sets, characterized by the absence of infinite descending membership chains, play a crucial role in defining rank functions and constructing cumulative hierarchies such as the von Neumann universe. Both concepts underpin large-scale set-theoretic constructions, including proofs of consistency and models of axiomatic systems like ZFC, facilitating the analysis of foundational properties and the development of recursive definitions.
Ordinal Sets in Hierarchical Structures
Ordinal sets serve as fundamental tools for representing hierarchical structures by providing a well-ordered framework where each element has a unique position. These sets enable the classification of levels or stages within complex hierarchies, supporting transfinite sequences that extend beyond finite boundaries. Their reliance on well-ordering ensures clear, unambiguous precedence, making them essential for modeling processes in mathematics, computer science, and logic.
The Role of Well-founded Sets in Proofs
Well-founded sets provide a foundational tool in proofs by ensuring no infinite descending chains exist, enabling induction and recursion principles crucial in set theory and logic. They underpin ordinal analysis by structuring ordinals as equivalence classes of well-ordered sets, facilitating transfinite induction. This property guarantees termination in recursive definitions and supports the construction of hierarchies in foundational mathematics.
Conclusion: Choosing Ordinals vs Well-founded Sets
Ordinals provide a structured, linear hierarchy ideal for indexing and well-ordering tasks, while well-founded sets emphasize the absence of infinite descending chains, ensuring foundational rigor in set theory. Selecting ordinals is advantageous when a clear, transfinite sequence is needed, whereas well-founded sets offer broader applicability in modeling inductive definitions and recursive constructions. The choice depends on whether the focus is on linear order properties or foundational guarantees against infinite descent.
Ordinal Infographic
 libterm.com
libterm.com